[Paper 리뷰] PVAE-TTS: Adaptive Text-to-Speech via Progressive Style Adaptation

PVAE-TTS: Adaptive Text-to-Speech via Progressive Style Adaptation

---

• Adaptive text-to-speech는 limited data에서 speaking style을 학습하기 어렵기 때문에 새로운 speaker에 대한 합성 품질이 떨어짐
• PVAE-TTS
  • Style에 점진적으로 adapting 하면서 data를 생성하는 Progressive Variational AutoEncoder를 채택
  • 추가적으로 adaptiation 성능을 향상하기 위해 Dynamic Style Layer Normalization을 도입
• 논문 (ICASSP 2022) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS) system을 training 하기 위해서는 고품질의 audio가 필요하므로 time-consuming 하고 laborous 함
  • 따라서 small training data로 고품질의 음성을 합성할 수 있는 adaptive TTS가 요구됨
    1. 이를 위해 새로운 speaker의 audio에서 추출된 speaker embedding에 따라 음성을 condition 하는 zero-shot adaptation을 사용할 수 있음
       - 대표적으로 Meta-StyleSpeech는 mel-encoder의 speaker embedding과 episodic meta-learning을 활용
    2. 한편으로 pre-trained TTS model을 fine-tuning 하는 adaptation 방식을 활용할 수도 있음
       - 대표적으로 AdaSpeech는 acoustic condition modeling과 Conditional Layer Normalization (CLN)을 도입
  • BUT, 여전히 adaptive TTS로 합성된 audio는 naturalness와 similarity가 부족하다는 한계가 있음
    - 이는 tone, stress 등의 extensive speaking style information을 few sample 만으로는 학습하지 못하기 때문

-> 그래서 limited data에서도 다양한 style adaptation을 지원할 수 있는 PVAE-TTS를 제안

 

• PVAE-TTS
  • Progressive Variational AutoEncoder (PVAE)를 도입하여 점진적으로 style-normalized representation을 추출하고 style adaptation을 수행
    - 이를 통해 limited data에서도 다양한 speaking style을 점진적으로 학습하여 고품질 생성이 가능
  • Adaptation 품질을 향상하기 위해 Dynamic Style Layer Normalization (DSLN)을 추가
    - Convolution operation을 통해 model이 style에 효과적으로 adapt 하도록 지원함

< Overall of PVAE-TTS >

• PVAE와 DSLN을 활용한 adaptive TTS model
• 결과적으로 기존보다 뛰어난 합성 품질을 달성

2. Progressive Variational AutoEncoder

• Style에는 다양한 factor가 포함되어 있기 때문에 적은 data로 style adaptation을 수행하는 것은 어려움
  • 따라서 논문은 bidirectional-inference variational autoencoder에 기반한 PVAE를 도입함 
  • 여기서 prior는 $p_{\theta}(\mathbf{x},\mathbf{z})=p_{\theta}(\mathbf{x}|\mathbf{z}_{1})\left[ \prod_{l=1}^{L-1} p_{\theta}(\mathbf{z}_{l}|\mathbf{z}_{l+1})\right]p_{\theta}(\mathbf{z}_{L})$로, 근사 posterior는 $q_{\phi}(\mathbf{z}|\mathbf{x})=q_{\phi}(\mathbf{z}_{1}|\mathbf{x})\left[ \prod_{l=1}^{L-1}q_{\phi}(\mathbf{z}_{l+1}|\mathbf{z}_{l})\right]$로 정의된다고 하자
    - $\mathbf{z} =\mathbf{z}_{1},...,\mathbf{z}_{L}$ : latent variable의 hierarchy, $L$ : hierarchy 수
  • 그러면 PVAE는 deterministic bottom-up path와 top-down path로 구성되고 서로 parameter를 sharing 함
    1. Bottom-up path를 따라 PVAE는 data $\mathbf{x}$에서 progressively style-normalized feature를 추출하고 
    2. Top-down path를 따라 stored style-normalized feature를 사용하여 style-adapted feature를 생성하고, evidence lower bound를 최대화함:
       (Eq. 1) $\mathcal{L}(\theta,\phi)\equiv \mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x})} [\log p_{\theta}(\mathbf{x}|\mathbf{z})]-D_{KL}(q_{\phi}(\mathbf{z}_{1}|\mathbf{x})|| p(\mathbf{z}_{1}))$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,- \sum_{l=2}^{L}\mathbb{E}_{q_{\phi}(\mathbf{z}_{<l}|\mathbf{x})}[ D_{KL}(q_{\phi}(\mathbf{z}_{l}|\mathbf{x},\mathbf{z}_{<l})|| p_{\theta}(\mathbf{z}_{l}|\mathbf{z}_{<l}) )]$
  • 추가적으로 PVAE는 bottom-up path를 따라 $P(\hat{s}=s_{i}|\mathbf{z}_{1,i})\geq ... \geq P(\hat{s}=s_{i}|\mathbf{z}_{L,i})$와 같이 점진적으로 speaker information을 remove 함
    - $\hat{s}$ : predicted style
    - $\mathbf{z}_{l}$ : style $s_{i}\in S$를 가지는 data $\mathbf{x}$로부터 얻어지는 progressively style-normalized representation ($S$ : style set)

3. PVAE-TTS

• 앞선 PVAE를 확장하여 PVAE-TTS는 phoneme encoder, mel-encoder, variance adaptor, 4 stack의 PVAE block으로 구성됨 
  • 각 PVAE block은 FastSpeech2의 FFT block을 기반으로 Progressive Top-Down (PTD) block과 Progressive Bottom-Up (PBU) block을 가짐
    - Phoneme encoder, variance adaptor 역시 FastSpeech2 architecture를 따름
  • 한편으로 multi-speaker TTS로 확장하기 위해 Meta-StyleSpeech와 같이 mel-encoder를 사용해 style embedding $e$를 추출함
    - 이후 style embedding $e$를 phoneme-level에서 duration/pitch/energy를 예측하는 각 variance adaptor의 input에 concatenate 함

Overall of PVAE-TTS

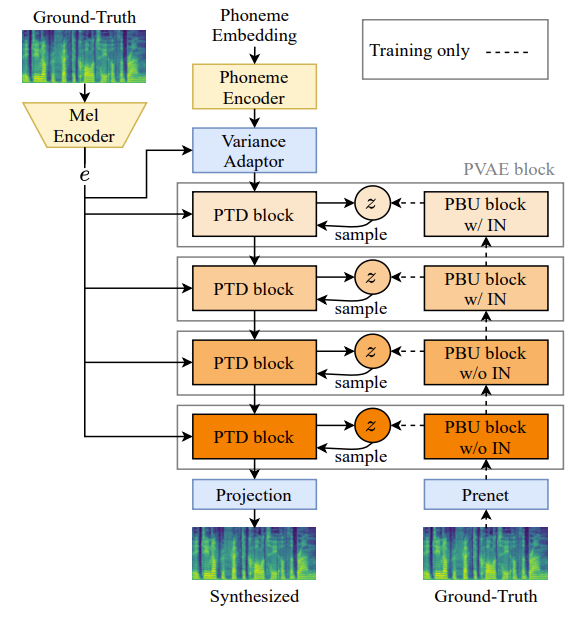
- Progressive Style Normalization

• Bottom-up path는 style information을 progressively remove 하여 hierarchical feature를 추출하는 것을 목표로 함 
  • 이때 style information을 remove 하기 위해 3, 4번째 PBU block에 Instance Normalization (IN)을 적용하고, 동일한 PBU block에 information bottleneck layer를 추가함 
  • 이를 통해 각 PBU block은 progressively style-normalized representation을 생성할 수 있음

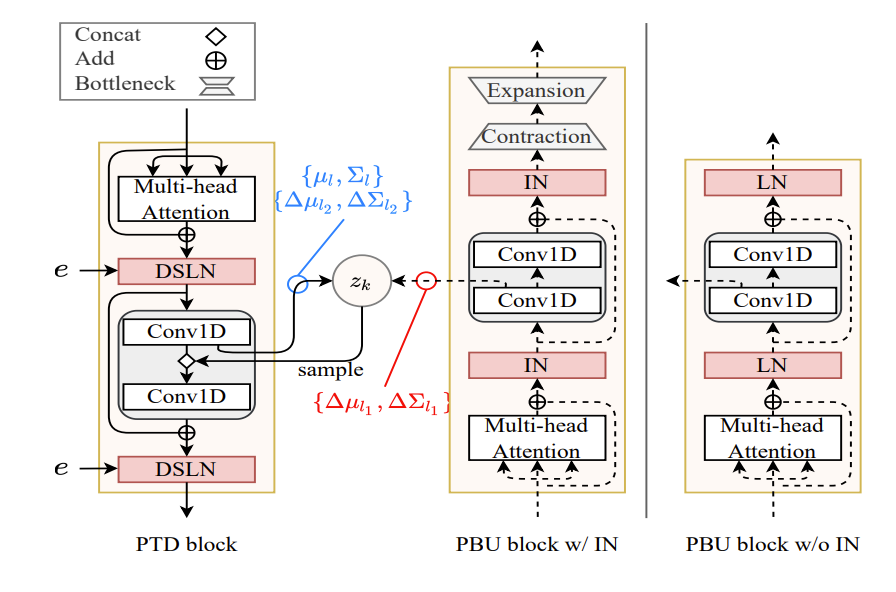
- Information Sharing

• 각 PBU, PTD block에서 prior와 근사 posterior distribution의 parameter $\{\mu_{l},\Sigma_{l}\},\{\Delta \mu_{l_{1}},\Delta \Sigma_{l_{1}}\}, \{\Delta\mu_{l_{2}},\Delta \Sigma_{l_{2}}\}$는 각 block의 preceding 1D convolution으로 얻어짐
  • 그러면 prior distribution $p_{\theta}(\mathbf{z}_{l}|\mathbf{z}_{<l},\mathbf{y})$와 근사 posterior distribution $q_{\phi}(\mathbf{z}_{l}|\mathbf{z}_{<l},\mathbf{x},\mathbf{y})$는:
    (Eq. 2) $p_{\theta}(\mathbf{z}_{l}|\mathbf{z}_{<l},\mathbf{y}):=\mathcal{N}(\mu_{l},\Sigma_{l})$
    (Eq. 3) $q_{\phi}(\mathbf{z}_{l}|\mathbf{z}_{<l},\mathbf{x},\mathbf{y}):=\mathcal{N}(\mu_{l}+\Delta \mu_{l_{1}}+\Delta\mu_{l_{2}}, \Sigma_{l}\cdot \Delta\Sigma_{l_{1}}\cdot \Delta \Sigma_{l_{2}})$
    - $\Sigma$ : covariance matrix, $\mathbf{x}$ : mel-spectrogram, $\mathbf{y}$ : text
    - 이때 분산은 음수가 될 수 없으므로, $\Sigma$에 softplus function을 적용함
  • 근사 posterior distribution은 top-down prior information으로부터 bottom-up path와 generative distribution의 근사 likelihood를 포함하는 overall information으로 볼 수 있음
  • Training 중에 latent variable $\mathbf{z}_{l}$은 근사 posterior $q_{\phi}(\mathbf{z}_{l}|\mathbf{z}_{<l},\mathbf{x},\mathbf{y})$에서 sampling되고, 추론 시에는 prior $p_{\theta}(\mathbf{z}_{l}|\mathbf{z}_{<l}, \mathbf{y})$에서 sampling 됨 
  • 해당 architecture를 통해 bottom-up path는 style-normalized information을 top-down path와 share 하므로, progressive style adaptation을 지원할 수 있음 

- Progressive Style Adaptation

• Top-down path를 따라 text information은 progressive style adaptation을 통해 mel-spectrogram으로 변환됨
  • 이때 각 PTD block은 PBU block이 share 하는 progressively style-normalized feature를 사용하여 style-adapted feature를 생성함
  • 한편으로 AdaSpeech의 CLN과 Meta-StyleSpeech의 SALN은 element-wise product나 matrix addition을 사용하여 encoder output에 style embedding $e$를 반영함
    - BUT, 해당 simple operation으로는 다양한 style information을 효과적으로 반영하기 어려움
  • 따라서 PVAE-TTS에서는 DSLN을 통해 style embedding $e$로 condition 되는 hidden vector $h$를 input으로 사용함
    1. 먼저 filter weight $\mathbf{W}_{e}$를 예측하기 위해 single linear layer를 추가하고 $e$에서 bias $\mathbf{b}_{e}$를 얻음 
    2. 이후 DSLN은 1D group-convolution을 수행하여 style-adapted feature를 생성함:
       (Eq. 4) $\text{DSLN}(h,e)=\mathbf{W}_{e}\odot \text{LN}(h)+\mathbf{b}_{e}$
       - $\odot$ : nomalized $h$와 주어진 weight $\mathbf{W}_{e}$, bias $\mathbf{b}_{e}$에 대한 convolution operation
       - $\{\mathbf{W}_{e}, \mathbf{b}_{e}\}$는 learnable parameter가 아니라 주어진 style $e$에 따라 adaptively predict 됨
  • 결과적으로 아래 그림과 같이 모든 PTD block에 DSLN이 추가되고, 해당 DSLN을 통해 PVAE-TTS는 high-adaptation을 지원할 수 있음 

PTD, PBU Block

- Training Objectives

• PVAE-TTS는 variational inference를 수행함
  • 이때 text information을 사용하여 top-down path를 따라 mel-spectrogram을 생성:
    (Eq. 5) $\mathcal{L}_{recon}=-\mathbb{E}_{q_{\phi}(\mathbf{z}|\mathbf{x},\mathbf{y})}[\log p_{\theta}(\mathbf{x}|\mathbf{z},\mathbf{y})]$
    (Eq. 6) $\mathcal{L}_{KL}=D_{KL}(q_{\phi}(\mathbf{z}_{1}|\mathbf{x},\mathbf{y})|| p(\mathbf{z}_{1}|\mathbf{y}))+\sum_{l=2}^{L}\mathbb{E}_{q_{\phi}(\mathbf{z}_{<l}|\mathbf{x},\mathbf{y})}[D_{KL} (q_{\phi}(\mathbf{z}_{l}|\mathbf{x},\mathbf{y},\mathbf{z}_{<l})|| p_{\theta}(\mathbf{z}_{l}|\mathbf{y},\mathbf{z}_{<l}))]$
  • PVAE-TTS의 overall loss function은:
    (Eq. 7) $\mathcal{L}_{total}=\mathcal{L}_{recon}+\beta \mathcal{L}_{KL}+\lambda \mathcal{L}_{var}$
    - $\beta$ : 첫 20% training step 동안 $0$에서 $1$로 증가하는 값, $\lambda = 1$
    - $\mathcal{L}_{var}$ : variance predictor의 $L_{2}$ distance의 합
    

4. Experiments

- Settings

• Dataset : LibriTTS, VCTK
• Comparisons : FastSpeech2, Meta-StyleSpeech

- Results

• 전체적으로 PVAE-TTS가 가장 우수한 성능을 달성함

모델 성능 비교

• Zero-shot $^{\lozenge}$, few-shot $^{\star}$ adaptation측면에서도 PVAE-TTS의 성능이 가장 뛰어남

Zero-/Few-shot Adaptation 성능

• PBU block의 효과를 알아보기 위해 PBU block에서 speaker ID를 classify 하는 classifier를 training 해보면
  • IN만 사용하거나 bottleneck만을 사용하면 speaker information이 조금만 제거됨
  • 반면 IN, information bottleneck을 모두 사용하는 경우, speaker information을 점진적으로 제거 가능

(a) Adaptation sample 수에 따른 MOS 비교 (b) PBU block의 효과

• Ablation study 측면에서 각 component를 제거하는 경우 성능 저하가 발생함

Ablation Study 결과