[Paper 리뷰] Singing Voice Synthesis Using Differentiable LPC and Glottal-Flow-Inspired Wavetables

Singing Voice Synthesis Using Differentiable LPC and Glottal-Flow-Inspired Wavetables

---

• Singing Voice Synthesis를 위해 human voice의 physical characteristic을 활용할 수 있음
• Glottal-Flow LPC Filter (GOLF)
  • Harmonic source로써 glottal model을 사용하고, vocal tract를 simulate 하기 위해 IIR filter를 활용
    
  • GOLF는 더 적은 parameter와 memory를 사용함으로써 빠른 추론이 가능함
  • GOLF는 singing voice를 다양화할 수 있는 phase component를 modelling할 수 있음
• 논문 (ISMIR 2023) : Paper Link

---

1. Introduction

• Singing Voice Synthesis (SVS)는 musical context factor (note, duration, phoneme 등)을 고려하여 acoustic model과 vocoder를 통해 수행됨
  • 초기에는 linear source-filter 모델을 주로 활용했고 이후 Deep Neural Network (DNN)의 등장으로 vocoder가 크게 개선됨
  • BUT, 이러한 vocoder는 주로 mel-spectrogram을 input으로 사용하는데 f0, aperiodicity ratio와 같은 vocoder parameter에 비해 interpretable 하지 않음
    
• Differentiable Digital Signal Processing (DDSP)는 기존의 signal processing을 inductive bias로 neural network에 통합하여 interpretability를 향상함
  • 특히 SVS 작업에서 DDSP 활용은 다양함
    - Substractive synthesis와 sawtooth를 harmonic source로 활용하는 방법
    - Taylor expansion을 통해 mel-log spectrum approximation filter (MLSA)의 exponential function을 근사하는 방법
  • BUT, 위의 방법들은 target signal이 monophonic instrument라고 가정하므로 voice property를 제대로 반영하지 못함
    -> 따라서 harmonic source와 filter에 human voice에 대한 특정 제약을 반영하면 더 interpretable하고 compact 한 SVS vocoder를 구성할 수 있음

-> 그래서 human voice의 physical property를 활용하는 SVS module인 Glottal-Flow LPC Filter (GOLF)를 제안

 

• Glottal-Flow LPC Filter (GOLF)
  • DDSP의 harmonic-plus-noise architecture와 SawSing의 substractive synthesis를 기반으로 활용
  • 이때 harmonic source를 glottal model로 대체하고, IIR filter를 적용
    - 효율적인 학습을 위해 IIR filter는 differentiable 하도록 구현됨
  • 결과적으로 human voice의 phase component를 반영하고 더 compact한 architecture를 구성 가능

< Overall of GOLF >

• GOLF는 훨씬 적은 수의 parameter로도 다른 SVS vocoder에 대해 경쟁력 있는 결과를 달성함
• GOLF는 학습을 위해 40% 미만의 memory만을 요구하고 추론은 다른 모델들에 비해 10배 빠르게 실행됨

2. Background

• Notations
  • $\mathbf{x}_{i}$ : $i$-th column vector, $x_{i,j}$ : matrix $\mathbf{X}$의 $i$-th row, $j$-th column의 성분
  • $[;]$ : column dimension에 대한 두 matrix 간의 concatenation
  • $x_{i}$ : vector $\mathbf{x}$의 $i$-th 성분 / $i$로 index 된 time sequence 
  • $X(z)$ : $z$-domain에서 $x_{n}$의 response 
  • $n$ : time index, $k$ : frame index
    
  • Angular frequency와 period는 $[0,1]$의 범위로 normalize됨

- Glottal Source-Filter Model

• Source-filter model에서 아래의 단순한 voice production model을 생각할 수 있음:
  (Eq. 1) $S(z) = (G(z) + N(z)) H(z) L(z)$
  - $G(z)$ : vocal folds의 periodic vibration
  - $N(z)$ : glottal source의 random component
  - $H(z)$ : vocal-tract filter
  - $L(z)$ : lip에서의 radiation
• (Eq. 1)은 linear 하기 때문에 radiation filter $L(z)$와 glottal pulse $G(z)$는 radiated glottal pulse $G'(z)$로 merge 될 수 있음
  • $L(z)$가 first-order differentiator $1+z^{-1}$라고 가정하면, $G'(z)$는 glottal pulse의 deriative
    - 이는 glottal flow에 대한 four-parameter model인 LF model로써 표현 가능
  • $H(z)$는 일반적으로 Linear Predictive Coding (LPC) filter를 사용함

- Linear Predictive Coding

• LPC는 현재 음성 sample $s_{n}$이 residual error $e_{n}$과의 linear combination을 통해 $M$개의 이전 sample $s_{n-1}$부터 $s_{n-M}$까지로부터 예측될 수 있음:
  (Eq. 2) $s_{n} = e_{n} - \sum_{i=1}^{M} a_{i}s_{n-i}$
  - $a_{i}$ : linear prediction coefficient
• 이는 Infinite Impulse Response (IIR)을 갖는 $M$-th order all-pole filter를 사용하여 glottal source를 filtering 하는 것과 동일함
  
  • Vocal tract가 다양한 diameter를 가지는 cylinderical tube로 근사되는 경우, LPC filter를 사용하여 vocal tract response를 표현할 수 있고 physical interpretation도 제공함
  • 이때 (Eq. 2)를 사용하여 IIR을 학습하는 것은 계산이 recursive 하기 때문에 어려울 수 있음
    - 이로 인해 상당한 memory allocation 및 overhead가 발생하고 특히 긴 sequence의 경우 성능 저하로 이어짐
    -> 따라서 이를 완화하기 위한 적절한 방법이 필요함

3. Proposed Model

• 일반적으로 (Eq. 1)의 $N(z)$는 amplitude-modulated Gaussian noise로 처리되지만 최적화하기 어려움
  • 이를 대체하기 위해 noise component $N(z)$를 glottal source의 outside로 이동하고, time-varying filter $C(z)$를 적용:
    (Eq. 3) $S(z) = G'(z)H(z) + N(z)C(z)$
  • 이는 DDSP에서 사용된 Harmonic-plus-Noise model과 유사한 형태
    - GOLF는 glottal-flow model을 사용하여 harmonic source와 time-varying IIR filter를 합성
    

- Glottal Flow Wavetables

• Glottal pulse를 생성하기 위해 transformed-LF model을 채택
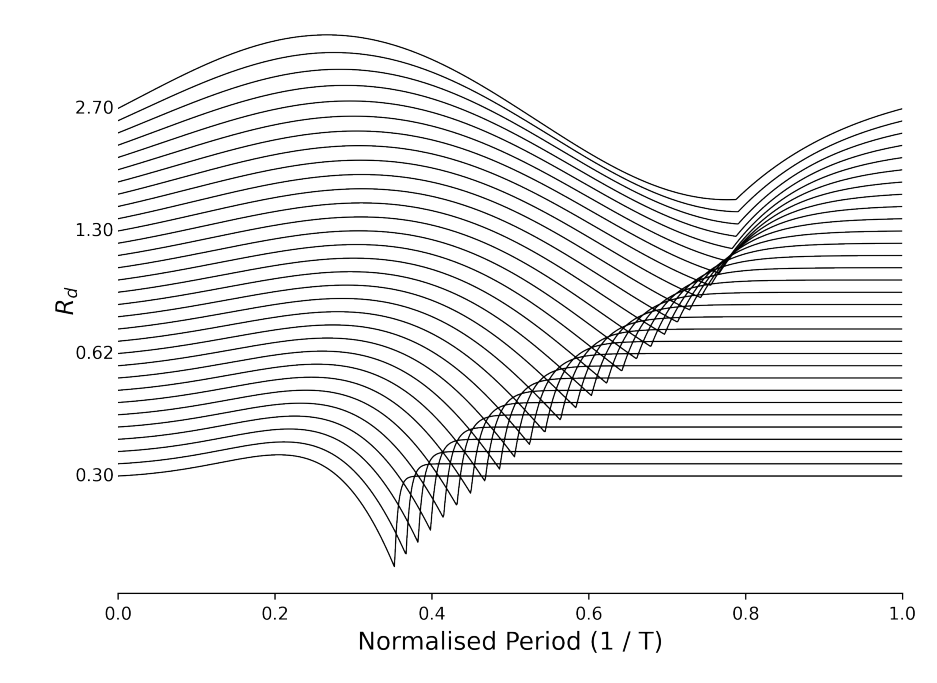
  • 다양한 glottal flow shape를 나타낼 수 있는 하나의 parameter $R_{d}$를 사용하여 LF model을 reparameterize 함
    1. $[log(0.3), log(2.7)]$ 범위에서 동일한 간격으로 $K$개의 $log(R_{d})$ 값을 sampling
    2. Sampling 된 각 $R_{d}$에 대해 continuous time $t$에서 flow derivative function $g'(t;R_{d})$를 계산
    3. 이후 하나의 period에 대해 $L$ point를 sampling 하여 discrete version을 얻음
  • 위와 같이 sampling 된 glottal flow를 stack하여, 각 row에 sampling된 glottal pulse의 하나의 period를 포함하는 wavetable $\mathbf{D} \in \mathbb{R}^{K \times L}$을 구축
    - 이때 row는 $R_{d}$를 기준으로 sort
• Model은 2개의 $\mathbf{D}$ axis를 linear interpolating 하여 glottal pulse $g_{n}^{'}$을 생성
  • Encoder network는 $R_{d}$에 대한 instantaneous frequency $f_{n} \in [0, 0.5]$와 fractional index $\tau_{n} \in [0,1]$을 예측
  • 이후 instantaneous phase $\phi_{n} = \sum_{i=1}^{n} f_{i}$를 사용하여 waveform을 interpolate:
    (Eq. 4) $g^{'}_{n} = (1-p)\left( (1-q)\hat{d}_{\lfloor k \rfloor, \lfloor l \rfloor} + q\hat{d}_{\lfloor k \rfloor, \lceil l \rceil}\right) + p \left( (1-q)\hat{d}_{\lceil k \rceil, \lfloor l \rfloor} + q\hat{d}_{\lceil k \rceil, \lceil l \rceil} \right)$
    - $l = (\phi_{n}, mod \, \, 1)L + 1$, $k= \tau_{n} (K-1)+1$, $p= k-\lfloor k \rfloor$, $q=l-\lfloor l \rfloor$
    - $\hat{\mathbf{D}} = [\mathbf{D}; \mathbf{d}_{1}] \in \mathbb{R}^{K \times (L+1)}$
    - Wavetable $\mathbf{D}$는 fix 되어 있고, weighted sum을 사용하지 않고 한 번에 하나의 wavetable만 사용

Wavetable

- Frame-wise LPC Synthesis

• Time-varying LPC synthesis는 LPC coefficient를 audio resolution에 linearly interpolating 하고 sample 별로 filtering 하여 수행됨
  
  • 이러한 방식은 병렬화가 불가능하므로 학습 속도를 느리게 만듦
  • 따라서 GOLF는 각 frame을 독립적으로 처리하고 overlap-add를 사용하여 LPC synthesis를 근사:
    (Eq. 5) $s_{n} = \sum_{k} LPC(g_{n}^{'}\gamma_{n}u_{n-kT};\mathbf{a}_{k})w_{n-kT}$
    - $LPC(e_{n}, \mathbf{a})$ : (Eq. 2), $\mathbf{a}_{k} \in \mathbb{R}^{M}$ : $k$-th frame의 filter coefficient
    - $u_{n}, w_{n}$ : windowing function, $\gamma_{n} \in \mathbb{R}^{+}$ : gain, $T$ : hop size
  • 위를 통해 LPC synthesis를 병렬적으로 계산할 수 있음
    - 특히 충분히 작은 hop size를 사용하면 overlap-add LPC와 sample별 LPC 간의 음성 품질 차이가 거의 나타나지 않음
    - 경험적으로 200Hz의 frame rate로도 충분함

- LPC Coefficients Parameterization

• LPC filter가 stable 하기 위해서는 모든 pole들이 complex plane의 unit circle 내에 존재해야 함
  • 이때 stability는 reflection coefficient와 같은 robust representation을 통해 보장될 수 있음
    
  • GOLF에서는 cascaded 2nd-order IIR filter를 representation으로 활용하여 모든 2nd-order filter가 stable 함을 보장
  • 이때 coefficient representation을 사용하여 encoder output에서 $i$-th IIR filter의 coefficient $1+\eta_{i,1}z^{-1} + \eta_{i,2}z^{-2}$를 parameterize
    - 이후 이를 cascade 하여 $M$-th order LPC filter를 구성:
    (Eq. 6) $(1+\eta_{1,1}z^{-1}+\eta_{1,2}z^{-2})(1+\eta_{2,1}z^{-1}+\eta_{2,2}z^{-2}) ... (1+\eta_{\frac{M}{2},1}z^{-1}+\eta_{\frac{M}{2},2}z^{-2})$
    $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,= 1 + a_{1}z^{-1}+a_{2}z^{-2}+ ... + a_{M}z^{-M} = A(z)$

- Unvoiced Gating

• Encoder에 의해 예측된 instantaneous frequency $f_{n}$은 non-zero이고 oscillator가 동작하도록 함
  • 이때 적절한 제약이 없으면, 모델은 unvoiced region에서 buzzing artifact를 생성하게 됨
  • 따라서, $v_{n} \in [0,1]$로 voiced/unvoiced 확률을 예측하도록 모델을 jointly training 함
    - 이때 gated frequency $\hat{f}_{n} = v_{n}f_{n}$을 oscillator에 입력하여 artifact 생성 문제를 완화

4. Optimization

• DNN은 전체 computational graph에서 loss function $\mathcal{L}$로 evaluate 된 gradient를 parameter에 backpropagation 하여 학습됨
  • IIR Filter를 differentiable 하게 유지하면서 계산 복잡도를 줄이기 위해 time에 따른 closed form backpropagation을 유도
    - $\mathbf{e} \in \mathbb{R}^{N}$ : input
    - $\mathbf{a} \in \mathbb{R}^{M}$ : filter coefficient
    - $\mathbf{s} \in \mathbb{R}^{N}$ : output
    
  • $\frac{\partial \mathcal{L}} {\partial \mathbf{s}}$를 안다고 가정했을 때, chain rule $\frac{\partial \mathcal{L}} {\partial \mathbf{s}} \frac{\partial \mathbf{s}} {\partial \mathbf{e}}$과 $\frac{\partial \mathcal{L}} {\partial \mathbf{s}} \frac{\partial \mathbf{s}} {\partial \mathbf{a}}$를 통해 $\frac{\partial \mathcal{L}} {\partial \mathbf{e}}$와 $\frac{\partial \mathcal{L}} {\partial \mathbf{a}}$를 얻을 수 있음

- Backpropagation Through the Coefficients

• $a_{i}$에 대해 (Eq. 2)의 derivative를 취하면:
  (Eq. 7) $\frac{\partial s_{n}} {\partial a_{i}} = -s_{n-i} - \sum_{k=1}^{M} a_{k}\frac{\partial s_{n-k}} {\partial a_{i}}$
  - 위 식은 $LPC(-s_{n-i} ; \mathbf{a})$와 동일하고, $s_{n}|_{n \leq 0}$은 $a_{i}$에 의존하지 않으므로 initial condition $\frac{\partial s_{n}} {\partial a_{i}}|_{n\leq 0} = 0$
  - 이때 $\frac{\partial s_{n}} {\partial a_{j}}$가 offset $j-i$만큼 shift된 $\frac{\partial s_{n}} {\partial a_{i}}$이기 때문에 한번의 filtering으로 $\frac{\partial s_{n}} {\partial \mathbf{a}}$를 얻을 수 있음
  - $\frac{\partial \mathcal{L}} {\partial a_{i}}$는 $\sum_{n=1}^{N} \frac{\partial \mathcal{L}}{\partial s_{n}} \frac{\partial s_{n}} {\partial a_{i}}$로 계산할 수 있음

- Backpropagation Through the Input

• Input $e_{n}$에 대한 derivative를 얻기 위해 (Eq. 2)를 convolution form으로 다시 쓰면:
  (Eq. 8) $s_{n}= \sum_{m=1}^{n}e_{m}h_{n-m}$
  - $h_{n} = \mathcal{Z}^{-1} \{ H(z) \}$, $H(z) = \frac{1}{A(z)}$
  
• (Eq. 8)로부터 $\frac{\partial s_{n}} {\partial e_{m}} = h_{n-m}$이고, 이때 $e_{m}$에 대한 loss $\mathcal{L}$의 derivative는 모든 future sample $s_{n}$에 따라 달라짐:
  (Eq. 9) $\frac{\partial \mathcal{L}}{\partial e_{m}} = \sum_{n=m}^{N}\frac{\partial \mathcal{L}}{\partial s_{n}} \frac{\partial s_{n}}{\partial e_{m}} = \sum_{n=m}^{N}\frac{\partial \mathcal{L}}{\partial s_{n}}h_{n-m}$
• 이때 $n, m$을 swapping 하고 (Eq. 2)와 (Eq. 8)의 equivalance를 고려하면 (Eq. 9)를 단순화할 수 있음:
  (Eq. 10) $\frac{\partial \mathcal{L}}{\partial e_{n}} = \sum_{m=n}^{N}\frac{\partial \mathcal{L}}{\partial s_{m}}h_{m-n} = \frac{\partial \mathcal{L}}{\partial s_{n}} - \sum_{i=1}^{M}a_{i}\frac{\partial \mathcal{L}}{\partial e_{n+i}}$
  - (Eq. 10)은 동일한 filter로 $\frac{\partial \mathcal{L}} {\partial s_{n}}$을 filtering하고 $\frac{\partial \mathcal{L}} {\partial e_{n}}$에 대한 derivative를 얻을 수 있다는 것을 의미함
  - 이때 initial condition $\frac{\partial \mathcal{L}} {\partial e_{n}} |_{n > N} = 0$
  - 결과적으로 IIR filter를 통한 backpropagation은 동일한 filter에 대한 2번의 pass와 1번의 matrix multiplication으로 구성됨
  

Overall of GOLF

5. Experiments

- Settings

• Dataset : MPop600
• Comparisons : DDSP, SawSing, PULF

- Results

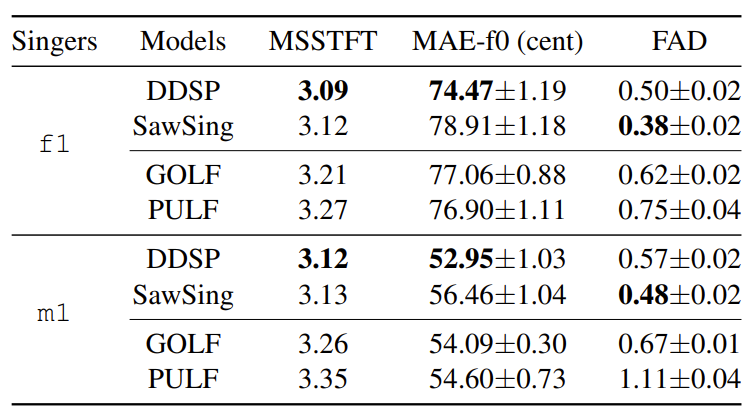
• Objective Evaluation
  • GOLF는 MSSTFT, MAE-f0, FAD 측면에서 다른 모델들과 비슷한 수준의 합성 품질을 보임
  • Memory 사용량 및 RTF 측면에서는 GOLF가 가장 효율적인 것으로 나타남
    - 특히 CPU에서 GOLF는 다른 모델에 비해 35% 적은 memory 만을 사용
  • 결과적으로 GOLF의 합성 품질은 다른 모델에 비해 특별히 뛰어나지는 않지만, memory 사용량 및 RTF 측면에서 상당히 우수함

합성 품질 비교

• 예측된 waveform과 ground-truth waveform 사이의 L2 loss를 비교
  • GOLF와 PULF는 IIR filtering을 통해 non-linear phase response를 도입할 수 있음
  • 결과적으로 GOLF의 L2 loss가 가장 낮기 때문에 phase reconstruction 능력이 가장 뛰어나다고 할 수 있음

Memory 사용량, RTF 비교

• Subjective Evaluation
  • MOS 측면에서 주관적인 합성 품질 평가를 수행
  • DDSP가 가장 우수한 품질을 보이는 것으로 나타났으나 GOLF와 통계적인 측면에서 유의함을 보이지는 않음
  • GOLF는 PULF, SawSing과 비교했을 때, Wilcoxon signed-rank test에서 통계적으로 유의한 성능 차이를 보임

MOS 비교

• Discussion
  • Ground-truth waveform과 각 모델들의 waveform을 비교했을 때, GOLF가 가장 비슷한 waveform을 생성함
  • 이러한 결과는 waveform에 대한 L2 loss를 줄임으로써 phase reconstruction을 개선하는 효과로 이어짐

예측된 waveform 비교