[Paper 리뷰] LightGrad: Lightweight Diffusion Probabilistic Model for Text-to-Speech

LightGrad: Lightweight Diffusion Probabilistic Model for Text-to-Speech

---

• Text-to-Speech 모델은 효율적인 일상 활용을 위해 edge device에 배포하는 것이 요구됨
• Diffusion probabilistic model 은 다른 생성 모델들에 비해 안정적으로 학습되고  parameter 효율성이 높음
• LightGrad
  • Edge device에서 TTS를 활용하기 위한 경량 diffusion probabilistic model 
  • 경량 U-Net diffusion decoder와 빠른 sampling, streaming inference를 통한 latency 감소
• 논문 (ICASSP 2023) : Paper Link

---

1. Introduction

• 일상생활에서 Text-to-Speech (TTS) 수요 증가로 인해 여러 neural TTS 모델들이 클라우드 환경에 배포되어 서비스되고 있음
  
  • BUT, 클라우드 환경은 개인 정보 보호 및 latency 제약 등으로 인해 한계가 있음
    - 클라우드 통신과정에서 data 및 사용자 정보가 노출될 위험성
    - 클라우드 통신으로 인한 네트워크 민감성 및 user perceived latency 증가
  • Edge device에서 활용할 수 있는 경량화된 neural TTS 모델이 요구됨
• 단순 분포를 복잡한 분포로 점진적으로 변환할 수 있는 Markov chain 기반의 Diffusion Probabilistic Model (DPM)이 등장
  • GAN, Flow-based model과 비교했을 때, DPM은 더 안정적으로 최적화되고 parameter 효율성이 높음
    - 특히 Grad-TTS는 TTS 작업에서 합성 품질을 향상하고 추론 과정의 계산량을 크게 줄일 수 있음을 보임
  • BUT, edge device에 대한 경량 TTS DPM에 대한 연구는 부족함
    - TTS용 DPM 설계의 어려움 때문
    1. 현재의 TTS용 DPM은 edge device에 배포할 만큼 가볍지 않음
    2. DPM은 추론 과정에서 많은 denoising 단계가 필요하므로 추론시간이 길어질 수 있음
  • Edge device에서 DPM을 활용하기 위해서는, parameter와 추론 latency를 모두 줄일 수 있어야 함

-> 그래서 edge device에 적합한 경량 TTS DPM인 LightGrad를 제안

 

• LightGrad
  • 작은 모델 크기와 빠른 추론 속도를 가지는 TTS용 경량 DPM
  • Diffusion decoder의 regular convolution을 depthwise separable convolution으로 대체
  • 추론 속도 향상을 위해 training-free sampling 기법을 도입

< Overall of LightGrad >

• Encoder, duration predictor, 경량 U-Net decoder로 구성된 non-autoregressive TTS 모델
  - U-Net decoder는 추정된 prior 분포에서 sampling 된 noise를 점진적으로 변환하여 mel-spectorgram을 생성
• U-Net decoder의 경량화를 위해 depthwise separable convolution을 도입
• Sampling 속도 향상을 위한 DPM-solver의 활용 및 추론 latency를 줄이기 위한 streaming inference 도입

2. Methodology

- Background on Diffusion Probabilistic Model

• DPM의 basic idea:
  1. Forward process는 white noise를 점진적으로 추가하여 data 분포를 isotropic Gaussian noise로 변환
  2. Backward process는 학습된 network가 Gaussian noise로부터 data를 반복적으로 복원
• Forward Process
  • LightGrad의 forward process는:
    (eq.1) $dX_{t} = \frac{1}{2} (\mu - X_{t}) \beta_{t} dt + \sqrt{\beta_{t}} d W_{t}, \, t \in [0,T]$
    - $\mu$ : Gaussian prior $\mathcal{N}(\mu, I)$의 mean, $\beta_{t}$ : noise schedule, $W_{t}$ : Brownian motion
  • Forward process는 stochastic process $\{ X_{t} \} ^{T}_{t=0}$을 생성함
    - $X_{t} \sim p(X_{t})$라고 가정하면, forward process는 data 분포 $p(X_{0})$를 $p(X_{T}) \sim \mathcal{N}(\mu, I)$로 변환
  • 주어진 $X_{0}$에 대해:
    (eq.2) $p(X_{t} | X_{0}) = \mathcal{N} (\mu_{t}, \Sigma_{t})$
    - 위를 통해 $X_{t}$를 효율적으로 sampling할 수 있음 
    - (eq.3) $\mu_{t} = (I - e^{\frac{1}{2} \rho_{t}}) \mu + e^{\frac{1}{2} \rho_{t}} X_{0}$, $\Sigma_{t} = I - e^{\rho_{t}}$, $\rho_{t} = - \int_{0}^{t} \beta_{s} ds$
• Backward Process
  • $X_{T}$로부터 $X_{0}$을 복원하기 위해서, $X_{T}$에서 backward Stochastic Differential Equation (SDE)를 계산함
  • Backward SDE는:
    (eq.4) $dX_{t} = (\frac{1}{2} (\mu-X_{t}) - \nabla log p_{t}) \beta_{t} dt + \sqrt{\beta_{t}} d \widetilde{W}_{t}$
    - $\widetilde{W}_{t}$ : reverse-time Brownian motion, $\nabla log p_{t}$: $p(X_{t})$의 score
  • 이때, 위 식은 Ordinary Differential Equation (ODE)과 동일한 marginal probability density를 공유함:
    (eq.5) $dX_{t} = \frac{1}{2} ( (\mu-X_{t}) - \nabla log p_{t}) \beta_{t} dt$
  • 따라서, $t \in [0,T]$에 대해 $\nabla log p_{t}$를 추정하도록 학습된 network가 있는 경우, $p(X_{T})$에서 $X_{T}$를 sampling하고 위의 backward equation (eq.4) 또는 (eq.5)를 따라 $X_{0}$로 변환할 수 있음
• Training LightGrad
  • DPM으로 sample을 생성하기 위해, neural network $s_{\theta}$는 $X_{t}, t, \mu$가 주어졌을 때 $\nabla log p_{t}$를 추정하도록 학습됨
    - $X_{0}$에 condition이 적용된 경우, (eq.2)를 사용하여 $X_{t}$를 직접 sampling할 수 있음
  • 이때, $p(X_{t} | X_{0})$의 score는:
    (eq.6) $\nabla log p(X_{t} | X_{0}) = - \frac{\epsilon_{t}} {\sqrt{\Sigma_{t}}}, \, \epsilon_{t} \sim \mathcal{N} (0, I) $
  • 따라서 $s_{\theta}$를 학습시키기 위한 diffusion loss function은:
    (eq.7) $L_{t} = \mathbb{E}_{X_{0, t}} [ \mathbb{E}_{\epsilon_{t}} || \sqrt{\Sigma_{t}} s_{\theta} (X_{t}, \mu, t) + \epsilon_{t} || ^{2} ]$
  • Diffusion loss 외에 추가적으로 Grad-TTS와 유사한 negative log-likelihood encoder loss가 encoder ouput에 적용됨
    - Duration predictor는 logarithmic duration을 추정하기 위해 mean squared error를 통해 학습됨
    - Encoder output과 Target mel-spectorgram 간의 alignment는 Monotonic Alignment Search (MAS)를 통해 추정됨

- Fast Sampling Technique

• DPM의 sampling 과정은 (eq.4), (eq.5)의 backward SDE나 ODE를 수치적으로 푸는 것과 동일
  • LightGrad는 DPM sampling을 위해 (eq.5)의 ODE를 활용
    - (eq.5)는 data variable에 대한 linear function과 non-linear network인 $s_{\theta}$로 구성된 semi-linear structure를 가짐
    - Semi-linear structure를 무시하는 일반적인 ODE-solver는 linear, non-linear term 모두에서 discretization error를 발생시킴
• 따라서 sampling 효율성 향상을 위해 (eq.5)에 맞는 DPM-solver를 채택함
  • $\nabla log p_{t}$를 추정하도록 학습된 neural network $s_{\theta}$가 있다고 가정하면,
    - Sampling process는 $X_{T} \sim \mathcal{N}(\mu, I)$에서 시작해 (eq.5)를 time에 따라 backward로 풀면 됨:
    (eq.8) $dX_{t} = \frac{1}{2} ( (\mu - X_{t}) - s_{\theta} (X_{t}, t, \mu) ) \beta_{t} dt$
    
  • 이때 $Y_{t} = X_{t} - \mu$, $Y_{T} \sim \mathcal{N} (0, I)$라고 하면:
    (eq.9) $dY_{t} = -\frac{1}{2} \beta_{t} Y_{t} dt - \frac{1}{2} \beta_{t} s_{\theta} (Y_{t} + \mu, \mu, t) dt$
    - 위 식은 $Y_{t}$에 대한 linear function인 $-\frac{1}{2} \beta_{t} Y_{t} dt$와 non-linear function인 $-\frac{1}{2} \beta_{t} s_{\theta} (Y_{t} + \mu, \mu, t)dt$로 구성된 semi-linear structure
    
  • $s \in (0,T)$, $t \in [0,s]$에 대해 (eq.9)에 대한 exact solution은:
    (eq.10) $Y_{t} = \frac{\alpha_{t}} {\alpha_{s}} Y_{s} + \alpha_{t} \int_{\lambda_{s}}^{\lambda_{t}} e^{-\lambda} \sqrt{\Sigma_{\tau_{\lambda}}} s_{\theta} (Y_{\tau_{\lambda}} + \mu, \mu, \tau_{\lambda}) d\lambda$
    - (eq.11) $\alpha_{t} = e^{\frac{1}{2} \rho_{t}}$, $\sigma_{t} = \sqrt{\Sigma_{t}}$, $\lambda_{t} = \lambda(t) = log \frac{\alpha_{t}}{\sigma_{t}}$, $\tau_{\lambda} = \lambda^{-1} (\lambda)$
• Time $s$에서의 $Y_{s}$가 주어지면, $Y_{t}$에 대한 근사해는 (eq.10)에 대한 근사 적분과 동일하므로 linear term의 error를 방지할 수 있음
  • Taylor expansion을 통해 $s_{\theta}$의 지수 가중 적분을 대체하고, $s_{\theta}$의 첫 번째 $(k-1)$차 도함수를 근사하면, $k$차 ODE-solver인 DPM-solver-$k$를 얻을 수 있음
    
  • LightGrad는 아래의 DPM-solver-1을 사용함:
    (eq.12) $Y_{t} = \frac{\alpha_{t}}{\alpha_{s}} Y_{s} + \sigma_{t} (e^{\lambda_{t}-\lambda_{s}} -1 ) \sqrt{\Sigma_{s}} s_{\theta} (Y_{s} + \mu, \mu, s)$

- Lightweight U-Net

• 경량 U-Net은 Grad-TTS diffusion decoder의 regular convolution을 depthwise separable convolution으로 대체한 것
  • 경량 U-Net은 3개의 downsampling block, 1개의 middle block, 2개의 upsampling block, 1개의 final convolution block으로 구성됨
    - Down/Up-sampling block은 separable resnet block (SepResBlock)과 linear attention layer (LA layer)로 구성
  • SepResBlock은 2개의 2D depthwise separable convolution (SepConv2d)와 group normalization, Mish activation을 가짐
    - Diffusion 단계는 sinusodial position embedding으로 표현됨
    - Step embedding을 얻기 위해 2개의 linear layer와 Mish activation을 사용
    - 각 SepResBlock에는 step embedding shape을 조절하기 위한 추가적인 linear layer가 적용됨
    - 첫 번째 Mish layer의 output에 step embedding을 더해 diffusion step information을 SepResBlock에 injection
  • LA layer는 input에 대한 linear self-attention을 수행
    1. Input은 3개의 SepConv2d에 전달되어 query, key, value를 가져옴
    2. Key는 softmax로 처리되고, value와 곱해져 context를 얻음
    3. 최종적인 attention output을 얻기 위해 context에 query를 곱함
  • Downsampling block은 2개의 SepResBlock, 1개의 LA layer, 1개의 downsampling convolution (DS Conv2d)로 구성
    - Middle block은 LA layer와 2개의 SepResBlock으로 구성
    - Upsampling block은 downsampling의 DS Conv2d를 transpose upsampling convolution (US TransConv2d)으로 대체
    - 마지막 upsampling layer에서 group normalization을 포함한 2개의 convolution을 통해 최종 output을 생성

LightGrad의 경량 U-Net 구조

- Streaming Inference

• Runtime memory와 user perceived latency를 줄이기 위해 streaming inference를 도입
  • Streaming Inference 과정
    1. Decoder input은 여러 consecutive phoneme들을 포함하기 위해 phoneme boundary에서 chunk로 잘림
       - Chunk length는 predefined 된 범위로 제한됨
    2. 이후 context information을 decoder에 반영하기 위해, 이전 chunk의 마지막 phoneme과 다음 chunk의 첫 번째 phoneme이 현재 chunk의 head, tail에 각각 pad 됨
    3. Decoder는 padding 된 각 chunk에 대해 mel-spectrogram을 생성
    4. Padding 된 phoneme에 해당하는 mel-spectorgram frame을 제거하여 각 chunk를 복원
  • 이를 통해, 생성된 음성에서 phoneme의 decoder input을 여러 chunk로 자름으로써 발생하는 noise를 방지할 수 있음
    - Padding된 phoneme은 decoder에 context information을 제공하여 더 자연스러운 prosody 생성을 도움

3. Experiment

- Settings

• Dataset : LJSpeech (English), Public Speech Dataset (Chinese)
• Comparison : Grad-TTS

- Results and Analysis

• Chinese dataset의 경우 LightGrad가 Grad-TTS 보다 더 우수한 합성 품질을 보임
  - English dataset에서는 Grad-TTS의 성능이 조금 더 높게 나왔으나 LightGrad의 품질과 크게 차이가 없었음
• Parameter와 latency 측면에서는, LightGrad가 Grad-TTS에 비해 62.2%의 parameter 절감과 65.7%의 latency 감소 효과를 보임
  - Runtime과 memory 측면에서도 LightGrad가 음성 품질의 큰 저하 없이 더 효율적인 성능을 보임

성능 비교 결과

- Ablation Study

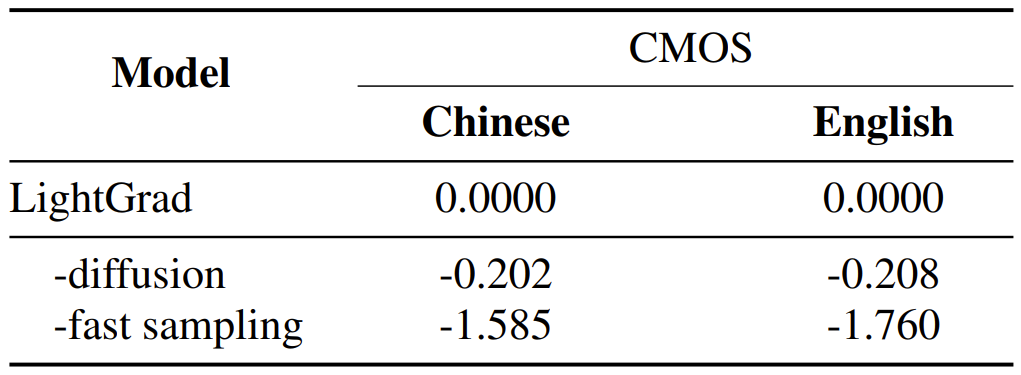
• Diffusion deocder를 4개의 Feed-Forward Transformer (FFT) block으로 구성된 deocder로 대체하고, Fast sampling을 Grad-TTS의 sampling으로 대체하여 성능을 비교
  • FFT decoder를 사용하면, noise가 더 많고 pronunciation 문제가 있는 부자연스러운 오디오가 생성되어 각각 -0.202, -0.208의 CMOS 저하가 발생
  • Fast sampling을 제거한 경우 각각 -1.585, -1.760의 CMOS 저하가 발생

Ablation study 결과