[Paper 리뷰] MixPath: A Unified Approach for One-shot Neural Architecture Search

MixPath: A Unified Approach for One-shot Neural Architecture Search

---

• 일반적인 two-stage neural architecture search method는 single-path search space에 제한되어 있음
• Multi-path structure를 효율적으로 search 하는 것은 여전히 어려움
• MixPath
  • Candidate architecture를 정확하게 평가하기 위해 one-shot multi-path supernet을 학습시킴
  • 서로 다른 feature statistics를 regularize하기 위해 Shadow Batch Normalization을 도입
  • 결과적으로 Shadow Batch Normalization을 통해 최적화를 안정시키고 ranking ability를 향상
• 논문 (ICCV 2023) : Paper Link

---

1. Introduction

• Neural Architecture Search (NAS) 방법론 중 one-shot 방식은 계산 비용을 크게 줄일 수 있음
  • 이러한 방법론들은 주로 weight-sharing mechanism을 활용한 single-path network search에 집중함
    - 이때 Inception, ResNeXT와 같은 multi-path structure는 성능 향상에 큰 도움이 될 수 있음
    - 따라서 search space에 multi-path structure를 통합하는 것이 필요
  • 이때 multi-path sub-model의 성능을 정확하게 예측하는 one-shot supernet을 학습시키기 위해서는 two-stage 방식을 필요로 함
    - Single-path의 경우 FairNAS의 fairness strategy를 적용하여 ranking difficulty를 크게 완화할 수 있음
    - 대신 multi-path에 대해서는 동일한 방법을 적용하기 어려움
  • Two-stage NAS를 활용하면 supernet이 sub-model의 ranking을 정확하게 예측할 수 있음
    - BUT, 이때 multi-path supernet은 sampling process 중에 statistics가 변함
    - 결과적으로 안정적인 rank를 제공할 수 없다는 단점이 존재

-> 그래서 multi-path supernet의 ranking 문제를 해결할 수 있는 unified NAS approach인 MixPath를 제안

 

• MixPath
  • 기존의 single-path 방식들과는 다른 multi-path one-shot NAS에 대한 unified approach를 제시
  • Vanilla multi-path training이 실패하는 원인을 분석하고, supernet을 안정화할 수 있는 Shadow Batch Normalization (SBN)을 도입
    
  • SBN 사용을 통해 multi-path supernet을 안정적으로 학습시키고 ranking 성능을 향상
  • 결과적으로 ImageNet에서 높은 성능의 architecture를 search 가능

< Overall of MixPath >

• One-shot multi-path NAS를 위한 unified approach
• 서로 다른 feature statistics를 regularize하기 위한 SBN의 도입
• SBN을 통해 multi-path supernet 최적화를 안정시키고 ranking ability를 향상

SBN을 통한 MixPath Supernet Training의 예시

2. MixPath: A Unified Approach

- Motivation 

• Multi-path one-shot NAS를 위한 효율적인 접근 방식이 필요함
  • Weight-sharing 방식은 stage level과 multi-path support 여부에 따라 4가지 category 분류될 수 있고, 이를 활용한 two-stage one-shot 방식은 supernet 학습을 위해 주로 single-path search space을 사용함
    -> 따라서 multi-path 방식에 대한 추가적인 one-shot NAS 방법론이 요구됨
  • Multi-path search space 설계시 고려사항
    1. Inception, ResNeXT와 같은 multi-path feature aggregation 방식의 유용함
    2. 성능과 계산 비용 사이의 적절한 trade-off
  • Inverted bottleneck이 $C_{in} \times H \times W$의 input feature를 가지고 각각 $C_{mid}, C_{out}$의 intermediate/output channel을 가진다고 가정하면,
    1. 총 계산 비용은 $c_{total} = 2HWC_{in}C_{mid}+k^{2}HWC_{mid} = 2HWC_{mid}(C_{in}+\frac{k^{2}}{2})$
       - $k$ : depth-wise convolution의 kernel size (일반적으로 3 or 5로 설정)
    2. 이때 $C_{in}$은 $\frac{k^{2}}{2}$를 dominate 하므로 무시가능한 비용으로 더 많은 kernel을 활용하여 depth-wise transformation의 representative power를 높일 수 있음
       -> 이러한 design은 MixConv와 ResNeX를 조합하는 것으로 고려할 수 있음

Weight-sharing NAS 방법론들의 분류

• Multi-path supernet은 학습하기 매우 어려움
  • Multi-path supernet에 대한 vanilla training은 상당히 어렵지만 single step에서 multi-path model을 random activate 하는 것으로 multi-path supernet을 학습하는 방식을 생각해 볼 수 있음
  • 이때 단순히 각 operation을 randomly acitivate/deactivate 하는 방식은 상당히 불안정함
    - 학습 안정성을 위해서는 다양한 operation의 feature에 대한 cosine similarity가 중요하기 때문
  • 실제로 학습된 supernet에서 다양한 feature의 cosine similarity matrix를 비교해 보면,
    1. Single-path feature 간의 similarity 외에도 multi-path와의 similarity도 같이 높게 측정됨
    2. Cosine similarity가 orientation 만을 측정하기 때문에 multi-path에 대해서는 부정확할 수 있음
    3. High-dimensional feature vector를 추가하면 angle를 크게 변경하지 않으면서 magnitude를 scale 할 수 있음
  • 결과적으로 여러 vector에 대한 superposition이 dynamic statistics를 만들어내므로 학습 불안정성이 유발됨 
    -> 이는 feature vector를 동일한 magnitude로 축소함으로써 안정화될 수 있음

Multi-path feature vector에 대한 Cosine Similarity, Projection

SBN 사용에 따른 학습 안정성 비교

- Regularizing Multi-path Supernet

• Dynamic statistics를 tracking 하기 위해 Batch Normalization (BN)을 사용할 수 있음
  • 다양한 $m$개 path에 대한 combination의 feature statistics를 standarad BN으로 regularization 하면,
    - Activated path combination을 shadow처럼 따르므로, 이를 Shadow Batch Normalization (SBN)이라고 함
  • Multi-path setting에서 모든 feature combination을 regularize 하기 위해서는 SBN 수가 exponential 하게 증가해야 함
    - $C^{1}_{m} + C^{2}_{m} + ... + C^{m}_{m} = 2^{m}-1$
• Reduce the Complexity from $2^{m}$ to $m$
  • Combination에 따른 SBN의 exponential 한 증가는 많은 비용을 필요로 하기 때문에 그 복잡도를 줄여야 함
    - 이를 위해 동일한 layer에 대한 서로 다른 operation의 output은 높은 similarity를 가진다는 점을 이용
    - 모든 single path의 feature (magnitude/angle)가 유사하다면 해당 combination도 비슷한 statistics를 가질 수 있으므로, SBN의 수를 $m$으로 줄일 수 있음
    
  • [Definition 1.] Zero-order condition
    두 개의 high-dimensional random variable $\mathbf{y} = \mathbf{f}(\mathbf{x}) \in \mathbf{R}^{\mathbf{M}\times \mathbf{d}_{1}}$과 $\mathbf{z} = \mathbf{g}(\mathbf{x}) \in \mathbf{R}^{\mathbf{M}\times \mathbf{d}_{1}}$가 있다고 하자. $\epsilon$이 매우 작은 양의 float number일 때, 모든 valid sample $\mathbf{x} \in \mathbf{R}^{\mathbf{N} \times \mathbf{d}}$에 대해, $|\mathbf{y}-\mathbf{z}|_{2} \leq \epsilon$을 만족한다면 $\mathbf{y}$와 $\mathbf{z}$는 zero-order condition을 만족한다고 한다.
  • [Lemma 3.1.]
    $\mathbf{m}$을 activable path의 최대 개수라고 하고, 각 operation pair는 zero-order condition을 만족한다고 할 때, $\mathbf{m}$개의 기댓값과 분산을 사용하여 모든 combination $2^{m}$을 근사할 수 있다.
    
  • 이때 $\epsilon$의 magnitude는 근사 오류에 큰 영향을 미치고 기댓값과 분산은 추가되는 개수에 따라 간단히 scale 될 수 있음:
    $\mathbb{E}[\mathbf{y}+\mathbf{z}] \approx \mathbb{E}[\mathbf{u}+\mathbf{v}] \approx 2\mathbb{E}[\mathbf{y}]$
    - [Lemma 3.1.]은 $i$ path를 포함하는 combination을 track 하기 위해 $SBN_{i} (i=1,2,...,m)$을 사용할 수 있음을 보장
• Statistical Analysis of Shadow Batch Normalization
  • Search space $S_{1}$에 대해 CIFAR-10에서 학습된 supernet의 statistics를 비교
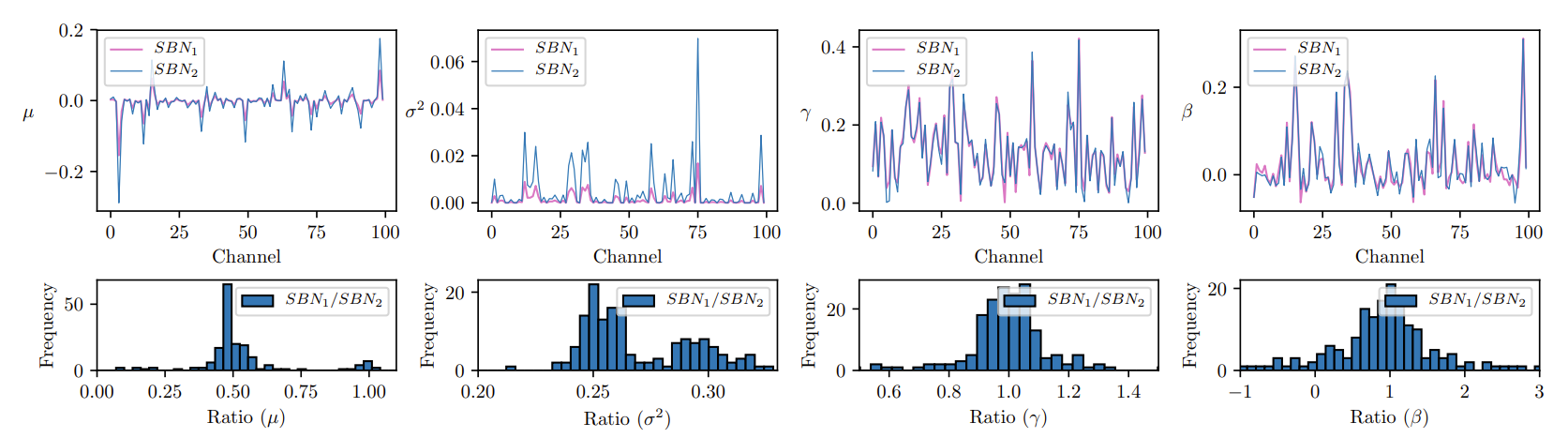
    - $m=2$로 설정하고 첫 번째 선택 block에 대해 모든 channel에서 SBN의 4개 parameter에 대한 statistics를 수집
    - $SBN_{1}$은 one-path에 대한 statistics를 caputre 하고, $SBN_{2}$는 two-path에 대한 statistics를 capture
  • [Lemma 3.1.]을 통한 이론적 근사에 따라, 실험에서 $\mu_{bn_{1}} \approx 0.5\mu_{bn_{2}}$, $\sigma^{2}_{bn_{1}} \approx 0.25 \sigma^{2}_{bn_{2}}$이 나타나야 함
    - 이러한 현상은 아래 그림의 $\mu, \sigma^{2}$에 대한 그래프를 통해 일관되게 관찰됨
    - 추가적으로 learnable parameter $\beta, \gamma$가 $SBN_{1}, SBN_{2}$와 상당히 유사함을 보임
    - SBN이 서로 다른 statistics를 유사한 분포로 변환하여 $\beta, \gamma$의 parameter가 매우 가까워지기 때문

CIFAR-10에서 학습된 MixPath Supernet의 SBN parmaeter들에 대한 statistics

- MixPath Neural Architecture Search

• 위의 분석을 기반으로 SBN을 활용해 multi-path supernet인 MixPath supernet을 학습
  • Supernet은 one-shot 방식을 통해 pre-defined search space에서 모델을 평가하는 데 사용되어 two-stage pipeline으로 동작함
    
    1. SBN을 사용한 supernet training
       - 이때 training stage에서 각 step 별로 여러 path가 activate 되어 mixed output을 만들어낼 수 있도록 random sampling을 적용
    2. Competitive model search
       - NSGA-II와 같은 evolutionary algorithm을 적용하여 search를 진행
  • 이때 MixPath는 FLOPs를 최소화하면서 classification accuracy를 최대화하는 것을 목표로 함
    - 추가적으로 orthogonal post-processing trick인 batch normalization calibration을 활용하여 ranking ability를 개선

MixPath Supernet Training Algorithm

3. Experiments

- Settings

• Dataset & Search Space
  - CIFAR-10의 경우 : 12개의 inverted bottleneck block이 포함된 $S_{1}$을 search space로 사용
  - ImageNet의 경우 : MnasNet, MixNet과 유사한 $S_{2}, S_{3}$ search space를 사용
  - Kendall Tau 분석용 : NAS-Bench-101의 subset인 $S_{4}$를 사용
• Comparisons : NASNet, ENAS, DARTS, RDARTS, SNAS 등

- Results

• Ranking Ability Analysis on NAS-Bench-101
  • SBN이 supernet 학습을 안정화하고 ranking ability를 향상할 수 있음을 확인하기 위해 NAS-Bench-101에 대한 실험을 수행
  • SBN으로 학습된 supernet은 SBN을 사용하지 않았을 때 보다 더 우수한 ranking ability를 보임
    - 특히 Kendall Tau를 개선할 수 있는 BN post-calibration이 적용된 vanilla BN 보다 더 우수한 ranking ability를 보임
    - SBN과 BN post-calibration을 모두 사용하는 경우 0.597까지 성능이 향상됨

SBN 적용 여부에 따른 Kendall Tau 비교

 

(a) NAS-Bench-101에 SBN을 적용한 Search Space (b) Supernet Accuracy와 Ground-Truth 간의 Kendall Tau

• Search on CIFAR-10
  • CIFAR-10 dataset에서 $S_{1}$ search space를 대상으로 MixPath를 적용하여 최적의 architecture를 search
  • Searched architecture인 MixPath-c는 493M FLOPs와 97.4%의 top-1 accuracy를 달성

CIFAR-10에서의 결과

• Proxyless Search on ImageNet
  • ImageNet에 대해 $S_{2}, S_{3}$ search space를 사용하여 최적의 architecture를 얻음
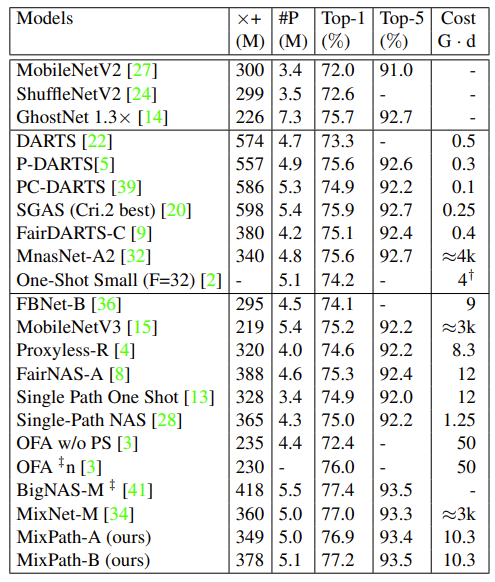
  • $S_{3}$의 Pareto-front에서 sample 된 MixPath-A는 ImageNet에서 349M의 multiply-add를 사용하면서 76.9%의 accuracy를 달성
  • $S_{2}$로 얻어진 MixPath-B는 EfficientNet 보다 더 적은 수의 FLOPs를 사용하면서 77.2%의 accuracy를 달성

ImageNet에서의 결과

- Ablation Study

• Supernet Ranking with Different Strategies
  • SBN과 BN post-calibration의 기여도를 확인하기 위해 NAS-Bench-101을 활용하여 Kendall Tau를 비교
  • Supernet with and without SBNs
    - SBN 없이 학습된 supernet은 낮은 Kendall Tau ($\tau=0.05$)를 보여 모델 평가에 부적절한 것으로 나타남
    - BN calibration이 적용되면 $\tau$가 향상됨을 확인 가능
    - 결과적으로 SBN과 BN post-calibration을 모두 사용했을 때 최고의 성능을 발휘함
  • Linear number of SBNs vs. exponential
    - SBN은 이론적으로 combination에 대해 linear 한 증가를 보이지만, 모든 single combination에 대해 exponential counterpart를 사용할 수 있음
    - Calibration이 적용된 Linear SBN (LSBN)은 가장 높은 $\tau$값을 보였지만, Exponential SBN (ESBN)에는 효과적이지 않은 것으로 나타남
    - ESBN은 learnable parameter $\beta, \gamma$의 분포를 더 넓게 만들어 BN calibration의 적용이 어렵기 때문 

SBN ablation에 대한 Kendall Tau 비교

• One-shot Accuracy Distribution of Candiate Models
  • 각 $m=1,2,3,4$ path에 대한 CIFAR-10의 test accuracy 분포를 확인
  • $m=1$인 경우 MixPath는 single-path를 사용할 수 있지만 SBN은 $m>1$에 대해 뚜렷한 효과를 보임
    -  $m>1$이 아니면 accuracy가 낮고 large gap을 가지는 supernet이 생성됨
    - 결과적으로 SBN이 없는 supernet의 경우, architecture의 성능을 과소평가할 수 있음

$m$ path별 MixPath Supernet에서 One-shot Sample된 Model의 Accuarcy 비교

• Simple Scaling vs. SBNs
  • 각 block의 feature magnitude를 동일하게 scaling 함으로써 supernet 학습을 안정화할 수 있음
  • Simple scaling을 사용했을 때 ranking ability는 vanilla BN이나 Exponential SBN보다 높지만, Linear SBN 보다는 낮음

Simple Scaling과 SBN의 비교

• Applying SPOS on Multi-path Search Space
  • NAS-Bench-101에서 3개의 candidate operation을 사용하여 branch composition을 실험
  • 해당 search space에 SPOS를 적용했을 때, Kendall Tau 값은 -0.225로 측정됨
    - 그에 비해 MixPath는 0.504의 Kendall Tau 값을 얻음
  • 이는 SPOS는 MixPath supernet 보다 4배 더 많은 learnable parameter를 사용하기 때문 (199.7M vs. 52.9M)
    - 결과적으로 SPOS가 candidate block을 완전히 최적화하는 것을 실용적으로 불가능하게 함

SPOS와 MixPath의 Kendall Tau 비교