[Paper 리뷰] AutoDiffusion: Training-Free Optimization of Time Steps and Architectures for Automated Diffusion Model Acceleration

AutoDiffusion: Training-Free Optimization of Time Steps and Architectures for Automated Diffusion Model Acceleration

---

• Diffusion model은 이미지 생성을 위해 많은 수의 time step을 필요로 함
• 서로 다른 model은 추론 시간을 가속화하는 서로 다른 최적의 time step을 가질 수 있음
• AutoDiffusion
  • 추가적인 학습 없이 diffusion model에 대한 최적의 time step과 architecture를 search 가능
  • 가능한 모든 time step과 다양한 architecture에 대한 unified search space 구성
  • 최적의 solution을 찾기 위한 two-stage evolutionary search를 도입
  • Search process를 가속화하는 FID score 기반의 성능 추정
• 논문 (ICCV 2023) : Paper Link

---

1. Introduction

• Diffusion model은 diffusion process를 활용하여 input data에 noise를 점진적으로 추가하여 Gaussian 분포로 변환하고, sampling 된 noise로부터 data를 복원하는 reverse process를 수행
  • 결과적으로 exact likelihood 계산을 통해 우수한 sample 합성 품질을 달성할 수 있음
  • BUT, diffusion model은 합성 속도가 상당히 느림
    - i.g.) V100 GPU에서 StyleGAN은 0.015초가 걸리지만 ADM은 14.75초가 걸림
• Diffusion model의 생성 속도를 개선하기 위해, 주로 time step 수를 줄이는 방식을 활용함
  • Time step을 줄이기 위해 주로 특정 procedure를 활용하거나 uniform하게 새로운 time step을 sampling 함
    - 합성 과정을 Stochastic Differential Equation (SDE)나 Ordinary Differential Equation (ODE)로 표현하여 수치해석을 적용하는 방식
    - Knowledge-Distillation을 활용하는 방식
  • BUT, 주어진 diffusion model에 대해 적합한 length를 가지는 최적의 time step sequence가 존재함
    - 이때 최적의 time step sequence는 특정한 task와 diffusion model의 hyperparameter에 따라 달라짐
  • 따라서, original time step을 최적의 time step으로 대체함으로써 diffusion model의 합성 품질을 향상할 수 있음

-> 그래서 diffusion model에 대해 최적의 time step과 architecture를 동시에 search하는 AutoDiffusion을 제안

 

• AutoDiffusion
  • Neural Architecture Search (NAS)에서 영향을 받아 neural network를 압축
  • Pre-trained diffusion model과 원하는 time step 수에서 시작하여, 가능한 모든 time step sequence와 noise prediction network architecture로 구성된 unified search space를 구성
  • Search space를 효과적으로 탐색하기 위해 two-stage evolutionary search를 도입하고, FID score를 metric으로 하여 candidate time step과 architecture에 대한 성능을 추정
  • AutoDiffusion으로 search 된 결과는 search process를 반복하지 않고도 동일한 guidance scale 하에서 다른 model로 확장 가능

< Overall of Paper >

• Uniform sampling, fixed function을 활용하지 않고 각 diffusion model에 대한 time step sequence와 noise prediction architecture를 모두 포함하는 search space를 구성
• 주어진 search space에서 최적의 time step과 architecture를 search 하는 training-free framework
• 앞선 diffusion model과 비교하여 2배의 추론 속도 향상과 few time step만으로도 우수한 성능을 달성

AutoDiffusion의 필요성

2. Diffusion Models

• 미지의 분포 $p_{data} (x_{0})$에서 sampling 된 variable $x_{0} \in \mathbb{R}^{D}$가 주어지면,
  • Diffusion model은 $T$ diffusion step을 통해 data $x_{0}$를 sample $x_{T}$로 변환하는 diffusion process $\{ x_{t} \}_{t \in [0:T]}$를 정의
    - 이때, sample $x_{T}$의 분포 $p(x_{T})$는 standard Normal 분포와 같이 tractable 한 분포
  • Diffusion process에서 time step $t$에 대한 variable $x_{t}$의 분포는:
    (Eq. 1) $q(x_{t}|x_{0}) = \mathcal{N} (x_{t} | \alpha_{t} x_{0}, \beta^{2}_{t} I)$
    - $\{ \alpha_{1}, \alpha_{2}, ..., \alpha_{T} \}, \{ \beta_{1}, \beta_{2}, ..., \beta_{T} \}$ : $x_{0}$를 $x_{T}$로 변환하는 속도를 제어하는 diffusion model의 hyperparameter
  • Neural network $\theta$에 의해 parameterize 되고 log Evidence Lower BOund (ELBO)에 의해 최대화되는 reverse process $p_{\theta} (x_{t-1} | x_{t})$는:
    (Eq.2) $L_{elbo} = \mathbb{E} [log \, p_{\theta} (x_{0}|x_{1}) - \sum_{t=1}^{T} D_{KL} ( q(x_{t-1} | x_{t}, x_{0}) || p_{\theta} (x_{t-1} | x_{t}) ) - D_{KL} ( q(x_{T} | x_{0}) || p(x_{T}) ) ]$
    - $D_{KL}$ : KL-Divergence
• Diffusion model은 noise prediction network $\epsilon_{\theta} (x_{t}, t)$를 통해 time step $t$에서 noisy sample $x_{t}$의 noise component를 추정
  • 이때, (Eq. 2)의 loss function은 아래와 같이 단순화할 수 있음:
    $L_{simple} = || \epsilon_{\theta} (x_{t}, t) - \epsilon ||^{2}$
    - $\epsilon$ : $x_{t}$의 noise component이고, $x_{t}$는 (Eq. 1)로부터 $x_{t} = \alpha_{t} x_{0}$로 얻어짐 
    - 대부분의 diffusion model에서 noise $\epsilon$은 noisy sample $x_{t}$를 생성할 때 standard Normal 분포 $\mathcal{N} (0, I)$로 sampling 됨
  • Noise prediction network $\epsilon_{\theta}(x_{t}, t)$가 학습되면 diffsuion model은 sample을 얻기 위한 generation process를 수행
    - Generation process는 $p(x_{T})$에서 sampling 되는 noisy data에서 시작하여 학습된 분포 $p_{\theta} (x_{t-1} | x_{t})$를 통해 sample $x_{T-1}, x_{T-2}, ..., x_{0}$를 점진적으로 cleaning 함
  • Generation process에서 최종적인 sample $x_{0}$를 얻기 위해서는, noise prediction network $\epsilon_{\theta}$에 대한 적절한 $T$가 필요함
    - 이 time step $T$를 $K < T$로 줄이는 방법들이 제시되었지만, 대부분 최적의 time step을 sampling 하지 못함
    - i.g.) DDIM은 $[0, \frac{T}{K}, ..., \frac{KT}{K}]$와 같이 length $K$를 가지는 linear time step sequence를 활용
  • 따라서 AutoDiffusion은 diffusion model에 대한 $K$ length의 최적 time step sequence를 search 하는 것을 목표로 함

Overall of AutoDiffusion

3. Method

- Motivation

• Diffusion model의 generation process는 여러 단계로 나누어져 있고, 각 단계마다 diffusion model의 동작이 다름
  • 각 단계는 Coarse feature, Perceptually rich content, Removing remaining noise로 분류될 수 있음
    - 즉, diffuison model의 denoising 난이도는 time step에 따라 달라짐
  • 따라서 generation process에서 각 time step의 중요성이 다르므로, diffusion model에 대한 최적의 time step sequence가 존재할 수밖에 없음
• 이를 확인해 보기 위해 sample $x_{t}$를 얻고, 각 time step $t$에 대해 Mean Squared Error (MSE) $|| x_{t} - x_{t+100} ||^{2}$을 비교
  • 아래 그림을 보면,
    1. $t \in [600, 1000]$에 대해 얻어지는 sample은 noise로 인해 illegible 함
    2. $t \in [300, 600]$이면, diffusion model은 이미지의 주요 content를 생성하고, 인식 가능한 객체를 만들어냄
    3. $t \in [0, 300]$에서는, diffusion model은 denoising을 수행하고, $t \in [0,300]$에 대한 유사한 sample을 만들어냄
    4. MSE는 $t \in [0, 100], t \in [700,900]$에서 낮고, $t \in [200, 600]$에서는 높게 나타남
       
  • 위 결과처럼 diffusion model의 generation process에서 각 time step은 서로 다른 역할을 수행함
    - $t$가 작거나 크면 생성된 sample이 천천히 변화하고, $t$가 중간의 값을 가지면 급격한 변화를 보임
  • 따라서 diffusion model은 time step에 따라 uniform 하게 변하는 것이 아니므로, 최적의 time sequence를 search 할 수 있어야 함
    - 이때 denoising 난이도 역시 time step에 따라 변화하므로 noise prediction network의 크기가 반드시 동일할 필요는 없음

 

Time Step $t$에 대한 sample과 MSE 변화

- Search Space

• AutoDiffusion의 search space를 정의
  • Time step $[t_{1}, t_{2}, ..., t_{T}] (t_{i} < t_{i+1})$를 가지는 diffusion model이 주어졌을 때,
    - 이미지 batch를 생성하기 위해서는, noise prediction network $\epsilon_{\theta}$를 $T$번 호출해야 함
  • 이때, generation process를 가속화하기 위해 2가지 방법을 사용할 수 있음
    
    1. Time step 수를 줄이거나
       
    2. $\epsilon_{\theta}$의 layer 수를 줄이거나
  • 따라서 AutoDiffusion은 2개의 orthogonal component로 구성된 search space를 도입
    
    1. Time step에 대한 temporal search space
    2. Noise prediction network $\epsilon_{\theta}$의 architecture에 대한 spatial search space
  • 이때, search space에서 candidate $cand$는:
    (Eq. 4) $cand = \{ \mathcal{T} = [t_{1}^{'}, t_{2}^{'}, ..., t_{K}^{'} ]; \mathcal{L} = [L_{1}, L_{2}, ..., L_{K}] \},$
    $0 < t_{i+1}^{'} - t_{i}^{'} < t_{T} - t_{1}, t_{i}^{'} \in [ t_{1}, t_{2}, ..., t_{T} ] (i=1,2,...,K)$
    - $\mathcal{T}$ : sampled time step sequence, $\mathcal{L}$ : sampled architecture
    - $[t_{1}^{'}, t_{2}^{'}, ..., t_{K}^{'}]$ : original time step sequence $[t_{1}, t_{2}, ..., t_{T}]$의 sub-sequence
    - $L_{i} = [l_{i}^{1}, l_{i}^{2}, ..., l_{i}^{n_{i}}]$ : time step $t_{i}^{'}$에서 noise prediction network $\epsilon_{\theta}$의 layer로, $L_{i}$는 $\epsilon_{\theta}$의 sub-network
  • 각 time step에서 model layer의 합을 $N_{max}$이하로 제한
    - $\sum_{i=1}^{K} n_{i} \leq N_{max}$이고, $N_{max}$는 diffusion model의 예상 생성 속도에 따라 결정됨
• AutoDiffusion은 unified framework를 활용하여 최적의 time step sequence와 noise prediction model을 search 함
  • 시간적인 측면에서 가능한 모든 time step 중에서 최적의 time step sequence를 search
  • 공간적인 측면에서 각 time step에서 noise prediction network의 layer를 search
  • 이때, sub-network $L_{i}$는 search 과정에서 모든 time step에 대해 동일하지 않을 수 있음
    - 이는 denoising의 난이도가 time step에 따라 서로 다르기 때문
    - 따라서 각 time step $t_{i}^{'}$의 layer 수 $n_{i}$가 $t_{i}^{'}$에서의 denoising 난이도를 반영한다고 볼 수 있음
  • Noise prediction network $\epsilon_{\theta}$는 U-Net을 활용
    - Search space에 up/down sampling layer가 추가되지 않음
    - Candidate에서 model layer가 선택되지 않는 경우, layer는 skip connection으로 대체됨
  • 추가적으로 search 된 $\epsilon_{\theta}$의 sub-network는 fine-tuning 되거나 re-training 되지 않음

- Performance Estimation

• Search space가 결정되면, search process에 대한 빠르고 적절한 성능 추정을 제공하기 위한 metric을 선정해야 함
  • 이때 metric으로 고려할 만한 것은:
    1. 학습된 분포 $p_{\theta}(x_{t_{i-1}} | x_{t_{i}})$와 posterior $q(x_{t_{i-1}} | x_{t}, x_{0})$ 사이의 거리
       
    2. 생성된 sample과 실제 sample 사이의 statistics 간의 거리
  • 분포 $p_{\theta}(x_{t_{i-1}} | x_{t_{i}})$와 posterior $q(x_{t_{i-1}} | x_{t}, x_{0})$ 사이의 거리는 일반적으로 KL-divergence로 추정됨
    - 따라서, 정렬된 candidate time step $[t_{1}^{'}, t_{2}^{'}, ..., t_{K}^{'}]$에 대해 KL-divergence를 계산을 통한 성능 추정은:
    (Eq. 5) $L = L_{t_{1}^{'}} + L_{t_{2}^{'}} + ... + L_{t_{K}^{'}}$
    $L_{t_{i}^{'}} = \left \{ \begin{matrix} D_{KL} ( q(x_{t_{i}^{'}}|x_{0}) || p(x_{t_{i}^{'}}) ), \quad \quad \quad \quad \quad \quad t_{i}^{'} = t_{T} \\ - log \, p_{\theta} ( x_{t_{i}^{'}} | x_{t_{i+1}^{'} }  ), \quad \quad \quad \quad \quad \quad \quad \quad t_{i}^{'} = 0 \\ D_{KL} ( q(x_{t_{i}^{'}} | x_{t_{i+1}^{'}}, x_{0}) || p_{\theta} ( x_{t_{i}^{'}} | x_{t_{i+1}^{'}} )  ), \quad others \end{matrix} \right .$
  • 학습된 diffusion model이 주어지고, training dataset에서 sample 된 이미지 $x_{0}$와 candiate time step $[t_{1}^{'}, t_{2}^{'}, ..., t_{K}^{'}]$가 주어지면, (Eq. 5)로부터 KL-Divergence를 계산하여 성능 추정을 빠르게 수행할 수 있음

• BUT, KL-divergence로 최적화를 수행해도 sample 품질이 향상되지 않을 수 있음
  • 이를 위해 FID, sFID, IS, Precision, Recall와 KL-divergence 간의 Kendall-tau를 계산하여 관련성을 비교
    - ImageNet $64 \times 64$에서 학습된 diffusion model의 time step sequence $[t_{1}, t_{2}, .. t_{T}]$를 search space로 구성하고,
    - 해당 search space에서 sub-sequence $[t_{1}^{'}, t_{2}^{'}, ..., t_{K}^{'}]$를 무작위로 sampling 하여 Kendall-tau를 계산
  • 결과적으로 모든 metric과 KL-divergence 간의 Kendall-tau 값이 낮음
    - KL-divergence는 sampling 품질을 올바르게 대표할 수 없음

여러 metric들과 KL-divergence 간의 Kendall-tau 비교

• 생성된 sample과 실제 sample 간의 거리는 KID나 FID를 통해 추정할 수 있음
  • 따라서 FID를 KL-divergence 대신 성능 추정 metric으로 사용:
    (Eq. 6) $Score = || m_{r} - m_{g} ||_{2}^{2} + Tr (C_{r} + C_{g} - 2(C_{r}C_{g})^{\frac{1}{2}})$
    - $m_{r}, m_{g}$ : 각각 실제 sample과 생성된 sample의 feature에 대한 평균
    - $C_{r}, C_{g}$ : 각각 실제 sample과 생성된 sample의 feature에 대한 공분산
    - 이때, 각 sample에 대한 feature는 pre-trained VGG model로부터 얻어짐
  • 정확한 FID를 계산하기 위해서는 최소한 10k의 sample을 생성해야 하므로 search 속도가 느려짐
    - 이를 위해 FID 계산에 필요한 sample 수를 줄여야 함
  • Kendall-tau를 적용하여 감소된 sample 수를 결정
    1. Full time step sequence $[t_{1}, t_{2}, ..., t_{T}]$를 search space로 사용하고, $N_{seq}$개의 sub-sequence $[t_{1}^{'}, t_{2}^{'}, ..., t_{K}^{'}]$를 무작위로 sample
    2. 이후 각 sub-sequence를 사용하여 50k의 sample을 생성하고, 해당하는 FID $\{ F_{1}, F_{2}, ..., F_{N_{seq}} \}$를 얻음
    3. 다음으로, 50k 개의 sample에서 $N_{sam}$개의 subset을 얻고, 해당하는 FID $\{ F_{1}^{'}, F_{2}^{'}, ..., F_{N_{seq}^{'}} \}$를 계산
    4. 마지막으로  $\{ F_{1}, F_{2}, ..., F_{N_{seq}} \}$와 $\{ F_{1}^{'}, F_{2}^{'}, ..., F_{N_{seq}^{'}} \}$ 사이의 Kendall-tau를 계산
  • 결과적으로 최적의 sample 수는 Kendall-tau를 0.5 보다 크게 만드는 최소의 $N_{sam}$

- Evolutionary Search

• Search space에서 가장 적합한 candidate를 선정하기 위해 Evolutionary Search를 활용
  • Evolutionary search는:
    1. 학습된 diffusion model이 주어지면 (Eq. 4)에 따라 search space에서 무작위로 candidate를 sampling 하여 초기 모집단을 생성
    2. 이후 생성된 sample을 기반으로 FID score를 계산
    3. 각 반복에서 FID가 가장 낮은 상위 $k$개의 candidate를 parent로 선택
    4. 선택된 parent에 대해 crossover와 mutation을 적용하여 새로운 모집단을 생성
       - Crossover는 두 상위 candidate 간의 time step과 model layer를 무작위로 교환
       - Mutation은 선택된 상위 candidate에서 확률 $p$에 따라 time step과 model layer를 수정
  • AutoDiffusion에서는 two-stage evolutionary search를 활용
    - Evolutionary search의 처음 몇 번의 반복에 대해서만 full noise prediction network와 time step을 사용
    - 나머지 search process에서 time step과 model architecture를 공동으로 search

3. Experiments

- Settings

• Dataset : LSUN dataset
• Comparisons : ADM/ADM-G, DDIM, PLMS, DPM-Solver, Stable Diffusion

- Results

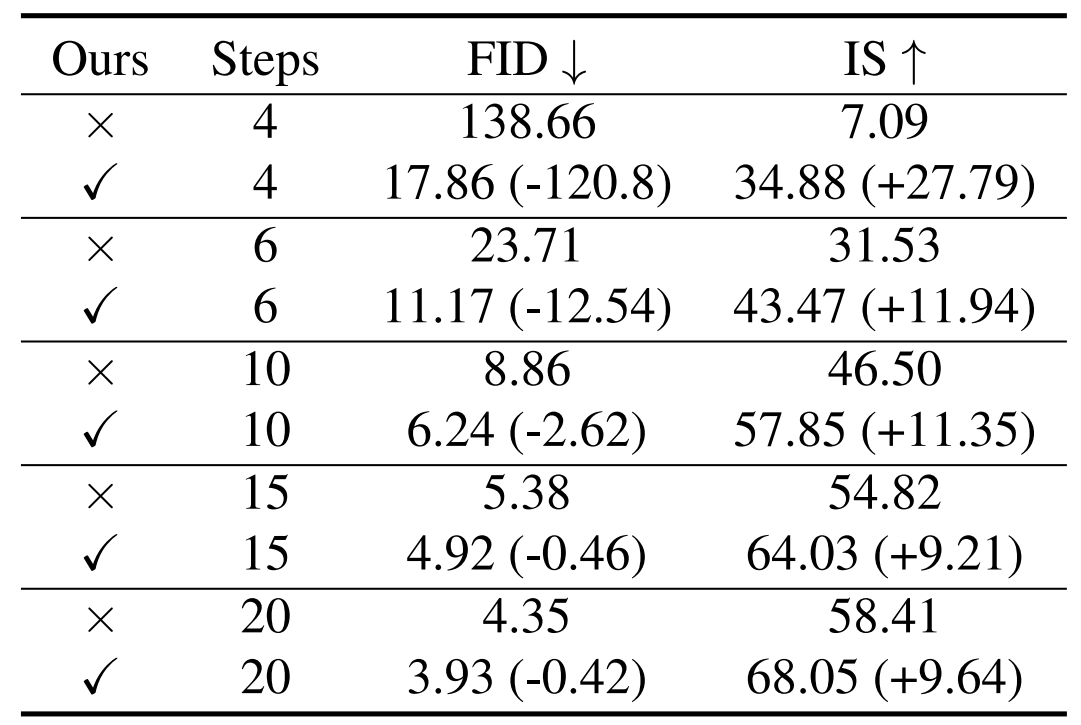
• AutoDiffusion을 적용하면 다른 diffusion model들에 비해 time step이 매우 적을 때 압도적인 성능을 보임
  - 특히 4-step에서 ADM-G는 138.66 FID를 보였지만 AutoDiffusion은 17.86 FID를 달성

ADM-G와 AutoDiffusion 비교

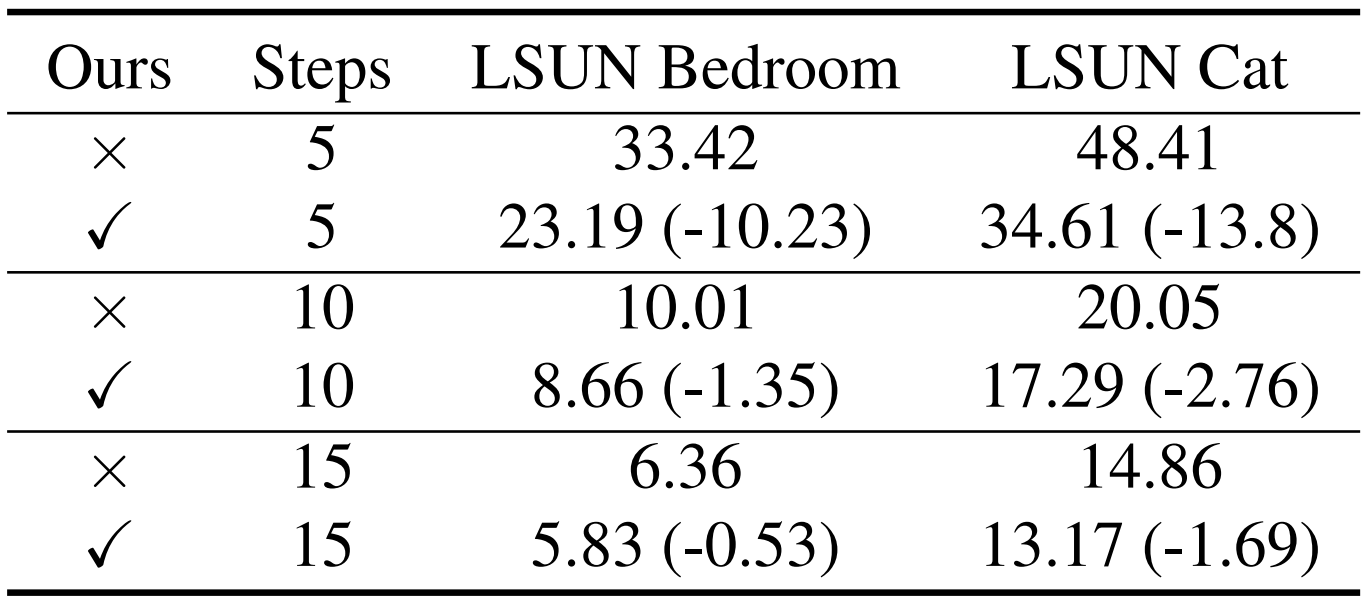
• LSUN dataset에 대해서도 AutoDiffusion은 적은 time step 만으로도 우수한 품질의 sample을 합성할 수 있음

LSUN dataset에서 ADM과 AutoDiffusion 비교

• AutoDiffusion을 DPM-Solver, DDIM, PLMS에 각각 적용해 보면,
  - 마찬가지로 낮은 time step에 대해서 sample 합성 품질을 크게 향상할 수 있음
  - 특히 AutoDiffusion을 적용하지 않았을 때에 비해 2배나 빠른 10-step 만에 최고 성능을 달성 

Time step별 FID 비교

• 합성된 sample을 확인해 보면, AutoDiffusion으로 생성된 sample은 다른 방법들보다 더 명확하게 detail을 표현함
• Step = 10에서 AutoDiffusion으로 합성된 이미지와 Step = 20에서 DPM-Solver 만으로 합성된 이미지가 서로 유사
  - 결과적으로 AutoDiffusion은 2배 빠르게 같은 품질의 이미지를 합성 가능

합성된 sample 비교

AutoDiffusion과 DPM-Solver 비교

- Migrate Search Results

• AutoDiffusion을 사용하여 ImageNet $64 \times 64$에서 guidance scale 1.0과 7.5에서 ADM-G에 대한 length 4의 time step을 가지는 최적의 sequence를 search
  - 각 guidance scale에서 ADM-G로부터 search 된 time step의 분포는 크게 다르게 나타남
• 동일한 guidance scale을 가지는 새로운 diffusion model이 주어지면 AutoDiffusion은 search process를 반복하지 않고도 원하는 time step sequence를 얻을 수 있음
  - 7.5 guidance scale로 얻어진 ADM-G의 최적 time step을 활용하면 24.11 FID를 얻을 수 있음
  - 이를 Stable Diffusion에 도입하면 최적 time step은 FID를 38.25에서 20.93으로 향상할 수 있음
• BUT, 서로 다른 guidance scale을 가진 diffusion model에 대해서는 search 된 결과가 transfer되지 않음
  - i.g.) Guidance 7.5 Stable Diffusion의 결과를 guidance 1.0의 ADM-G에 적용하는 경우

(a) Guidance scale 1.0 (b) Guidance scale 7.5 에서 Evolutionary Search의 top-10 candidate 수

- Search for Time Steps and Architecture

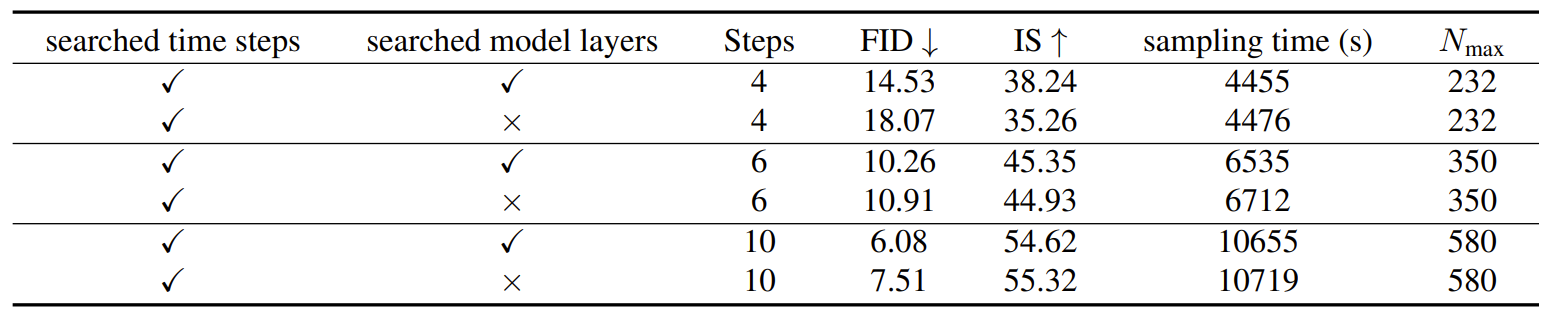
• AutoDiffusion을 time step과 model layer에 대해 함께 적용하면 성능을 더욱 향상할 수 있음
  - 이를 통해 search된 diffusion model은 FID 및 합성 속도 측면에서 기존보다 우수한 성능을 보임
  - Search 된 architecture를 보면, residual block과 attention block은 모두 작은 time step length에서 필수적으로 사용됨
  - 다만 step이 늘어날수록 attention block의 중요도가 커짐

Time step과 model layer에 대해 search된 model의 성능 비교

- Comparison to the Prior Work

• Differentiable Diffusion Sample Search (DDSS)와 AutoDiffusion을 비교해 보면, AutoDiffusion이 더 나은 FID와 IS를 보임

DDSS와의 비교

- The Efficiency of AutoDiffusion

• 계산 효율성 측면에서, AutoDiffusion은 training-free search를 통해 우수한 효율성을 보임
  - DDSS와 비교하여 3.15배의 효율성 향상

계산 효율성 비교