[Paper 리뷰] AutoNF: Automated Architecture Optimization of Normalizing Flows with Unconstrained Continuous Relaxtion Admmitting Optimal Discrete Solution

AutoNF: Automated Architecture Optimization of Normalizing Flows with Unconstrained Continuous Relaxtion Admitting Optimal Discrete Solution

---

• 강력하면서도 계산 효율적인 flow model을 구축하는 것은 여전히 어려움
• 이를 위해 Neural Architecture Search를 고려할 수 있지만, Normalizing Flow의 invertibility constraint로 인해 기존 방식들은 적용하기 어려움
• AutoNF
  • Normalizing Flow에 대한 automated architectural optimization framework
  • Flow model의 invertibility constraint를 violating 하지 않으면서 효율적인 differentiable architecture search를 지원하는 mixture distribution formulation을 제시
  • 해당 formulation을 기반으로 NP-hard architecture optimization 문제를 discrete optimal solution을 허용하는 unconstrained continuous relaxtion으로 변환
    - 이를 통해 architectural optimization에서 binarization으로 인한 optimality 손실을 회피
• 논문 (AAAI 2023) : Paper Link

---

1. Introduction

• Normalizing Flow (NF)는 tractable Jacobian을 통한 bijection을 기반으로 구축된 invertible neural network
  • 이러한 flow model은 복잡한 분포에서 exact density estimation과 sampling을 허용함으로써, generative model 등에서 우수한 성능을 보이고 있음
    - 이때 optimal flow model은 다양한 환경에 따라 크게 달라질 수 있으므로, 성능과 계산 비용 간의 trade-off가 발생함
  • 이를 해결하기 위해 다양한 bijection들이 제안되고 있지만, 여전히 성능과 계산 비용 모두에서 optimal 한 single bijection은 존재하지 않음
    - Expressive flow는 forward/inverse pass에서 computational overhead가 증가하거나 analytical invertibility를 잃는 경향이 있음
    - 한편으로 빠른 속도의 flow는 rich한 분포를 모델링할 수 없으므로 성능의 한계가 있음

• 특히 대부분의 flow model은 큰 design space에도 불구하고, 수동으로 설계됨
  
  • 따라서 flow model을 optimize 하기 위해 자동화된 방식인 Neural Architecture Search (NAS)를 고려할 수 있음
    1. BUT, unstructured neural network의 optimization을 위한 differentiable-NAS (D-NAS)는 invertibility를 유지할 수 있는 mechanism이 없기 때문에 NF에 직접 적용할 수 없음
    2. 특히 unstructured neural network에서 discrete architecture solution을 얻기 위해 optimized relaxed continuous solution을 binarizing 하면, differential NAS의 optimality가 손상될 수 있음
  • 결과적으로 위의 한계점들로 인해, NF architecture에 대한 NAS 방법론은 아직까지 제시되지 않음

-> 그래서 NF에 대한 differentiable NAS를 가능하게 하는 AutoNF를 제안

 

• AutoNF
  • Optimized flow model의 invertibility를 보장하면서 differentiable architecture search를 수행할 수 있는 새로운 mixture distribution formulation을 제안
  • 기존 NP-hard combinational architectural optimization 문제를 discrete optimal architectural solution으로 admitting 하는 unconstrained continuous relaxtion으로 변환
    - 이를 통해 architectural optimization에서 binarization으로 인한 손실을 방지

< Overall of AutoNF >

• NF의 invertibility constraint를 준수하는 differentiable NAS 방법론
• Discrete optimal solution을 허용하는 unconstrained continuous relaxtion으로 변환하여 optimal 한 탐색을 허용
• 결과적으로 AutoNF로 탐색된 결과는 기존의 flow model들보다 훨씬 계산 효율적이면서도 우수한 성능을 보임

2. Preliminaries

- Normalizing Flows

• Normalizing Flow는 두 random variable 사이의 bijection을 optimizing 하여 복잡한 분포를 모델링함
  • Output/input random variable $x, u$와 그에 해당하는 분포 $p_{x}(x), p_{u}(u)$가 주어진다고 하자
  • $u=T_{\theta}(x)$와 같이 $x$를 $u$로 변환하는 bijection $T_{\theta}$가 있는 경우, $x$의 density function은:
    (Eq. 1) $p_{x}(x)=p_{u}(T_{\theta}(x))\cdot | \det(J_{T_{\theta}}(x))|$
    - 여기서 편의 상, $T^{-1}$ 대신 $T$를 inverse transform으로 나타냄
    - $\det(J_{T_{\theta}}(x))$ : inverse transform $T_{\theta}$의 Jacobian determinant

• Flow model의 expressive power는 bijection을 multiple layer로 stacking 하여 향상할 수 있음
  • Output/input random variable이 각각 $x_{n^{2}}, x_{0}$인 $n$-layer flow model은, $n$개의 transformation ($T_{1}, T_{2}, ..., T_{n}$)을 $x_{0}=T_{1}\circ T_{2}...\circ T_{n}(x_{n})$이 되도록 sequential 하게 적용한 것
  • 이때 $i$-th transformation ($i\in[1,n]$) 이후의 density function은:
    (Eq. 2) $p_{x_{i}}(x_{i})=p_{x_{i-1}}(T_{i}(x_{i}))\cdot | \det J_{T_{i}}(x_{i})|$
  • 각 layer에 (Eq. 2)를 적용하면 아래의 (Eq. 3)에서 $p^{\textrm{nf}}(x;\theta)=p_{T_{1},..,T_{n}}(x;\theta)$을 통해 $n$-layer flow model의 density를 얻을 수 있음:
    (Eq. 3) $p^{\textrm{nf}}(x;\theta)=p_{x_{0}}(T_{1},...T_{n}(x))\cdot | \det J_{T_{1},...,T_{n}}(x)|$
    - $\theta$ : 모든 layer에서의 transformation의 parameter

- Architecture Search for NF: Problem Definition

• 다양한 transformation으로 인해 optimal flow model을 구축하기 위한 design space는 상당히 큼
  • $n$-layer flow model의 경우, 각 layer는 각각 비용이 $\{C_{1},C_{2},..,C_{m}\}$인 $m$개의 transformation $\{T_{1},T_{2},...,T_{m}\}$ 중 하나를 기반으로 함
    - 결과적으로 search space에는 $m^{n}$개의 flow model이 포함됨
  • Architecture optimization의 목표는 $m^{n}$개의 flow model 중에서 최고의 performance-cost trade-off를 가지는 하나의 flow model을 찾는 것
    - 이때 performance는 target 분포 $p^{*}(x)$와 negative log-likelihood $p^{\textrm{nf}}(x;\theta)$ 간의 KL-divergence로 evaluate 됨
    - $p^{\textrm{nf}}(x;\theta)$의 cost는 모든 transformation layer cost의 합 $C^{\textrm{nf}}$
    - 결과적으로 performance-cost trade-off는 낮을수록 좋으므로, 이를 측정하기 위한 figure-of-merit (FOM)으로써 KL-divergence와 cost의 weighted sum을 사용함
  • 수학적으로, NF architecture search 문제는 모든 $n$-layer flow model에 대한 discrete optimization 문제로 볼 수 있음:
    (Eq. 4) $i^{*}=\arg \min_{i} D_{KL}\left[p^{*}(x)|| p^{\textrm{nf}}_{i}(x;\theta_{i}^{*})\right]+\lambda\cdot C^{\textrm{nf}}$
    $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \textrm{s.t.}\,\, \theta_{i}^{*}=\arg \min_{\theta_{i}} D_{KL}\left[ p^{*}(x)||p_{i}^{\textrm{nf}}(x;\theta_{i})\right]+\lambda\cdot C^{\textrm{nf}}$
    - $p_{i}^{\textrm{nf}}(x;\theta_{i})$ : $i$-th discrete $n$-layer flow model의 density function
    - $\lambda$ : performance-cost trade-off에 대한 user-defined factor, $i \in \{ 1,2,...,m^{n} \}$

3. Inapplicability of Existing D-NAS to NF Architecture Optimization

• (Eq. 4)의 조합 문제를 discrete optimization 하는 것은 어렵기 때문에 unconstructured neural network에 대한 differentiable NAS (D-NAS)를 고려해 볼 수 있음
  • D-NAS는 discrete optimization 문제를 discret solution constraint가 있는 continuous optimization 문제로 변환하고 이를 근사적으로 solve 함
  • 이때 D-NAS는 근사 조합 문제를 solve 하기 위해 2가지 mechanism을 활용
    1. Architecture parameter에 의해 weight 된 candidate neural network structure인 Supernet을 구축함
       - 이를 통해 discrete search space를 continuous space로 relax 하고, gradient-based optimization이 가능하도록 함
    2. Optimized continuous architectural solution에 대한 nearest binarization을 찾아 최종적인 optimal discrete architecture를 근사적으로 얻음
  • BUT, 기존 D-NAS에는 NF architecture optimization에 대한 inapplicability와 sub-optimality가 존재함
    1. Inapplicability
       - Supernet formulation은 optimization 중에 optimized NF model의 invertibility를 유지하지 않으므로 NF model에 대해서는 동작하지 않음
       - 두 invertible transformation의 weighted sum이 반드시 invertible 한 것이 아니기 때문
    2. Sub-optimality
       - Relaxed continuous optimal architectural solution을 찾을 수 있다고 가정하더라도,
       - D-NAS에서 discrete solution을 얻기 위해 binarizing한 final solution은 항상 optimal 하지 않을 수 있음
  • 따라서 AutoNF는 위 두 가지 문제를 해결하여, NF model에 대한 differentiable architecture optimization을 구축하는 것을 목표로 함
    1. 이를 위해 invertibility를 violating 하지 않는 새로운 mixture distribution formulation을 통해 search space에 대한 continuous relaxtion을 수행
    2. Binarization으로 인한 optimality 손실을 방지하기 위해, NP-hard 조합 최적화 문제를 unconstrained continuously relaxed 문제로 변환하여 solve 함
       

(좌) Mixture 분포에 대한 Superflow 구축 과정, (우) Binarized Flow Model의 Potential Sub-optimality

4. Methods

• 아래는 AutoNF의 continuous relaxtion이 기존의 discrete optimization 문제에 대해 globally optimal 하다는 것에 대한 증명 과정임

- Continuous Relaxtion by Mixture Distribution

• 먼저 $m$개의 optional transfromation $\{T^{1},T^{2},...,T^{m}\}$을 사용하여 $n$-layer flow model에서 $i$-th layer에 대한 continuous relaxtion을 유도한 다음, 해당 formulation을 모든 layer로 확장함
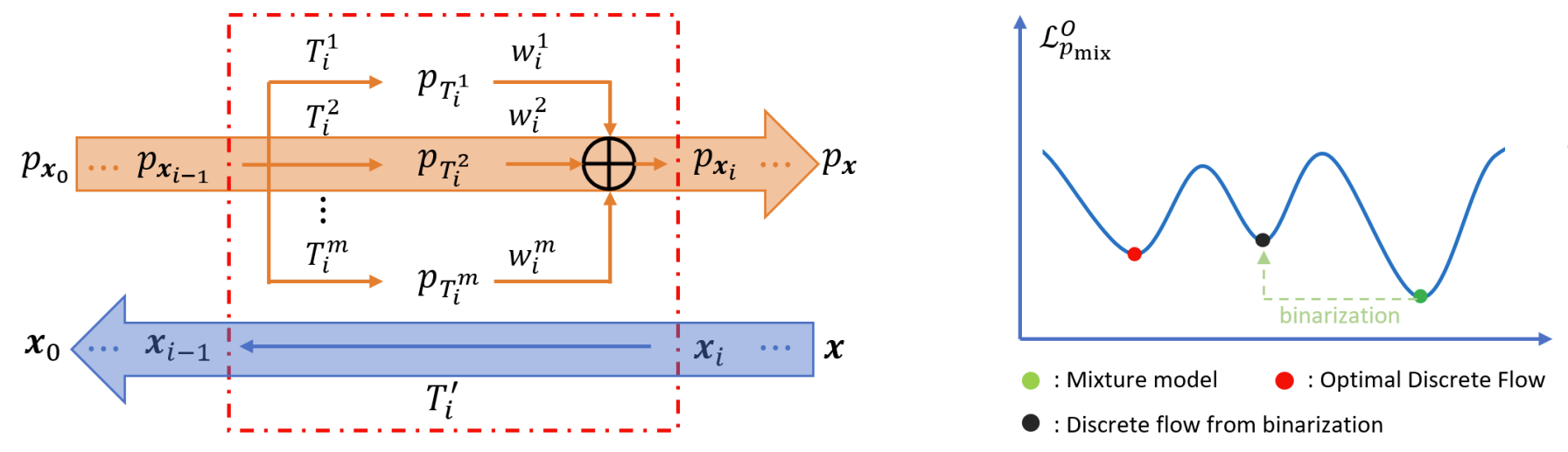
  • 이때 각 optional transformation $T^{j}$에 대해 architecture parameter $\alpha^{j}_{i}$를 도입하여 Softmax function에 의해 layer $i$로 select 될 확률을 모델링하면:
    (Eq. 5) $w_{i}^{j}=\frac{\exp(\alpha_{i}^{j})}{\sum_{j=1}^{m}\exp(\alpha_{i}^{j})}$
    - 이는 $T^{j}$의 weight로 볼 수 있음
  • NF에 대한 discrete architecture optimization 문제를 변환하는 continuous relaxtion을 위해, 모든 optional transformation을 고려하여 Superflow를 구축해야 함
    1. Continuous space에서 architecture parameter $\alpha$와 Superflow $\theta$의 model parameter 간의 joint optimization
    2. 이때 NF에 continuous relaxtion을 적용하는 것은 각 layer $i$에 대한 모든 candidate transformation의 weighted sum과 같음 : $T'_{i}=\sum_{j=1}^{m}w_{i}^{j}\cdot T^{j}$
    3. BUT, 여기서 $T'_{i}$는 항상 bijection이 아니므로, NF의 invertibility property가 위배됨
  • 따라서 AutoNF는 mixture distribution model로써 Superflow를 구축함
    1. $x_{i}$를 $x_{i-1}$ ($i \geq 1$)로 변환하기 위해, 각 $T^{j}$를 적용하여 새로운 density function $p_{T^{j}}(x_{i})$를 얻음:
       (Eq. 6) $p_{T^{j}}(x_{i})=p_{x_{i-1}}(T^{j}(x_{i}))\cdot | \det J_{T^{j}}(x_{i})|$
       
    2. 가능한 모든 $m$개의 density function은 $w^{j}_{i}$로 weighted sum 하여 desired mixture model $p_{x_{i}}(x_{i})$를 얻을 수 있음:
       (Eq. 7) $p_{x_{i}}(x_{i})=\sum_{j=1}^{m}w_{i}^{j}\cdot p_{T^{j}}(x_{i})\,\,\, \textrm{where} \,\, \sum_{j}^{m}w_{i}^{j}=1$
  • 이때 두 set의 random variable의 분포가 주어지면, random variable의 한 set를 다른 set로 mapping 하는 normalizing flow의 universal representation ability가 존재하는 것이 밝혀짐
    - 따라서, AutoNF의 mixture distribution도 마찬가지로 $p_{x_{i}}$를 $p_{x_{i-1}}$로 변환하는 $x_{i}$에서 $x_{i-1}$로의 implicit bijection $T'_{i}$가 존재하므로, mixture distribution은 NF의 invertibility를 만족함
• $n$-layer flow model에 대한 continuous relaxtion을 얻기 위해,
  • 각 layer에 mixture distribution formualtion을 recursive 하게 적용하여 $n$-layer model의 mixture distribution $p_{\textrm{mix}}(x;\theta,\alpha)$를 얻음:
    (Eq. 8) $p_{\textrm{mix}}(x;\theta,\alpha)=\sum_{j_{n}}^{m}w_{i}^{j_{n}}...\sum_{j_{1}}^{m}w_{i}^{j_{1}}\cdot [p_{T_{1}^{j_{1}}...T_{n}^{j_{n}}}(x;\theta) ]$
    - $i$-th layer의 $j$-th transformation과 weight를 각각 $T_{i}^{j_{i}}, w_{i}^{j_{i}}$로 나타냄
    - $p_{T_{1}^{j_{1}}...T_{n}^{j_{n}}}(x;\theta)$ : (Eq. 3)에 따라 정의되어 특정 $n$-layer flow model candidate의 density를 나타냄 
  • (Eq. 8)은 $m^{n}$개의 $n$-layer flow model candidate를 기반으로 하고, 각 candidate에는 $k=j_{1}+\sum_{i=2}^{n}(j_{i}-1)\cdot m^{i-1}$인 model index $k$가 할당됨
    1. 따라서 $k$-th $n$-layer flow model candidate의 density와 weight를 각각 $p_{k}(x;\theta_{k}), W_{k}$라 하고, (Eq. 8)을 rewrite:
       (Eq. 9) $p_{\textrm{mix}}(x;\theta,\alpha)=\sum_{k=1}^{m^{n}}W_{k}\cdot p_{k}(x;\theta_{k})$
       
    2. 유사하게 Superflow의 cost는 모든 discrete $n$-layer flow model cost의 weighted sum으로 정의됨:
       (Eq. 10) $C_{\textrm{mix}}(\alpha)=\sum_{k=1}^{m^{n}}W_{k}\cdot C_{p_{k}}$

• 모든 discrete $n$-layer flow model candidate의 density를 포함하는 feasible solution set를 $S$라고 하자
  • 그러면 NF에 대한 differentiable architecture optimization은 constrained optimization 문제 $OP_{1}$로 formulate 됨:
    (Eq. 11) $\arg \min_{\theta,\alpha}\mathcal{L}^{O}_{P_{\textrm{mix}}}(\theta,\alpha), \,\, \textrm{where} \,\, \mathcal{L}^{O}_{p_{\textrm{mix}}}(\theta,\alpha)= -\mathbb{E}_{p^{*}(x)}\left[\log (p_{\textrm{mix}}(x;\theta,\alpha)) \right]+\lambda\cdot C_{\textrm{mix}}(\alpha)$
    $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \textrm{s.t.}\,\, p_{\textrm{mix}}(x;\theta,\alpha)\in S$
  • 해당 $OP_{1}$을 original optimization이라 함

- Unconstrained Continuous Relaxtion of NF D-NAS Admitting Optimal Discrete Solution

• $OP_{1}$은 architecture optimization의 discrete nature로 인해 solve하기 어려운 mixture-binary programming 문제임
  • 따라서 기존 D-NAS와 같이 discrete NF model을 얻기 위해서 optimized continuous solution을 binarize 하면 sub-optimality가 발생함
  • 이때 $\mathcal{L}^{O}_{p_{\textrm{mix}}}$의 upper bound는 Jensen's inequality로 유도될 수 있음
    - 여기서 $\mathcal{L}^{U}_{p_{\textrm{mix}}}(\theta, \alpha)$의 unconstrained minimization은 $p_{z}(x;\theta_{z}^{*})$이 unique 하다는 mild condition 하에, 근사 binarization 없이 $OP_{1}$의 optimal discrete architectural solution $p_{z}(x;\theta_{z}^{*})$로 이어짐
    - 일반적으로 search space의 discrete flow model은 distinct 한 performance/cost를 가지므로 $p_{z}(x;\theta_{z}^{*})$의 uniqueness는 쉽게 충족됨
  • 따라서 이러한 unconstrained optimization 문제를 $OP_{2}$라고 함:
    (Eq. 12) $\arg \min_{\theta,\alpha} \mathcal{L}_{p_{\textrm{mix}}}^{U}(\theta, \alpha), \,\, \textrm{where} \,\, \mathcal{L}^{U}_{p_{\textrm{mix}}}(\theta, \alpha)=\sum_{k}^{m^{n}}W_{k}\cdot (-\mathbb{E}_{p^{*}(x)}[\log (p_{k}(x;\theta_{k}))])+\lambda\cdot C_{\textrm{mix}}(\alpha)$
• 이를 기반으로 $OP_{1}, OP_{2}$가 서로 equivalent 하고, 동일한 optimal discrete architectural solution $p_{z}(x;\theta_{z}^{*})$을 가짐을 증명
  • 편의 상, $\mathbb{E}$를 사용해 $\mathbb{E}_{p^{*}(x)}$를 대체하고 $M_{k}=-\mathbb{E}[\log(p_{k}(x;\theta_{k}))]+\lambda\cdot C_{p_{k}}$라 하자
  • [Proposition 1] Feasible solution set $S$의 모든 discrete flow model에 대해 $OP_{1}$과 $OP_{2}$의 loss는 동일하다.
    즉, $\forall p_{k}(x;\theta_{k})\in S, \, \mathcal{L}_{p_{\textrm{mix}}}^{O}=\mathcal{L}^{U}_{p_{\textrm{mix}}}$
  • [Proof]
    1. $S$의 임의의 $p_{k}(x;\theta_{k})$에 대해 $W_{k}=1$이고 $W_{i} = 0$이라고 가정했을 때,
    2. $i \neq k$라고 하면:
       (Eq. 13) $\mathcal{L}_{p_{\textrm{mix}}}^{O}(\theta_{k},\alpha_{k})=M_{k}=\mathcal{L}^{U}_{p_{\textrm{mix}}}(\theta_{k},\alpha_{k})$
  • [Therorem 1] $OP_{1}$의 optimal solution $p_{z}(x;\theta_{z}^{*})$가 unique 하면, $OP_{1}$과 $OP_{2}$는 equivalent 하고, 동일한 optimal solution $p_{z}(x;\theta_{z}^{*})$을 가진다.
  • [Proof]
    1. $\mathcal{L}^{U}_{p_{\textrm{mix}}}(\theta,\alpha)$는 (Eq. 10)의 cost model 정의를 기반으로, linear combination으로 나타낼 수 있다:
       (Eq. 14) $\mathcal{L}^{U}_{p_{\textrm{mix}}}(\theta,\alpha)=\sum_{k}^{m^{n}}W_{k}\cdot (-\mathbb{E}[\log(p_{k}(x;\theta_{k}))]+\lambda\cdot C_{p_{k}})$
    2. $k$-th flow candidate에 대해, $D_{KL}[p^{*}(x)||p_{k}(x;\theta_{k})]$을 $\theta_{k}^{*}$로써 최소화하는 optimal model parameter는 다음과 같이 나타낼 수 있다:
       (Eq. 15) $-\mathbb{E}[\log(p_{k}(x;\theta_{k}^{*}))]\leq -\mathbb{E}[\log(p_{k}(x;\theta_{k}))]$
    3. 그러면,
       (Eq. 16) $\mathcal{L}^{U}_{p_{\textrm{mix}}}(\theta,\alpha)=\sum_{k}^{m^{n}}W_{k}\cdot (-\mathbb{E}[\log(p_{k}(x;\theta_{k}))]+\lambda\cdot C_{p_{k}}) \geq \sum_{k}^{m^{n}}W_{k}\cdot(-\mathbb{E}[\log(p_{k}(x;\theta_{k}^{*}))]+\lambda\cdot C_{p_{k}})$
    4. 여기서 [Proposition 1]에 의해:
       (Eq. 17) $\mathcal{L}^{O}_{p_{\textrm{mix}}}(\theta^{*}_{k},\alpha_{k})=M^{*}_{k}=\mathcal{L}_{p_\textrm{mix}}^{U}(\theta_{k}^{*},\alpha_{k})$
    5. 정의에 따라, optimal discrete architectural solution $p_{z}(x;\theta_{z}^{*})$은 $M_{z}^{*}$로 표현되는 $OP_{1}$의 loss를 최소화하고, 이때 (Eq. 17)을 바탕으로 다음을 얻을 수 있다:
       (Eq. 18) $M_{z}^{*}=-\mathbb{E}[\log(p_{z}(x;\theta_{z}^{*}))]+\lambda\cdot C_{p_{z}} < -\mathbb{E}[\log(p_{k}(x;\theta_{k}^{*}))]+\lambda\cdot C_{p_{k}}=M_{k}^{*}$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \forall k\in\{1,2,...,m^{n}\}, \, k\neq z$
    6. (Eq. 15)와 (Eq. 18)을 결합하면:
       (Eq. 19) $\mathcal{L}^{U}_{p_{\textrm{mix}}}(\theta,\alpha)=\sum_{k}^{m^{n}}W_{k}\cdot (-\mathbb{E}[\log(p_{k}(x;\theta_{k}))] +\lambda \cdot C_{p_{k}})$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \geq \sum_{k}^{m^{n}}W_{k}\cdot(-\mathbb{E}[\log(p_{k}(x;\theta_{k}^{*}))]+\lambda\cdot C_{p_{k}})$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \geq \sum_{k}^{m^{n}}W_{k}\cdot(-\mathbb{E}[\log(p_{k}(x;\theta_{z}^{*}))]+\lambda\cdot C_{p_{z}})$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =-\mathbb{E}[\log(p_{z}(x;\theta_{z}^{*}))]+\lambda\cdot C_{p_{z}}$
    7. 따라서 (Eq. 19)는 $\mathcal{L}_{p_{\textrm{mix}}}^{U}(\theta,\alpha)$의 global minimizer가 $OP_{1}$의 optimal solution $p_{z}(x;\theta_{z}^{*})$임을 의미하고, $\theta=\theta_{z}$ 및 $W_{z}=1$인 경우 달성된다. $\blacksquare$

- Decomposed Search for Deep Flow Models

• Superflow는 $m^{n}$개 분포로 구성되므로, layer가 많은 deep architecture optimization은 computationally intensive 함
  • 계산 비용 문제를 해결하기 위해, 주어진 multiple-layer model을 각각 제한된 수의 layer를 포함하는 cascading block으로 decompose 함
  • 따라서 AutoNF는 unconstrained problem $OP_{2}$를 기반으로 해당 block을 한 번에 하나씩 sequentially optimize 함
    - 즉, 아래의 [Algorithm 1]과 같이 training data $X_{train}$과 validation data $X_{val}$에 대해
    - Model parameter $\theta$와 architecture parameter $\alpha$의 first-order bi-level optimization을 적용함

AutoNF Algorithm

5. Experiments

- Settings

• Dataset : UCI density estimation dataset (POWER, GAS, HEPMAS, MINIBOONE), BSDS300
• Comparisons : MAF, RQ-AF, RealNVP, RQ-C

- Results

• Performance-Cost Trade-offs of NF Models
  • AutoNF는 selected $\lambda$ 값을 고려하여 모든 dataset에 대해 더 나은 performance-cost trade-off를 갖춘 flow model을 찾을 수 있음
  • 기존 flow model 대비 최대 4.29배의 cost reduction 효과를 얻을 수 있음
  • 특히 MINIBOONE, BSDS300 dataset의 경우 AtuoNF가 가장 뛰어난 density estimation 결과를 보임

Performance-Cost Trade-off 비교

• Effect of Cost Term $\lambda$ on Architecture Search
  • 동일한 candidate transform에 대해 서로 다른 $\lambda$ 값으로 얻어진 flow model을 비교
    1. $\lambda$를 0으로 설정하면 AutoNF는 expressive flow를 찾는 것에만 집중하여, 높은 성능과 비용을 가진 flow model을 발견하는 것으로 나타남
    2. $\lambda$가 너무 크면 AutoNF는 비용이 가장 낮고 성능도 낮은 identity flow를 발견함
  • Pareto front는 $\lambda$를 tuning 함에 따라 AutoNF가 성능/비용을 서로 다르게 강조하는 flow model을 발견하고 더 나은 trade-off를 달성할 수 있음을 의미함

(좌, 중) 서로 다른 $\lambda$로 탐색된 Arhictecture의 Metric 비교, (우) 탐색된 Flow에서 파생된 Pareto Front

• The Benefit of Solving $OP_{2}$
  • Planar flow와 Radial flow를 포함하는 2가지 transformation option의 4-layer flow model을 탐색
    1. $M_{1}$ : binarization을 통해 $OP_{1}$을 solve / $M_{2}$ : $OP_{2}$를 directly solve
    2. $M_{2}$에 의해 optimize 되면, 각 layer의 transformation weight는 binary value로 수렴하고, binarization 없이도 discrete flow를 생성
    3. $M_{1}$의 경우, $OP_{1}$ loss에 대한 optimization이 mixture model로 이어지고, 이를 통해 nearest binarization으로 얻어진 $M_{1}$의 final flow는 $M_{2}$로 탐색된 flow 보다 낮은 성능을 보임
  • 결과적으로 $OP_{2}$를 solve 하면, 근사 binarization을 수행할 필요가 없고 AutoNF에 더 효과적임

$OP_{1}$과 $OP_{2}$의 비교