[Paper 리뷰] Transfer NAS with Meta-Learned Bayesian Surrogates

Transfer NAS with Meta-Learned Bayesian Surrogates

---

• Neural Architecture Search는 높은 계산 비용과 roubstness의 부족함에 대한 한계가 있음
• 특히 대부분의 방법론들은 prior knowledge를 무시하고 scratch로 최적의 architecture를 search 함
• TNAS
  • 다양한 dataset에 대한 prior architecture 평가를 통해 meta-learning 
  • Deep-kernel Gaussian process, Architecture embedding을 위한 graph neural network, Transformer-based encoder에 대해 Bayesian Optimization을 활용
• 논문 (ICLR 2023) : Paper Link

---

1. Introduction

• Neural Architecture Search (NAS)는 neural network에 대한 수동 설계 의존성을 줄이는 것을 목표로 함
  • BUT, 여전히 일반적으로 사용할 수 있는 강력하고 효율적인 NAS 방법론은 아직 없음
    - Reinforcement Learning, Bayesian Optimization과 같은 blackbox 최적화는 안정적으로 동작하지만 느림
    - One-shot NAS의 경우 빠르지만 robustness에 문제가 있음
    - Zero-cost Proxy는 architecture 성능에 대한 information을 제공해주지 못함
  • NAS에서 dataset 간의 transfer information에 대한 연구도 여전히 부족함
    - NAS에서 transfer learning은 새로운 task를 위해 prior knowledge와 앞서 설계된 architecture를 재사용 가능하게 함
  • BUT, information transfer를 적용한 이전의 NAS 방법론들은 몇 가지 한계가 있음
    1. 방대한 data에서 활용하기에는 어려움
    2. Search space가 제한적이고, pre-selected architecture에서만 선택하는 경향을 보임
    3. Test data와 같은 unseen data에 제대로 적응하지 못함
  • 추가적으로 NAS의 효율성을 높이기 위해 Hyper Parameter Optimization (HPO) 문제로 접근할 수 있음

-> 그래서 one-shot NAS 수준의 계산 비용과 blackbox 최적화의 reliability를 모두 만족하는 새로운 NAS 방법론인 TNAS를 제안

 

• TNAS
  • Deep-kernel surrogate를 사용한 효율적인 Bayesian Optimization (BO) 기반 NAS 방법론
  • BO에 대한 transfer learning 위해 dataset-contextualized surrogate를 도입
    - Graph encoder를 사용하여 neural architecture를 encoding
    - Dataset encoder를 사용하여 context feature를 얻음
    - Deep kernel learning을 활용하여 architecture와 dataset의 joint space에 대한 meta-learning kernel을 얻은 다음 효율적인 BO를 수행
  • 위 approach의 장점:
    - Exploration/Exploitation의 trade-off를 만족
    - Test task에 대해 meta-learning으로 관찰된 내용을 맹목적으로 따라 하는 것을 방지

< Overall of TNAS >

• NAS를 few-shot learning 문제로 취급하여 transfer HPO의 Bayesian Optimization kernel을 meta-learning
• Deep-kernel Gaussian Process를 graph neural network, transformer-based dataset encoder와 결합
• 결과적으로 다른 blackbox NAS, one-shot NAS 방법론들보다 우수한 성능을 달성

2. Proposed Method

• TNAS는 아래의 문제를 고려:
  • $Q$개 dataset에 대한 history가 주어지면 각 dataset $\mathcal{D}^{(q)}$에 대해,
    - Neural network architecture $x_{1}^{(q)}, ..., x_{n}^{(q)}$를 연관된 성능 $y_{1}^{(q)}, ..., y_{n}^{(q)}$ (accuracy 등)으로 미리 평가하고,
    - 새로운 dataset $\mathcal{D}^{(new)}$에서 dataset의 history를 활용하여 최적의 architecture를 빠르게 search 하는 것을 목표로 함
  • 이를 해결하기 위해 few-shot Bayesian Optimization (BO)를 활용
    - Dataset 전반에 걸쳐 hyperparameter configuration을 transferring
    - 이때 deep-kernel learning은 일반적인 BO 설정에서 Gaussian Process (GP) surrogate로 사용됨
• Hyperparameter configuration은 일반적으로 $N$차원 vector로 표현될 수 있지만, neural network architecture는 표현하기 어려움
  • 단순히 architecture를 vector로 표현하고 이를 GP kernel에 연결하는 것은 부적합할 수 있음
    - 실제로 architecture representation이 NAS 성능에 큰 영향을 미침
  • 이를 위해 Graph Neural Network (GNN)을 사용하여 neural network에 대한 learnable representation을 얻음
    - GNN은 architecture를 자연스럽게 graph로 표현하기 때문에 NAS에서 효과적임
• Architecture encoding을 GP kernel에 직접 제공할 수 있지만, architecture 간의 similarity를 평가하려면 kernel이 dataset의 특성에 따라 condition 되어야 함 
  • 이때 유사한 sub-graph component (GNN encoding)을 공유하고, target dataset에 대해 유사한 성능을 달성할 때, 두 architecture는 유사하다고 볼 수 있음
  • 따라서, dataset의 특성 (meta-feature)에 따라 deep kernel을 condition 함
    1. Set transformer를 사용하여 dataset의 learnable representation을 사용하고,
    2. Architecture와 dataset encoding을 fully-connected neural network로 처리하고,
    3. 해당 output을 Matern kernel과 같은 off-the-shelf kernel의 input으로 사용하여 architecture, dataset에 대한 datapoint의 거리를 계산
  • 결과적으로 end-to-end learnable encoding이 생성되고 GNN, transformer, fully-connected neural network의 parameter는 meta-learning 됨

Overall of TNAS

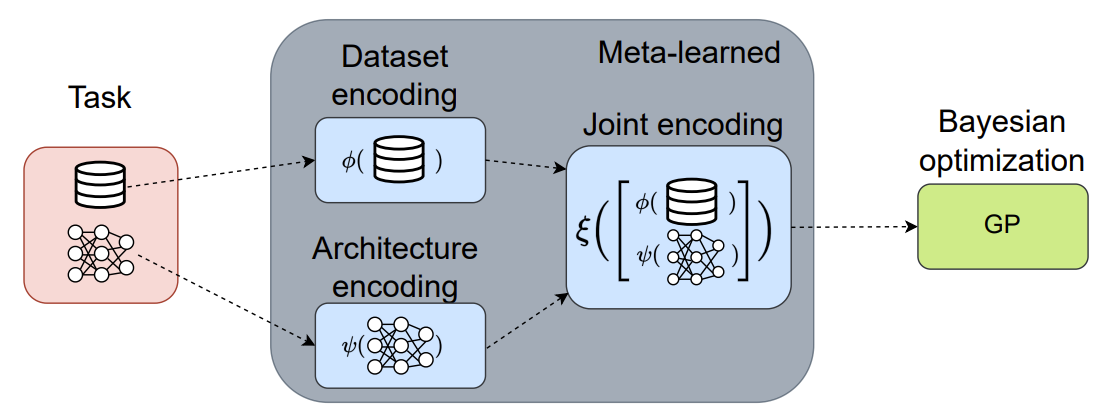
- Bayesian Optimization with Deep Kernel Gaussian Process

• Bayesian Optimization (BO) 내에서 Gaussian Process (GP) surrogate를 정의
  • Input $x \in \mathcal{X}$는 hyperparameter configuration을 나타내고, target $y \in \mathcal{Y}$은 hyperparameter configuration $x$로 학습했을 때의 성능을 의미
  • Training $\mathcal{D} = \{ (x_{i}, y_{i}) \}_{i=1}^{n}$와 Testing $\mathcal{D}^{*} = \{ (x_{i}^{*}, y_{i}^{*} ) \}_{i=1}^{n^{*}}$에 대한 dataset split이 있을 때,
    - GP는 function에 대한 prior를 가정하고 feature $x \in \mathcal{X} \subseteq \mathbb{R}^{L}$이 주어졌을 때, target $y \in \mathcal{Y} \subseteq \mathbb{R}_{+}$을 근사하는 non-parametric model
    - 이때, test instance $x^{*}$에 대한 target variable의 추정 $y^{*}$는 jointly Gaussian으로써:
    $ \left [ \begin{matrix} y \\ y^{*} \end{matrix} \right ] \sim \mathcal{N} \left( 0, \begin{pmatrix}
     K(x,x) & K(x,x^{*}) \\
     K(x,x^{*})^{T} & K(x^{*}, x^{*})  \\
    \end{pmatrix}\right)$
    - 공분산 행렬의 각 block은 instance pair에 kernel function $k : \mathcal{X} \times \mathcal{X} \rightarrow \mathbb{R}_{+}$을 적용한 것 ($K(x,x^{*})_{i,j} := k(x_{i}, x_{j}^{*})$)
  • 이때 test instance $x^{*}$의 target $y^{*}$에 대한 GP의 추정된 posterior 평균과 공분산은:
    (Eq. 1) $\mathbb{E}[y^{*} | x^{*}, x, y] = K(x^{*}, x)K(x,x)^{-1}y$
    (Eq. 2) $cov[y^{*}|x^{*},x] = K(x^{*},x^{*})-K(x,x^{*})^{T}K(x,x)^{-1}K(x,x^{*})$
    
  • GP는 Matern kernel과 같은 kernel function $k$를 통해 얻어지는 training instance에 대한 test instance의 similarity에 의존하는 lazy model
    - 이때 일반적인 kernel은 sub-optimal 가정으로 인해 GP의 성능을 저하시킬 수 있음
  • 따라서 강력하고 효율적인 kernel function을 사용하기 위해 Deep Kernel Learning을 도입
    - Deep Kernel Learning은 kernel을 trainable neural network로 표현
    - Mapping $\xi : \mathcal{X} \rightarrow \mathbb{R}^{L}$은 유사한 instance가 co-loacte 되어 있는 latent representation으로 feature를 projection 함
• The Embedding $\xi$ for the Deep Kernel
  • Embedding $\xi$는 fully-connected neural network
    - Architecture encoding $\psi$와 Dataset encoding $\phi$를 input으로 사용
  • 구체적으로,
    1. $L$차원 architecture encoding $\psi$는 $K$차원 dataset encoding $\phi$과 fuse 되고,
    2. Fully-connected neural network $\xi: \mathbb{R}^{K+L} \rightarrow \mathbb{R}^{M}$을 통해 처리됨
       - 이때 마지막 layer는 $M$개의 neuron을 가짐
  • 여기서 사용될 input을 구성하기 위해 TNAS는 GNN-based architecture encoding과 transformer-based dataset encoding을 활용
• The Architecture Encoding $\psi$
  • Architecture encoding $\psi$를 얻기 위해 Directed Acyclic Graph (DAG) encoder를 사용
    1. GRU cell 하나를 사용하여 input에서 output 방향으로 topological order를 traverse 하고,
       
    2. 다른 GRU cell을 사용하여 DAG를 backward direction으로 pass 함으로써 graph의 latent representation을 얻음
    3. 최종적으로 fully-connected layer를 통해 architecture encoding을 얻음
• The Dataset Encoding $\phi$
  • Dataset encoding $\phi$는 2개의 stacked Set-Transformer architecture로 구성됨
    1. 첫 번째 Set-Transformer layer는 동일한 class의 무작위로 sampling 된 datapoint 간의 interaction을 capture
    2. 두 번째 Set-Transformer layer는 서로 다른 class의 interaction을 capture
    3. 최종적으로 두번째 Set-Transformer의 output으로써 dataset encoding을 얻음
  • 추가적으로 TNAS는 meta-training dataset에 대한 multi-fidelity Bayesian Optimization method (BOHB)를 사용하여 dataset encoder와 graph encoder의 embedding 차원을 조정
• Putting it all together
  • Dataset $\mathcal{D}$에서 평가된 $x$와 dataset $\mathcal{D}^{'}$에서 평가된 $x^{'}$ 간의 architecture kernel/similarity는:
    $k(x, \mathcal{D}, x^{'},\mathcal{D}^{'}; w) = k \left( \xi([ \psi(x;w^{(\psi)}),\phi(\mathcal{D};w^{(\phi)})];w^{(\xi)}), \xi([\psi(x^{'};w^{(\psi)}), \phi(\mathcal{D}^{'};w^{(\phi)})];w^{(\xi)});w^{(k)} 
    \right)$
    - $w^{(\xi)}$ : neural network $\xi$의 parameter
    - $w^{(\psi)}$ : $\psi$를 encoding 하는 architecture의 parameter
    - $w^{(\phi)}$ : $\phi$를 encoding하는 dataset의 parameter
    - $w^{(k)}$ : kernel function의 additional parameter
  • 이때 cumulative parameter를 $w := (w^{(\xi)}, w^{(\psi)}, w^{(\phi)}, w^{(k)})$로 나타낼 수 있고, 모든 parameter는 marginal likelihood를 최대화함으로써 meta-learning 됨

- Meta-Learning Deep-Kernel GP Surrogates

• $Q$개의 dataset이 주어졌을 때, 각 dataset $\mathcal{D}_{q}$는 $N_{q} \in \mathbb{N}_{+}$의 평가된 architecture가 존재함
  • $q$-th dataset에서 평가된 $n$-th architecture를 $x_{q,n}$이라고 하고, 해당하는 validation accuracy를 $y_{q,n}$이라고 하자
  • 이때, 모든 dataset에 대한 모든 evaluation의 meta-dataset은: 
    $\mathcal{M} := \cup_{q=1}^{Q} \cup_{n=1}^{N_{q}} \{ (x_{q,n},y_{q,n},\mathcal{D}_{q} )\}$
    - $x := (x_{1,1}, ..., x_{Q, N_{q}}), y := (y_{1,1}, ..., y_{Q, N_{q}}), D := (D_{1}, ..., D_{Q})$ : 각각 모든 arhictecture, accuracy, dataset에 대한 vector
  • Deep kernel의 parameter $w$는 meta-training dataset에서 GP surrogate의 log marginal likelihood를 최대화함으로써 jointly optimize 됨:
    (Eq. 3) $\underset{w}{argmax} \,\, log \, p(y | x, \mathcal{D};w) \propto \underset{w}{argmin} \,\, y^{T}K^{-1}(x,\mathcal{D};w)y + log \, |K(x,\mathcal{D};w)|$
• 이때 학습은 mini-batch sampling과 stochastic gradient descent (SGD)를 활용하여 수행됨
  • 모든 component가 differentiable 하므로 결과적으로 end-to-end differentiable 함
  • Meta-parameter $w$를 업데이트하기 위해, REPTILE meta-learning algorithm을 활용
    
    1. Validation accuracy를 사용하여 (architecture, dataset) pair에 대한 mini-batch를 sampling|
       - 이때 meta-training dataset에서 uniform sampling
    2. (Eq. 3)에 대해 SGD를 적용하여 dataset $\mathcal{D}$에서 architecture $x$의 accuracy $y$를 추정하는 surrogate를 적합
    3. 최종적으로 REPTILLE을 사용하여 $w$를 업데이트

Deep-kernel GP에 대한 Meta-learning algorithm

- Meta-Testing

• 최적의 $w$를 찾으면 GP에 대한 meta-learned kernel을 posterior에 연결
  • 이후 vanilla Bayesian Optimization (BO)을 사용하여 새로운 response surface에서 최적의 configuration을 식별
  • Meta-test에서 BO를 사용함으로써 TNAS는 GP surrogate의 posterior를 test task에 대한 function evaluation으로 업데이트하여 test task에 적응할 수 있음 (by Eq.1, Eq.2)

3. Experiments

- Settings

• Search Spaces : NAS-Bench-201, MobileNet V3
• Datasets : CIFAR-10, CIFAR-100, SVHN, Aircraft, Oxford IIT Pets, MNIST
• Comparisons
  - Classic HPO : Random Search (RS), Expected Improvement (EI), Upper Confidence Bound (UCB), HEBO
  - HPO for NAS : BANANAS, NASBOWL
  - SOTA in NAS : GDAS, SETN, PC-DARTS, DrNAS
  - Transfer NAS : MetaD2A

- Research Hypothesis and Experimental Results

• TNAS를 검증하기 위해 3가지 가설을 설정
  1. Hypothesis 1 : TNAS는 classic HPO 및 NAS에 적용된 HPO 방법론들보다 더 효율적이고 우수한 성능을 달성할 것이다
  2. Hypothesis 2 : TNAS는 runtime 측면에서 one-shot approach보다 경쟁력 있을 것이다
  3. Hypothesis 3 : TNAS는 one-shot 방법론들만큼 효율적이면서 HPO와 같은 blackbox 최적화의 consistency를 달성할 것이다
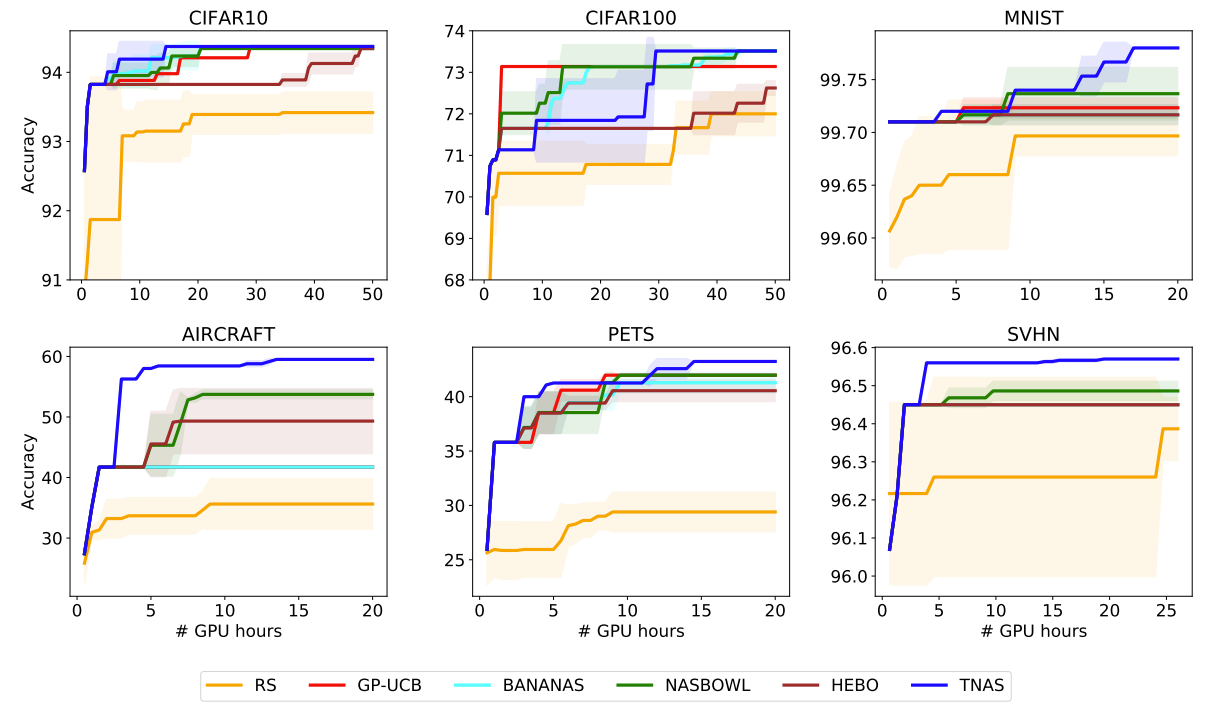
• Result for Hypothesis 1
  • TNAS의 성능을 다른 HPO들과 비교해 보면, CIFAR-100을 제외한 모든 dataset에서 TNAS는 더 빠르고 우수한 성능의 architecture를 search 함
  • 추가적으로 모든 benchmark에 대해서도, TNAS가 가장 좋은 성능을 발휘

TNAS와 HPO들 간의 성능 비교

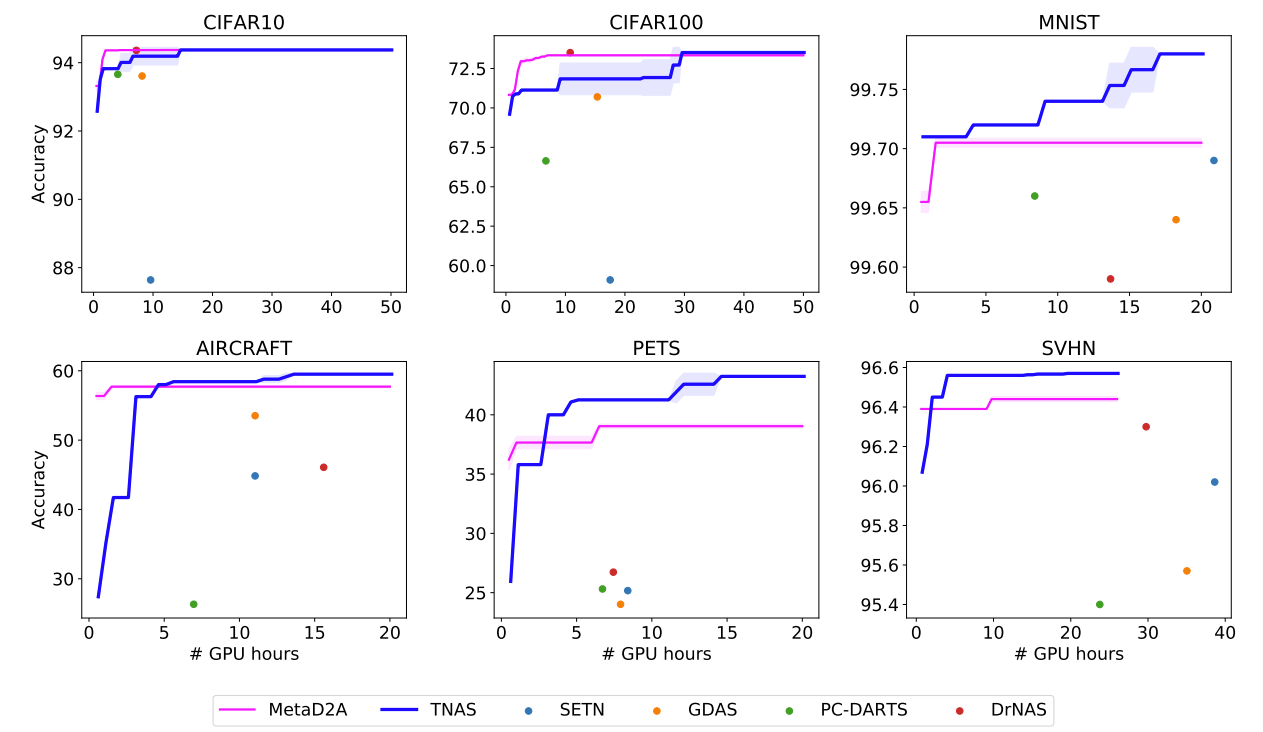
• Results for Hypothesis 2
  • TNAS는 Bayesian Optimization 내에서 meta-learned deep kernel을 사용하여 search time을 one-shot approach와 비슷한 수준으로 줄일 수 있음
  • 결과적으로 CIFAR-10, CIFAR-100을 제외하고 TNAS는 one-shot 방법론들의 search time보다 빠름
  • 특히 비슷한 transfer NAS 방법론인 MetaD2A와 비교해보면
    - MetaD2A는 exploration/exploitation의 trade-off를 무시하고 meta-training 과정에서 관찰된 것만 활용
    - MetaD2A는 새로운 target dataset에 대한 feedback을 활용하지 않아 다양한 dataset에서 stagnate를 보임

TNAS와 다른 NAS 방법론들 간의 비교

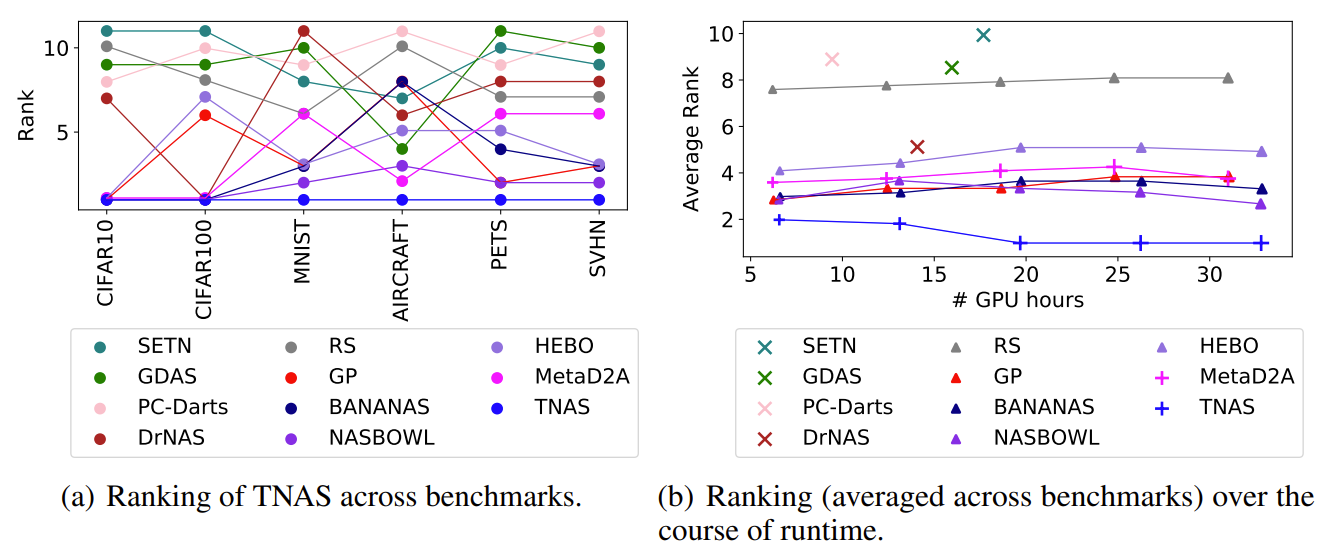
• Results for Hypothesis 3
  • TNAS는 지속적으로 우수한 성능을 달성하는 반면, 다른 NAS 방법론들은 benchmark 전체에 대해 순위가 계속 변화함
  • TNAS는 대/소규모의 computational budget에서 꾸준히 최고 성능을 달성함

TNAS의 consistency 비교

- Ablating Our Design Choices

• TNAS에서 도입된 graph와 dataset encoder와 같은 design choice를 분석
  - 결과적으로 해당 design들을 사용하지 않았을 때 보다, learnable dataset meta-feature와 graph neural network를 모두 사용했을 때, TNAS는 가장 우수한 성능을 보임

Ablation Study 결과

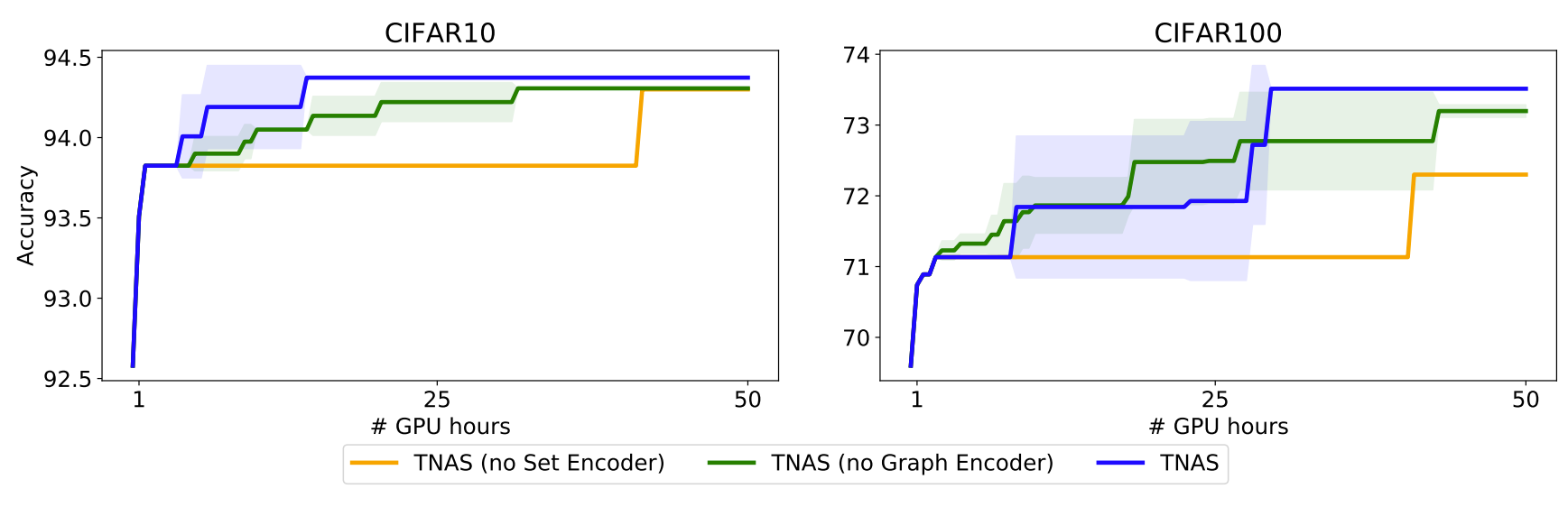
• Meta-learning의 효과와 다양한 initial architecture에 대한 성능을 확인해 보면, 두 design choice가 모두 TNAS의 성능 향상에 효과적임을 알 수 있음

Meta Learning과 Initialization의 효과