[Paper 리뷰] LSPNet: An Ultra-Low Bitrate Hybrid Neural Codec

LSPNet: An Ultra-Low Bitrate Hybrid Neural Codec

---

• Ultra-low bitrate에서도 동작할 수 있는 neural codec이 필요함
• LSPNet
  • LPCNet framework를 기반으로 parameteric encoder를 combine 하여 Line Spectral Pair를 incorporate
  • 추가적으로 STFT loss와 Cross-Entropy loss를 활용한 Joint Time-Frequency training strategy를 적용
• 논문 (INTERSPEECH 2025) : Paper Link

---

1. Introduction

• 1.2kbps의 ultra-low bitrate speech coding에서 intelligible, natural-sounding speech를 얻기 어려움
  • 특히 Mixed-Excitation Linear Prediction (MELP), Code-Excited Linear Prediction (CELP)와 같은 기존 speech codec은 low bitrate에서 robotic speech나 muffed artifact가 발생함
  • 한편으로 Deep Neural Network (DNN)-based speech coding을 활용하면 더 나은 품질을 달성할 수 있음
    1. 대표적으로 LPCNet은 parametric codec과 neural vocoder를 combine 하여 low computational footprint와 high speech quality를 달성함
       - BUT, Lienar Predictive Coding (LPC) coefficient가 quantization error에 sensitive 하다는 한계점이 있음
    2. SoundStream, EnCodec, DAC의 경우 fully end-to-end neural network를 활용하여 explicit parametric feature extraction에 대한 의존성을 줄임
       - BUT, 해당 방식은 Transformer, diffusion structure 등으로 인해 상당한 complexity가 존재함

-> 그래서 low computational cost의 ultra-low bitrate speech codec인 LSPNet을 제안

 

• LSPNet
  • Bark Frequency Cepstral Coefficient (BFCC) 보다 numerical stability, quantization error tolerance가 더 높은 Linear Spectral Pair (LSP)를 사용하여 spectral envelope를 convey
  • LPCNet의 explicit linear prediction estimation stage를 direct audio sample prediction으로 replace
  • Speech quality 향상을 위해 STFT-based loss와 Cross-Entropy loss를 도입
  • 추가적으로 complexity를 줄이기 위해 parametric encoder를 활용하여 speech feature를 추출

< Overall of LSPNet >

• LPCNet을 기반으로 LSP와 parametric encoder를 적용한 ultra-low speech codec
• 결과적으로 기존보다 우수한 성능을 달성

2. Method

• LSPNet은 LPCNet을 기반으로 hybrid approach를 채택함
  • LSPNet은 Codec2의 low-complexity encoder part를 활용하여 encoded audio를 represent 하는 feature를 추출하고, 이를 quantize 한 다음, compact bitstream으로 encode 함
  • 이후 dequantized bitstream을 feature vector로 neural decoder를 training 하여 reconstructed speech quality를 향상함

- Parametric Encoder

• Encoder는 information을 effectively compress 하면서 reconstruction에 필요한 essential feature를 추출함
  • 이를 위해 SoundStream, HiFi-Codec과 같이 data-driven manner로 transmission parameter를 학습하는 neural network를 고려할 수 있지만, high computational resource가 요구됨
    
  • 따라서 논문은 parametric encoder를 채택하여 spectral envelope, pitch, voicing level을 explicitly modeling 함
    1. 특히 1.2kpbs mode의 Codec2 sinusoidal coder는 8kHz의 sample rate로 40ms frame에서 동작함
       - 이때 encoder는 10-th order LSP, energy, pitch, voiced/unvoiced flag를 추출함
    2. 결과적으로 해당 parameter는 bitstream으로 compress 되고, 각 40ms frame은 48bit로 encoding 됨
    3. LSP는 multi-stage Vector Quantization (VQ)를 사용하고, singal energy와 pitch에는 joint VQ가 사용됨

Overview

- Neural Decoder

• LSPNet을 training 하는데 필요한 input feature는 dequantized Codec2 bitstream에서 추출됨
  • LPCNet은 Bark scale에서 compute 된 18-cepstral coefficient를 사용하는 반면, 논문은 spectral envelope information에 대한 10-th ordere LSP에 의존함
  • 구조적으로 LSPNet은 LPCNet의 frame-by-frame, sample rate module을 inherit 함
    1. Frame-level에서 input frame은 2개의 convolutional layer와 2개의 dense layer를 통해 처리됨
       - 해당 network는 latent frame-level feature를 추출하여 audio signal에서 temporal dimension과 high-level pattern을 capture 함
    2. Sample-level에서는 frame-level에서 추출된 latent feature가 2개의 GRU layer, dual dense layer로 전달됨
       - Dual dense layer는 individual audio sample의 probability distribution을 predict 함
  • 특히 논문은 LPCNet과 달리 16-bit linear PCM으로 convert 하기 전에 $\mu$-law domain에서 sample value를 predict 함
    - 해당 direct prediction approach는 training objective를 simplify 하고, intermediate LPC computation을 eliminate 하여 streamlined approach를 지원함

- Loss Function

• LSPNet은 frame-level STFT loss component를 balance 하여 weighted loss를 minimize 하도록 training 됨
  • 이때 기존 LPCNet의 sample-wise Cross-Entropy (CE) loss도 추가적으로 사용됨
  • STFT Loss
    1. STFT loss는 input frame $s$에서 model output $s'=\text{LSPNet}\{\text{Codec2_enc}(s)\}$를 frequency domain의 ground-truth input과 compare 함
    2. 즉, generated spectral response $S'=\text{FFT}(s')$을 Hamming windowed $w$ input spectral response $S=\text{FFT}(s\times w)$와 compare 함:
       (Eq. 1) $\mathcal{L}_{S}=\sum_{t,f}\left[\left(|S_{t,f}|-|S'_{t,f}|\right)^{2}+0.1\left| \angle S_{t,f}-\angle S'_{t,f}\right|\right]$
  • CE Loss
    1. 해당 loss는 time domain에서 $N$ sample과 $J$ class에 대해, predicted $s'$과 ground-truth $s$ sample distribution 간의 sparse categorical CE loss를 optimize 함:
       (Eq. 2) $ \mathcal{L}_{CE}-\sum_{n=1}^{N}\log\left(e^{s_{n}}/\sum_{j=1}^{J}e^{s'_{j}}\right)$
  • 결과적으로 total loss $\mathcal{L}_{tot}$는 factor $\alpha$를 통해 time, spectral component를 balance 함:
    (Eq. 3) $\mathcal{L}_{tot}=\alpha \mathcal{L}_{S}+(1-\alpha)\mathcal{L}_{CE}$

- Training Strategy

• Model robustness와 performance를 향상하기 위해 논문은 pseudo-batch training을 채택함
  • Training 시 각 batch 내의 frame은 randomly shuffle 되어 frame type의 diversity를 보장함
  • 추가적으로 noise resilience와 generalization을 개선하기 위해 audio의 $\mu$-law domain에 discrete uniform distributed random noise를 도입함
    - 해당 augmentation은 model의 real-world adaptation을 지원하여 다양한 scenario에서의 reliability를 향상함

3. Experiments

- Settings

• Dataset : LibriTTS
• Comparisons : LPCNet, EnCodec, DAC, Opus, Codec2

- Results

• 전체적으로 LSPNet이 가장 우수한 성능을 달성함

Model 성능 비교

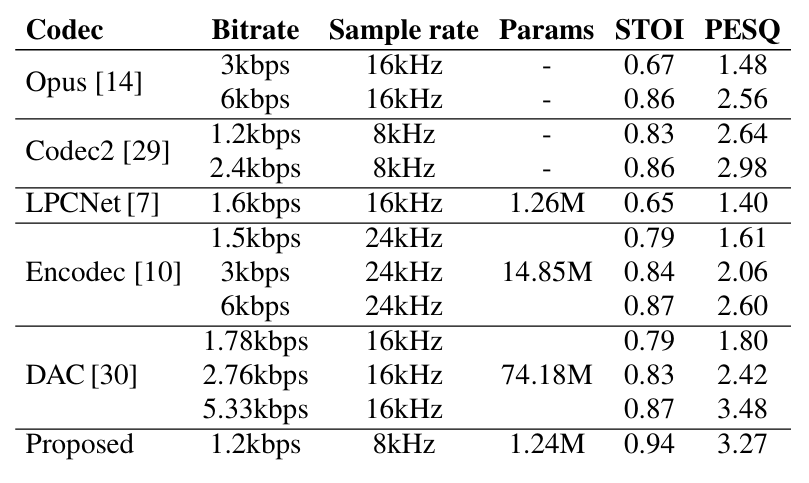
• Box plot 측면에서도 LSPNet이 가장 우수함

Box Plot

• LSPNet은 가장 높은 선호도를 보임

선호도 비교

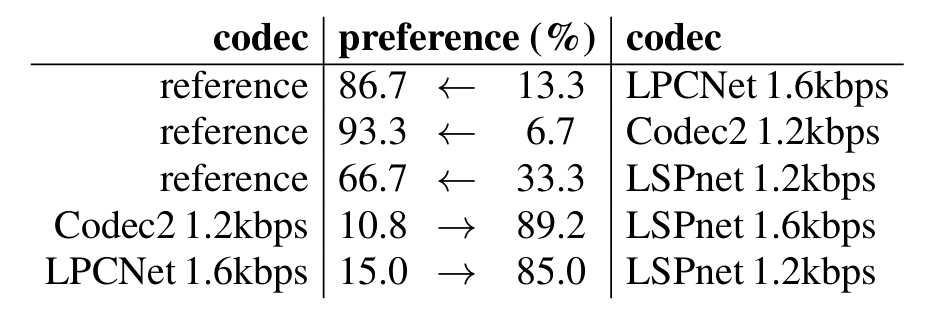
• Optimal Loss Weighting
  • Loss weight $\alpha=0.5$로 설정하면 최적의 성능을 달성할 수 있음

Loss Weight 별 성능