[Paper 리뷰] Recycle-and-Distill: Universal Compression Strategy for Transformer-based Speech SSL Models with Attention Map Reusing and Masking Distillation

Recycle-and-Distill: Universal Compression Strategy for Transformer-based Speech SSL Models with Attention Map Reusing and Masking Distillation

---

• HuBERT와 같은 Speech Self-Supervised Learning model은 상당한 parameter 수를 가짐
• ARMHuBERT
  • Transformer layer에 대해 attention map을 reuse 하여 model을 compress
  • Student model의 representation quality를 향상하기 위해 masking distillation strategy를 도입
• 논문 (INTERSPEECH 2023) : Paper Link

---

1. Introduction

• Wav2Vec 2.0, HuBERT, WavLM과 같은 Transformer-based Self-Supervised Learning (SSL) model은 다양한 speech downstream task에서 우수한 성능을 달성함
  • BUT, 해당 model은 parameter 수가 많고 training time이 길어 resource-limited 환경에서 활용하기 어려움
    - 따라서 SSL model은 parameter-efficient training과 lower computational overhead를 보장해야 함
  • 한편으로 SSL model compression을 위해 LightHuBERT, DistilHuBERT, FitHuBERT 등을 고려할 수 있지만, 다음의 한계점을 가짐:
    1. Wide-and-Shallow student model은 content-related downstream task에서 성능 저하를 보임
    2. Layer-to-Layer (L2L) distillation은 모든 layer parameter가 필요하므로 counter-intuitive 함
    3. Architecture pruning은 resource-limited 환경에서 training 하기 어려움

-> 그래서 효과적인 SSL model compression을 위해 Recylce-and-Distill strategy를 제안

 

• ARMHuBERT
  • Student Transformer layer에 대해 attention map을 reusing
    - 이를 통해 특정 Transformer layer의 key, query parameter를 remove 할 수 있으므로, L2L distillation과 같이 모든 layer parameter를 retain 할 필요가 없음
  • 추가적으로 better speech representation quality를 위해 masking strategy를 도입

< Overall of ARMHuBERT >

• Attention map reusing과 masking strategy를 적용한 compressed SSL model
• 결과적으로 기존보다 우수한 성능을 달성

2. Method

- Attention Map Reusing

• Attention map reusing은 pre-trained Transformer model 내에서 head, layer 간의 attention map similarity를 활용하여 student model을 compress 함
  • Transformer의 Multi-Head Self-Attention (MHSA) module에서 input $x\in \mathbb{R}^{n\times d}$는 transformation matrix $W_{h,k},W_{h,q}\in\mathbb{R}^{d\times d_{k}}$와 $W_{h,v}\in\mathbb{R}^{d\times d_{v}}$를 사용하여 $H$ independent query로 transform 됨:
    (Eq. 1) $ K_{h}=W_{h,k}x,\,\,\,K_{h}\in\mathbb{R}^{n\times d_{k}},$
    $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,Q_{h}=W_{h,q}x,\,\,\,Q_{h}\in\mathbb{R}^{n\times d_{k}},$
    $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,V_{h}=W_{h,v}x,\,\,\,V_{h}\in\mathbb{R}^{n\times d_{v}}$
    - $h$ : head, $n$ : sequence length
    - $d_{k},d_{v},d$ : key, value, model의 width
  • 이후 key, query는 width-axis를 따라 multiply 되어 scaled dot-product attention map $A_{h}\in\mathbb{R}^{n\times n}$을 얻고, 각 head에 대한 attention map과 value의 linear combination을 concatenate 하여 original width로 project 됨:
    (Eq. 2) $A_{h}=\text{softmax}\left(Q_{h}K_{h}^{\top}/\sqrt{d_{k}}\right)$
    (Eq. 3) $\text{MHSA}(x)=\left[A_{1}V_{1},...,A_{H}V_{H}\right]W_{o},\,\,\, W_{o}\in\mathbb{R}^{Hd_{v}\times d}$
  • Attention map reusing은 $A_{h}$를 previous layer의 attention map으로 replace 하는 것과 같음
    1. Current layer $\ell$에서 $k$-th previous attention map을 reuse 했을 때, ReusedMHSA module은:
       (Eq. 4) $\text{ReuseMHSA}(x)=\left[A_{1}^{\ell-k}V_{1}^{\ell},...,A_{H}^{\ell-k}V_{H}^{\ell}\right] W_{o}^{\ell}$
    2. 여기서 $K_{h},Q_{h}$ computing을 ommit 할 수 있으므로, multiplication과 addition 수는 $(2nd^{2}+n^{2}d)$로 reduce 됨
       - $d/H=d_{v}=d_{k}$라고 가정하면, ommited computation은 original MHSA computation $(4nd^{2}+2n^{2}d)$의 절반에 해당함
    3. 결과적으로 더 많은 ReuseMHSA module을 사용할수록 parameter와 Multiply-Accumulated (MAC)이 줄어듦

Overview

- Masking Distillation

• Attention map reusing은 student model의 representation quality에 영향을 줄 수 있음
  • 따라서 student representation learning을 향상하기 위해 논문은 masking distillation scheme을 도입함
  • Speech frame masking에서 model은 other unmasked frame을 기반으로 masked frame을 accurately represent 하도록 training 됨
    
    1. 여기서 teacher model은 masked frame의 representation을 guide 함
    2. $\mu(x)$를 masked input, $f^{t},f^{s}$를 각각 teacher, student model이라 했을 때 masked loss는:
       (Eq. 5) $\mathcal{L}(x)=\frac{1}{|M|}\sum_{i\in M}\left|\left| f_{i}^{t}(x)-f_{i}^{s}(\mu(x))\right|\right|_{2}$
       - $f_{i}$ : speech representation의 $i$-th frame, $M$ : masked frame set
  • (Eq. 5)의 masked part loss 외에도 teacher model이 unmasked frame에서 high-quality representation을 provide 하도록 unmasked loss를 추가적으로 도입함
    1. 이때 masking process가 essential frame을 remove 하는 경우, $f^{t}(x)$의 intact form을 distill 했을 때 remove 해야 할 essential knowledge가 leak 될 수 있음
       - 이로 인해 student는 masked input으로부터 infer 할 수 없는 information을 학습하게 되므로 biased prediction이 발생함
    2. 이를 방지하기 위해 논문은 student model이 unmasked part를 distilling 할 때와 동일한 masked input을 teacher model이 receive 하도록 하고, 이때 얻어지는 entire distillation loss는:
       (Eq. 6) $ \mathcal{L}(x)=\sum_{\ell}\alpha_{\ell}\left[\mathcal{L}_{m,\ell}(x)+\mathcal{L}_{u,\ell}(x)\right]$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\sum_{\ell}\frac{\alpha_{\ell}}{|M|}\sum_{i\in M}\left|\left| f_{i,\ell}^{t}(x)-f_{i,\ell}^{s}(\mu(x))\right|\right|_{2}+ \sum_{\ell}\frac{\alpha_{\ell}}{n-|M|}\sum_{i\notin M} \left|\left| f_{i,\ell}^{t}(\mu(x))-f_{i,\ell}^{s}(\mu(x))\right|\right|_{2}$
       - $\alpha_{\ell}$ : layerwise coefficient, $\mathcal{L}_{m,\ell}, \mathcal{L}_{u,\ell}$ : 각각 $\ell$-th layer의 masked loss, unmasked loss
  • 결과적으로 논문의 masking distillation strategy는 masked data의 unmasked representation과 unmasked data의 masked representation 모두를 distilling 함으로써 student의 knowledge acquisition을 guide 함

3. Experiments

- Settings

• Dataset : LibriSpeech
• Comparisons : HuBERT, LightHuBERT, DistilHuBERT, FitHuBERT, WavLM

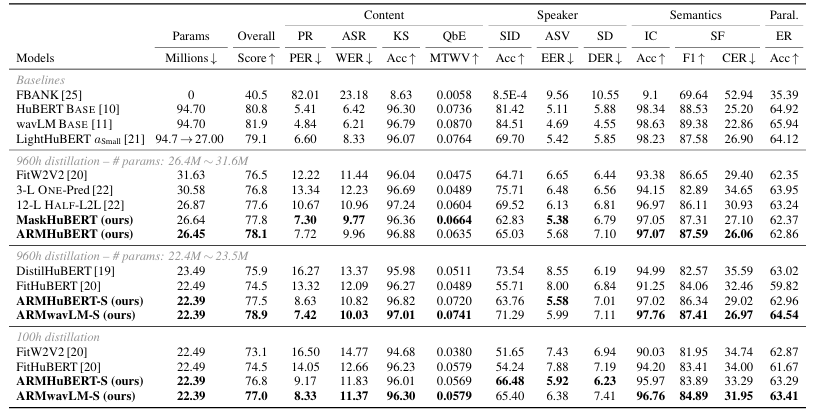
- Results

• 전체적으로 ARMHuBERT의 성능이 가장 뛰어남

Model 성능 비교

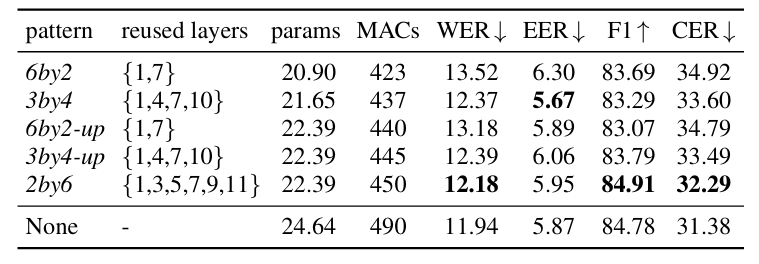
• Reusing Pattern
  • $2by6$ pattern을 사용했을 때 최상의 성능을 달성할 수 있음

Reusing Pattern

• Masking Strategy
  • 각 masking strategy는 성능 향상에 유효함

Ablation Study

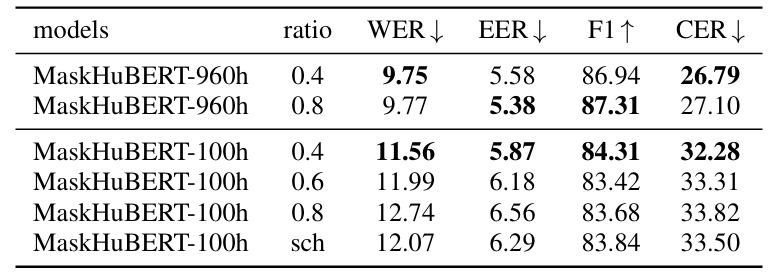
• Masking Ratio
  • $0.4$ ratio를 사용할 때 최적의 성능을 달성함

Masking Ratio