[Paper 리뷰] UniWav: Towards Unified Pre-Training for Speech Representation Learning and Generation

UniWav: Towards Unified Pre-Training for Speech Representation Learning and Generation

---

• Pre-training과 representation learning은 서로 다른 foundation model을 사용함
• UniWav
  • Pre-training, representation learning을 위한 unified encoder-decoder framework
  • Representation encoder와 generative decoder를 jointly learning
• 논문 (ICLR 2025) : Paper Link

---

1. Introduction

• Speech representation은 specific task를 excelling 하는 데 사용됨
  • 특히 HuBERT, Wav2Vec 2.0과 같은 pre-training method는 unlabeled speech로부터 self-supervised learning을 통해 speech representation을 학습함
  • 해당 representation model은 masked audio에서 추출된 output과 unmasked audio에서 추출된 output을 matching 하는 masked audio modeling을 주로 활용함
    1. Masked audio modeling을 통해 얻어진 representation은 phonetic, semantic content를 주로 capture 하므로 speaker timbre, acoustic environment와 같은 acoustic information을 반영하기 어려움
    2. 결과적으로 self-supervised representation은 classification, recognition task에서만 제한적으로 활용됨
  • 한편으로 SpeechFlow와 같이 generative model에 masked audio modeling을 적용하여 minimal supervision으로 downstream task에 transfer 할 수도 있음
    - BUT, pre-training과 generative method는 전체적으로 유사한 masked audio modeling을 활용함에도 불구하고, 여전히 개별적으로 설계되고 training 됨
  • 이때 representation learning, generation에 대한 unified pre-training framework를 구성하면 training overhead를 줄이고 discriminative, generative downstream application을 모두 지원할 수 있음 

-> 그래서 discriminative, generative task에 대한 unified pre-training framework인 UniWav를 제안

 

• UniWav 
  • Representation encoder와 learned representation으로 condition 된 flow matching decoder를 integrate 한 encoder-decoder framework
  • Encoder, decoder를 end-to-end manner로 jointly scratch training 함으로써 speech discriminative, generation task를 모두 지원

< Overall of UniWav >

• Speech representation learning, generation을 위한 unified pre-training framework
• 결과적으로 기존보다 뛰어난 성능을 달성

2. Method

• UniWav는 representation learning과 generative task를 unify 하는 encoder-decoder framework에 해당함
  • Input으로는 EnCodec과 같은 speech의 surface feature를 사용함
  • 이후 masked audio modeling을 통해 input에 대한 latent representation encoding과 speech generation을 jointly learning 함

Overview

- Representation Encoder

• Self-supervised learning은 unlabeled data의 input 자체에서 learning target을 derive 하여 representation을 학습함
  • 논문에서는 self-supervised learning을 위해 self-distillation과 online clustering을 채택함
  • $\mathbf{x}_{i}\in\mathbb{R}^{d}$를 speech의 input surface feature frame, $x=(\mathbf{x}_{1},\mathbf{x}_{2},...,\mathbf{x}_{L})$을 input audio frame sequence라고 하자
    1. 그러면 frame의 subset을 randomly mask 한 $M$을 Transformer encoder에 전달하여 output latent embedding $z=(\mathbf{z}_{1},\mathbf{z}_{2},...,\mathbf{z}_{L})$을 얻을 수 있음
       - $\mathbf{z}_{i}\in\mathbb{R}^{d}$
       
    2. 이때 encoder는 (Eq. 1)을 maximize 하여 teacher가 제공한 pseudo-label $y_{i}$를 predict 함:
       (Eq. 1) $\frac{1}{|M|}\sum_{i:\mathbf{x}_{i}\in M}\log p_{\phi}(y_{i}|\mathbf{z}_{i})$
       - $\phi$ : pseudo-label prediction head
    3. Pseudo-label을 derive 하는 teacher model은 encoder의 Exponential Moving Average (EMA) $\theta_{teacher}\leftarrow \gamma_{teacher}\theta_{teacher}+(1-\gamma_{teacher})\theta_{encoder}$와 같음
       - $\gamma_{teacher}$ : decay factor
       
  • 이때 encoder는 masked audio를 input으로 사용하고 teacher model은 masking이 없는 complete audio를 input으로 사용하여 input frame $\mathbf{x}_{i}$에 대해 pseudo-label을 derive 함:
    (Eq. 2) $y_{i}=\arg\min_{v\in V}|| \tilde{\mathbf{z}}_{i}-\mathbf{e}_{v}||_{2} $
    - $\tilde{\mathbf{z}}_{i}$ : teacher model output, $\mathbf{e}_{v}$ : size $V$ codebook의 codeword
  • 모든 codeword는 same pseudo-label을 share 하는 teacher output embedding의 EMA를 통해 update 됨:
    (Eq. 3) $\mathbf{s}_{v}\leftarrow \gamma_{code}\mathbf{s}_{v}+(1-\gamma_{code})\sum_{i:y_{i}=v}\tilde{\mathbf{z}}_{i}$
    $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,n_{v}\leftarrow\gamma_{code}n_{v} +(1-\gamma_{code})\sum_{i:y_{i}=v}1$
    $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathbf{e}_{v}\leftarrow\frac{\mathbf{s}_{v}}{n_{v}}$
    - $\gamma_{code}$ : decay factor, $\mathbf{s}_{v}\in\mathbb{R}^{d}$ : cluster sum으로써, randomly initialize 됨
    - $n_{v}$ : cluster size로써 $1$로 initialize 됨
  • 논문은 각 layer에 대해 (Eq. 1-3)을 repeating 하여 teacher model의 top-$K$ layer에 대한 pseudo-label을 고려하고, 이때 encoder의 complete loss function은:
    (Eq. 4) $\mathcal{L}_{encoder}=-\frac{1}{|K||M|}\sum_{i:\mathbf{x}_{i}\in M}\sum_{k\in K}\log p_{\phi_{k}}(y_{i}^{(k)}|\mathbf{z}_{i})$
    - $K$ : 각각 independent codebook을 가지는 teacher model layer의 index set
    - Prediction은 target layer $k$에 관계없이 $\mathbf{z}_{i}$를 사용하여 final layer에서 수행됨

- Flow Matching Decoder

• 논문은 decoder를 training 하기 위해 flow matching을 채택함
  • Flow matching은 unknow data distribution $q(x)$로부터 sample $x_{1}$을 생성하는 것으로써, prior distribution $p_{0}$와 target distribution $p_{1}\approx q$ 간의 path를 따라 $x$의 flow를 predict 함
    1. 여기서 flow는 Ordinary Differential Equation (ODE)를 통해 정의됨:
       (Eq. 5) $\frac{d}{dt}\phi_{t}(x)=v_{t}(\phi_{t}(x));\,\,\,\phi_{0}(x)=x$
       - $v_{t}:[0,1]\times \mathbb{R}^{d}\rightarrow \mathbb{R}^{d}$ : time-dependent vector field
       
    2. Variable change formula를 통해 path를 따라 timestep $t$에서 distribution $p_{t}$를 generate 할 수 있음
       - 이를 기반으로 (Eq. 5)를 $t=0$에서 $t=1$까지 iterative solve 하여 $p_{1}$을 sampling 함
  • 해당 framework 하에서 decoder는 path를 생성하는 target vector field $u_{t}$와 match 하는 time-dependent vector field $v_{t}(x;\theta_{decoder})$를 predict 하는 것을 목표로 함
    1. 이때 decoder output을 $u_{t}$에 regress 하는 naive flow matching은 target vector field $u_{t}$가 generally unknown이므로 intractable 함
       - 대신 real data sample $x_{1}$을 사용하여 tractable $p_{t},u_{t}$를 가진 $x$의 conditional flow를 구성할 수 있음
    2. 먼저 Optimal Transport (OT) conditional path는 mean $\mu_{t}(x)=tx_{1}$, standard deviation $\sigma_{t}(x)=1-(1-\sigma_{\min})t$가 time에 따라 linearly change 한다고 가정함
       - $\sigma_{\min}$은 $p_{1}(x|x_{1})$이 $x_{1}$ 주변에 center 되도록 sufficiently small 함
    3. 그러면 OT conditional flow는:
       (Eq. 6) $\phi_{t}^{OT}(x)=(1-(1-\sigma_{\min})t)x_{0}+tx_{1}$
       
    4. Tractable $p_{t}(x|x_{1})=\mathcal{N}(x|\mu_{t}(x_{1}),\sigma_{t}(x_{1})^{2}I)$와 $u_{t}(x|x_{1})=\frac{(x_{1}-(1-\sigma_{\min})x)}{(1-(1-\sigma_{\min})t)}$로부터 derive 되는 Conditional Flow Matching (CFM) objective는:
       (Eq. 7) $\mathbb{E}_{t,q(x_{1}),p_{0}(x_{0})}\left|\left| v_{t}\left(\phi_{t}^{OT}(x_{0});\theta_{decoder}\right)- \left(x_{1}-(1-\sigma_{\min})x_{0}\right)\right|\right|^{2}$
       - $p_{0}$ : standard Normal distribution, $t$ : $[0,1]$에서 uniformly sample 됨
       - CFM objective와 naive flow matching은 model에 대해 identical gradient를 share 하므로 (Eq. 5)는 trained CFM을 통해 solve 될 수 있음
  • 추가적으로 논문은 decoder를 encoder layer feature $z$의 weighted sum으로 condition 하여 decoder에 대한 complete loss function을 얻음:
    (Eq. 8) $\mathcal{L}_{decoder}=\mathbb{E}_{t,q(x_{1}),p_{0}(x_{0})}\left|\left| v_{t}\left(\phi_{t}^{OT}(x_{0}),z;\theta_{decoder}\right)- \left(x_{1}-(1-\sigma_{\min})x_{0}\right)\right|\right|^{2}$
  • Representation encoder와 마찬가지로 generative decoder는 $d$-dimensional latent를 가지는 Transformer encoder로 구성되고, 이때 decoder input은:
    (Eq. 9) $W_{0}v_{t}\left(\phi_{t}^{OT}(x_{0})\right)+z,\,\,\, \text{where}\,\, z=\sum_{i}W_{i}z^{(i)}$
    - $W_{0}\in\mathbb{R}^{d_{x}\times d}$ : noisy data projection layer, $W_{i}\in\mathbb{R}^{d\times d}$ : encoder $i$-th layer의 representation $z^{(i)}$에 대한 linear projection layer
    - 즉, decoder는 noise-injected audio feature $x$와 모든 encoder layer의 representation에 대한 learnable combination $z$를 input으로 사용함

- UniWav Framework

• UniWav는 end-to-end manner로 training 됨 
  • 이때 overall objective는 encoder obejctive (Eq. 4), decoder objective (Eq. 8)을 combine 하여 얻어짐:
    (Eq. 10) $\mathcal{L}_{encoder}+\lambda\mathcal{L}_{decoder}$
    - $\lambda=0.25$ : weighting scalar
  • HuBERT, WavLM 등은 teacher model로부터 representation을 iteratively learning 하는 반면, UniWav는 self-distillation과 online clustering을 사용하여 encoder, decoder를 scratch training 함
    - Pre-training 이후 encoder는 representation을 추출하는 stand-alone module로 사용할 수 있음

3. Experiments

- Settings

• Dataset : LibirLight
• Comparisons
  - Self-Supervised Representation : HuBERT, WavLM, Data2Vec, Data2Vec 2.0
  - Generative Model : SpeechFlow, VALL-E, VoiceBox
  - Speech Codec : EnCodec, DAC, SpeechTokenizer

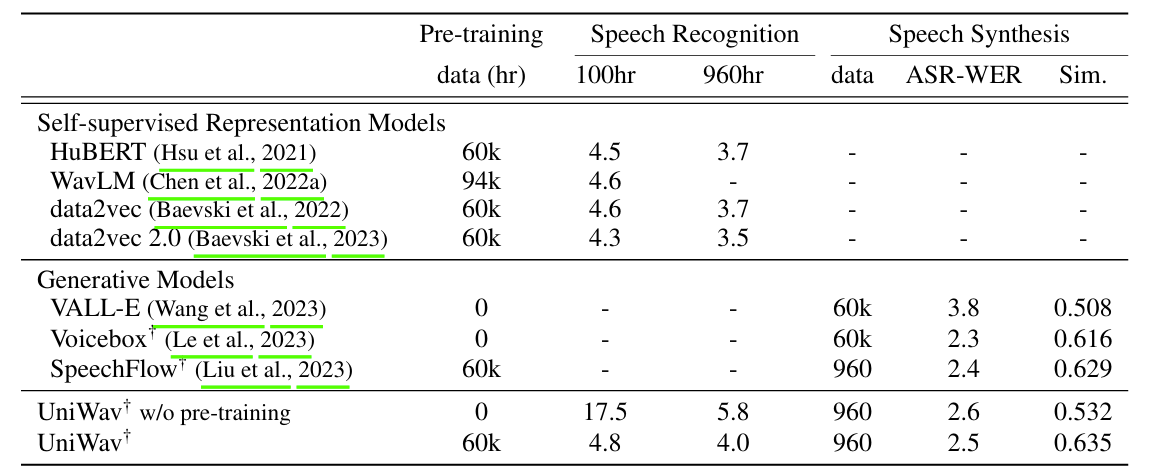
- Results

• 전체적으로 UniWav의 성능이 가장 우수함

Model 성능 비교

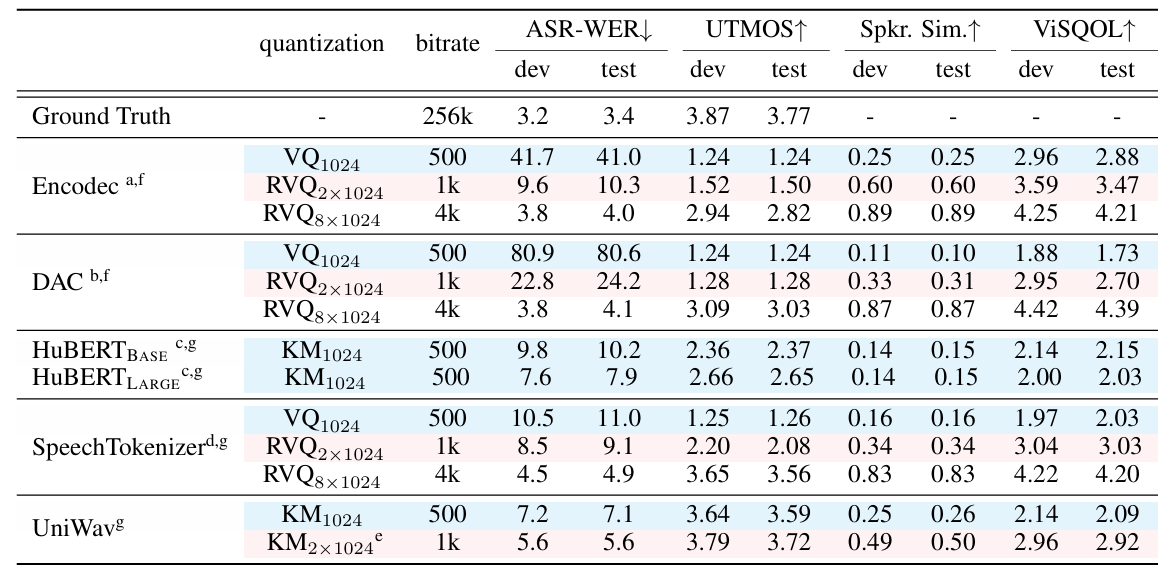
• Speech Tokenization
  • Tokenization을 위해 (Eq. 9)의 encoder representation $z$를 다음과 같이 replace 함:
    (Eq. 11) $ \bar{z}=W_{i}\underset{\text{semantic quantization}}{\underbrace{\arg\min_{q\in Q_{i}}\left|\left| z^{(i)}-q\right|\right|_{2}}}+\underset{\text{residual quantization (optional)}}{\underbrace{\arg\min_{q\in Q_{residual}}\left|\left| \sum_{j\neq i} W_{j}z^{(j)}-q\right|\right|_{2} }}$
  • Speech tokenization 측면에서도 UniWav의 성능이 가장 뛰어남

Speech Tokenization

• Scaling Encoder and Decoder
  • Shallow encoder로 speech recognition을 수행하면 WER이 저하됨
  • Speech generation의 경우 shallow encoder를 사용할 때 encoder depth가 큰 영향을 미침

Encoder, Decoder Scale 비교 (좌) Recognition (우) In-Context TTS

• Mutual Information Between Representation and Labels
  • Latter layer에서 UniWav는 HuBERT에 비해 phone에 대한 Mutual Information (MI)가 낮음
  • Speaker label에 대한 MI는 대부분의 layer에서 UniWav가 더 높게 나타남

Mutual Information (좌) Phone (우) Label