[Paper 리뷰] CCC-Wav2Vec 2.0: Clustering Aided Cross Contrastive Self-Supervised Learning of Speech Representations

CCC-Wav2Vec 2.0: Clustering Aided Cross Contrastive Self-Supervised Learning of Speech Representations

---

• Self-Supervised Learning은 unlabeled data를 효과적으로 활용할 수 있음
• CCC-Wav2Vec 2.0
  • Clustering과 Augmentation-based Cross-Contrastive loss를 self-supervised objective로 활용
  • 이를 통해 pre-training의 robustness를 향상
• 논문 (SLT 2023) : Paper Link

---

1. Introduction

• Self-Supervised Learning (SSL)은 unlabeled data에서 high-level representation을 학습할 수 있음
  • 대표적으로 Wav2Vec, HuBERT, WavLM 등은 SSL을 위해 contrastive learning을 통한 instance discrimination, masked prediction을 통해 Masked Acoustic Modeling (MAM)을 수행함
  • BUT, SSL은 여전히 low resource regime에 대해서는 useful representation을 학습하기 어려움
    1. 한편으로 limited unlabeled data를 위해 Wav2Vec-Aug는 data augmentation strategy를 활용함
    2. 이때 specific augmentation을 통해 noisy environment에 대한 robustness를 향상할 수 있음
  • 특히 contrastive learning에서 same data의 augmented view에 대한 agreement를 maximize 하면 더 나은 representation을 학습할 수 있음
    1. BUT, Spoken Language Processing (SLP)에서 contrastive learning에 대한 neagtive sample choice는 잘 활용되지 않음
       - 대부분 anchor point $x$가 주어지면 negative sample $x_{i}^{-}$는 training data에서 단순히 random sample 되므로 negative sample이 learned representation에 얼마나 informative 한 지를 고려하지 않음
    2. 이를 위해서는 population에서 weak non-informative negatives를 identify하고 loss computation에서 해당 negatives의 impact를 reduce 해야 함

-> 그래서 Wav2Vec 2.0 Contrastive Learning task에 informative negatives를 반영할 수 있는 CCC-Wav2Vec 2.0을 제안

 

• CCC-Wav2Vec 2.0
  • Original sample에 대한 augmentation을 도입하고 해당 representation을 사용하여 Wav2Vec 2.0에 auxiliary Cross-Contrastive loss를 add
  • Clustering module을 통해 negative example을 segregate 하고 contrastive learning task에서 weak non-informative example의 impact를 control

< Overall of CCC-Wav2Vec 2.0 >

• Wav2Vec 2.0을 기반으로 Cross-Contrastive loss, Clustering module을 적용한 speech SSL model
• 결과적으로 기존보다 뛰어난 성능을 달성

2. Method

- Cross-Contrastive Learning

• 논문은 pre-training approach에 robustness를 반영하기 위해 speech sample에 대한 augmentation을 수행함
  • Audio sample $X$가 주어지면, augmentation을 적용하여 augmented sample $X'$을 얻음
    1. 해당 $X,X'$을 Wav2Vec 2.0에 전달하여 quantized representation $Q_{t},Q'_{t}$와 context representation $C,C'$을 얻음
       - $t$ : masked time step
       
    2. 이때 quantized representation은 masked region에 해당하는 unmasked latent representation에 대해서만 compute 됨
       - 특히 original, augmented sample은 cross-contrastive loss computation을 위해 same masked index (time step)을 share 함
    3. Wav2Vec 2.0의 경우, standard contrastive loss는 각 masked time step $t$에 대해 다음과 같이 정의됨:
       (Eq. 1) $ \mathcal{L}_{c}=-\log \frac{\exp\left(\text{sim}(c_{t},q_{t})/\kappa\right)}{\sum_{\tilde{q}\sim Q_{t}}\exp\left(\text{sim}(c_{t},\tilde{q}_{t})/\kappa\right)}$
       - $c_{t}\in C, q_{t}\in Q_{t}$, $\kappa$ : temperature
       - $\text{sim}(\mathbf{m},\mathbf{n})=\mathbf{m}^{\top}\mathbf{n}/|| \mathbf{m}||\,||\mathbf{n}||$ : context, quantized representation 간의 cosine similarity
       - $\tilde{q}_{t}$ : $Q_{t}$에서 sample 된 특정 수의 example로써, distractor/negative example에 해당함 (여기서 논문은 $Q_{t}$의 모든 frame을 negative example로 사용하지는 않음)
       
  • Augmentation으로부터 representation이 주어지면, 다음과 같은 loss term을 얻을 수 있음:
    (Eq. 2) $\mathcal{L}_{cross}=-\log \frac{\exp\left(\text{sim}(c_{t},q'_{t})/\kappa\right)}{\sum_{\tilde{q}'\sim Q'_{t}}\exp\left(\text{sim}(c_{t},\tilde{q}')/\kappa\right)}$
    (Eq. 3) $\mathcal{L}_{cross'}=-\log \frac{\exp\left(\text{sim}(c'_{t},q_{t})/\kappa\right)}{\sum_{\tilde{q}'\sim Q_{t}}\exp\left(\text{sim}(c'_{t},\tilde{q})/\kappa\right)}$
    - $c'_{t}\in C', q'_{t}\in Q'_{t}$
    - (Eq. 2), (Eq. 3)은 original과 quantized representation 간의 contrastive loss, masked time step에 대한 contrastive loss와 같음
  • 최종적으로 얻어지는 overall cross-contrastive loss $\mathcal{L}_{cc}$는:
    (Eq. 4) $\mathcal{L}_{cc}=\alpha\mathcal{L}_{c}+\beta\mathcal{L}_{cross}+\gamma \mathcal{L}_{cross'}$
    - $\alpha, \beta,\gamma$ : hyperparameter
  • $\mathcal{L}_{cc}$로 pre-training 된 model의 성능은 augmentation choice에 따라 달라짐

- Clustering Module

• Clustering module은 weakly informative negatives set을 identify 하고 contrastive loss computation에서 negatives set의 effect를 diminish 하는 것을 목표로 함
• Need for Clustering
  • Negative example은 quantized representation $Q_{t}$로부터 얻어지므로, 논문은 $Q_{t}$의 entire frame set에 대해 clustering을 수행함
    1. 이때 $Q_{t}$의 frame은 product quantization을 통해 compute 된 discrete representation으로 구성되므로, population에서 randomly drawn 된 negative example은 same class를 represent 할 수 있음
       - Speech는 consecutive speech frame이 same phone, sound를 represent 할 수 있는 quasi-stationary nature를 가지기 때문
    2. 따라서 논문은 negative example elimination을 적용하여 해당 문제를 완화하고 clustering을 통해 informative negatives를 제공하는 것을 목표로 함
  • 한편으로 Wav2Vec 2.0의 product quantization은 size가 $320$인 2개의 codebook을 사용하므로 가능한 총 discrete representaiton은 $320\times 320=102400$과 같음
    1. 이러한 huge discrete representation에서 similar frame에 대해 same discrete representation을 가지는 quantization $q_{t}$를 find 하는 것은 어려움
    2. 따라서 definite similarity를 identify 하기 위해 cosine distance를 기반으로 한 clustering module을 채택함
• Cluster Factor $CF$
  • 논문은 cosine distance를 metric으로 하여 $Q_{t}$에 $k$-means clustering을 적용함
    1. 이때 각 speech sample의 mini-batch에서 동일한 수의 frame을 keeping 하기 위해 padding을 도입함
    2. BUT, audio 당 frame 수는 mini-batch 마다 달라질 수 있으므로 cluster 수를 fix 하기 어려움
       - 만약 cluster 수를 fix 하는 경우 sub-optimal clustering result가 나타남
  • 해당 문제를 해결하기 위해, hyperparameter로써 clustering factor $CF$를 도입함
  • Clustering은 각 mini-batch에서 separately perform 되므로 mini-batch의 audio frame 수에 따라 cluster 수를 fix 할 수 있기 때문
    1. 먼저 audio sample의 mini-batch가 주어졌을 때, padding 이후 audio 당 frame 수를 $NF$라고 하자
    2. 그러면 해당 mini-batch의 각 audio에 대한 clustering module의 cluster 수는 $\text{ceil}(NF/CF)$와 같음
       - $CF=1$일 때는 clustering이 수행되지 않으므로 standard Wav2Vec 2.0과 같음
• Scale Factor $SF$
  • $Q_{t}$에서 clustering을 수행한 다음, positive sample $q_{t}$가 속하는 cluster를 identify 함
    1. 즉, $q_{t}$가 속하는 cluster를 $K$라고 했을 때 cluster $K$에 속하는 negative example의 influence를 control 하는 것을 목표로 함
       - Influence는 (Eq. 1)의 contrastive loss computation에 미치는 영향을 의미
    2. 여기서 negative sample에 사용되는 metric은 cosine similarity이므로 influence control은 cosine similarity value를 control하는 것과 같음
  • 이를 위해 논문은 $K$ 내의 negative example에 대한 cosine similarity $c_{t}$를 scaling factor $SF$만큼 scale down 함 
    1. Sampled negatives set을 $Q^{*}$라고 하면, $Q^{*}=\{\tilde{q}\sim Q_{t}\}$와 같음
    2. $Q^{*}$의 sample을 $q$라고 할 때, contrastive loss는 다음과 같이 주어짐:
       (Eq. 5) $ \mathcal{L}_{c}=-\log \frac{e^{\left(\text{sim}(c_{t},q_{t})/\kappa\right)}}{\sum_{q\in K}e^{\left(\text{sim} (c_{t},q)\cdot SF/\kappa\right)}+\sum_{q\notin K} e^{\left(\text{sim}(c_{t},q)/\kappa\right)}}$
  • (Eq. 5)에서 positive example과 동일한 cluster를 share 하는 negatives의 influence는 scalar $SF$에 의해 control 됨
    - $SF=1$일 때, (Eq. 5)는 (Eq. 1)의 standard contrastive loss와 같음
    - $SF=-\infty$일 때, positive와 동일한 cluster에 있는 모든 negatives는 completely discard 됨

CCC-Wav2Vec 2.0

- CCC-Wav2Vec 2.0

• CCC-Wav2Vec 2.0은 앞선 cross-contrastive setup과 clustering module을 integrate 함
  • Clustering module이 original, augmented sample의 quantized representation을 clustering 한 다음, scaling factor $SF$는 positive와 같은 cluster에 속하는 negative example에 적용됨 
  • 이때 cluster는 quantized representation의 color shade로 identify 할 수 있음 
    1. 위 그림에서 $q_{5}$는 positive example $q_{3}$와 동일한 cluster에 속하므로 $SF$가 적용되고, $q'_{1}$도 positive example $q'_{3}$와 동일한 cluster에 속하므로 $SF$가 적용됨
    2. 한편으로 위 그림에서 $q'_{4}$는 $q'_{3}$과 동일한 cluster에 속하지만 $SF$가 적용되지 않음
       - $q'_{4}$는 potential negative example이지만, negative sampling process에서 sampling 되지 않았기 때문
       - 즉, $q'_{4}$는 loss computation에 포함되지 않으므로 $SF$를 적용하지 않음
  • 결과적으로 CCC-Wav2Vec 2.0에 대한 loss computation은 (Eq. 1)~(Eq. 4)을 따르는 대신, (Eq. 5)와 같이 scaling factor $SF$를 포함해야 함 

3. Experiments

- Settings

• Dataset : LibriSpeech
• Comparisons : Wav2Vec 2.0

- Results

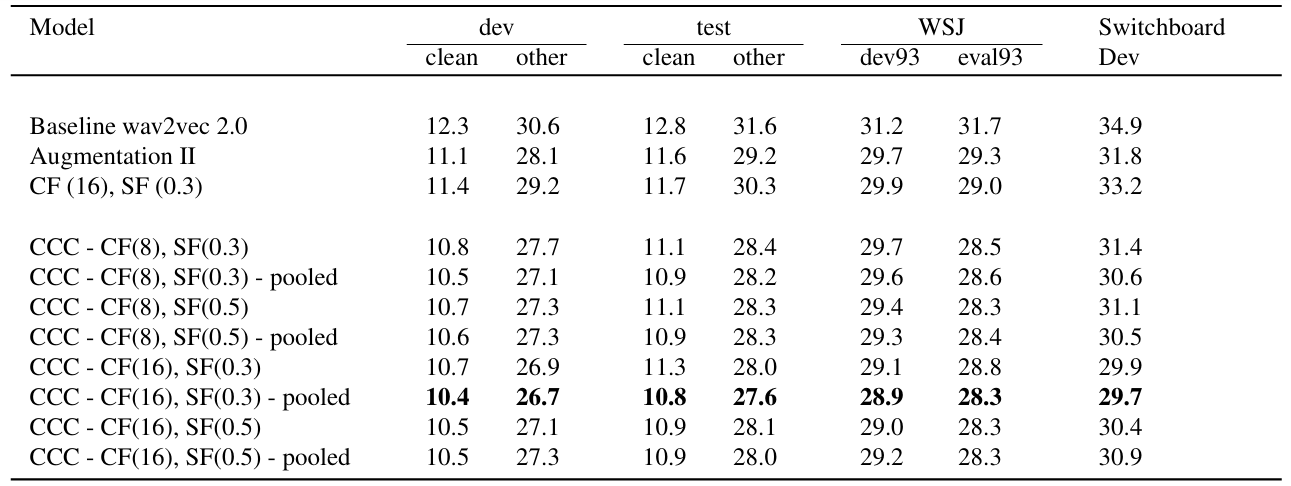
• Wav2Vec 2.0에 대해 (Eq. 1)의 $\alpha, \beta, \gamma$를 각각 $1,0.5,0.5$로 설정한 Augmentation II를 사용하는 경우, 최적의 성능을 얻을 수 있음

Data Augmentation 설정 별 성능

• Clustering의 경우 Cluster Factor $CF$, Scale Factor $SF$를 각각 $16, 0.3$으로 설정할 때 최적의 성능을 달성함

Cluster 설정 별 성능

• 해당 설정을 기반으로 CCC-Wav2Vec 2.0은 기존보다 우수한 성능을 달성함

Model 성능 비교

• SUPERB Evaluation
  • SUPERB framework에 대해서도 뛰어난 성능을 보임

SUPERB 성능