[Paper 리뷰] nnSpeech: Speaker-Guided Conditional Variational Autoencoder for Zero-Shot Multi-Speaker Text-to-Speech

nnSpeech: Speaker-Guided Conditional Variational Autoencoder for Zero-Shot Multi-Speaker Text-to-Speech

---

• Multi-speaker text-to-speech를 활용하기 위해서는 어려움이 많음
• nnSpeech
  • Fine-tuning 없이 하나의 adpatation utterance만을 사용하여 새로운 speaker voice를 합성할 수 있는 zero-shot multi-speaker 모델
  • Speaker-guided conditional vairational autoencoder를 활용하여 speaker, content information을 모두 포함하는 variable $Z$를 생성 
  • Latent variable $Z$의 분포는 reference mel-spectorgram과 phoneme을 condition으로 하는 다른 variable에 의해 근사됨
• 논문 (ICASSP 2022) : Paper Link

---

1. Introduction

• 최근 neural Text-to-Speech (TTS)의 발전으로 보다 자연스러운 음성을 합성할 수 있지만, 대부분 single-speaker TTS 모델로 제한되어 있어 multi-speaker 시나리오로 확장하기 어려움
  • Multi-speaker TTS는 few-shot data를 활용하여 fine-tuning을 수행하는데, 이 방식에는 2가지 큰 한계점이 있음
    1. Fine-tuning을 수행하면 각 speaker에 대해 모델을 새로 학습시켜야 하기 때문에 memory 비용이 증가함
    2. Speaker 수가 많은 경우, fine-tuning은 사실상 불가능함
  • Zero-shot multi-speaker TTS는 이러한 fine-tuning 없이 직접 음성을 합성할 수 있다는 장점이 있음
    - 이를 위해 pre-trained speaker verification model을 사용하여 speaker information을 추출하거나,
    - Speaker encoder와 TTS 모델을 jointly optimize 하여 speaker representation을 향상할 수 있음
  • BUT, TTS 모델을 guide하는 speaker representation을 추출하는 것은 여전히 어렵고, zero-shot TTS는 unseen speaker에 대해서도 잘 동작할 수 있는 generic model을 학습해야 함
    

-> 그래서 zero-shot TTS를 위해 conditional variational autoencoder를 사용하는 nnSpeech를 제안

 

• nnSpeech
  • Fine-tuning 없이 새로운 speaker의 음성을 합성하는 zero-shot multi-speaker TTS 모델
  • Phoneme과 speaker의 condition을 따르는 latent variable $Z$의 분포가 reference mel-spectrogram과 phoneme에 condition 된 또 다른 variable을 통해 근사될 수 있다는 점을 활용
  • 이를 위해 Conditional Variational AutoEncoder (CVAE)를 수정하여 speaker-guided CVAE로 확장

< Overall of nnSpeech >

• Fine-tuning 없이 하나의 adpatation utterance만을 사용하여 새로운 speaker voice를 합성할 수 있는 zero-shot multi-speaker 모델
• Speaker-guided CVAE를 활용하여 speaker와 content information을 모두 포함하는 variable $Z$를 생성
• 결과적으로 multi-speaker TTS 환경에서 우수한 성능을 달성

2. Method

- VAE and CVAE

• VAE는 autoencoder neural network architecture의 한 종류
  • Encoder network는 input data $X$가 주어지면, latent space variable $Z$에 대한 conditional 분포 $q_{\phi}(Z|X)$를 나타내고,
    - Decoder network는 input vector $Z$가 주어지면 생성된 data $X$에 대한 분포 $p_{\theta}(X|Z)$를 나타냄
    - 이에 따라 VAE는 $p_{\theta}(Z|X)\propto p_{\theta}(X|Z)p(Z)$와 일치하는 $q_{\phi}(Z|X)$를 만들기 위해 training data로부터 parameter를 학습함
  • 여기서 data $X$의 log marginal 분포는 Evidence Lower BOund (ELBO)로써 나타남:
    (Eq. 1) $\mathcal{L}(\theta,\phi;X)=\mathbb{E}_{q_{\phi}(Z|X)}[\log (p_{\theta}(X|Z))]-KL[q_{\phi}(Z|X)||p(Z)]$
    - $KL(q_{\phi}|p_{\theta})$ : KL-divergence
    
  • 따라서 ELBO를 최대화함으로써 $p_{\theta}(Z|X)$와 $q_{\phi}(Z|X)$ 간의 KL-divergence를 최소화할 수 있고, 이는 (Eq. 1)을 통해 reduce 됨
    - $p_{\theta}(Z|X), q_{\phi}(Z|X)$를 모델링하는 방법은, diagonal covariance matrix를 사용하여 normal 분포를 가정하는 것
    - 여기서 prior 분포 $p(Z)$는 필요로 하는 가정에 따라 specific form으로 설계될 수 있음
  • (Eq. 1)에서 첫 번째 term은 autoencoder reconstruction error이고, 두 번째 term은 KL-divergence $q_{\phi}(Z|X)=\mathcal{N}(Z|\mu_{\phi}(x),\sigma_{\phi}(x)), \,\, p(Z)=\mathcal{N}(Z|0,I)$
    - Reparameterization $z=\mu_{\phi}(x)+\sigma_{\phi}\odot \epsilon, \,\epsilon\sim\mathcal{N}(\epsilon | 0,I)$를 사용하면 $q_{\epsilon}(Z|X)$에서 직접 sampling 하는 대신 분포에서 $\epsilon$을 sampling 하여 $z$를 생성할 수 있음
    - 결과적으로 $\theta$에 대한 lower bound의 gradient를 계산할 수 있음
• Conditional VAE (CVAE)는 VAE의 확장으로써 주어진 $C$에 대한 $X$의 conditional log-likelihood를 최대화하도록 학습됨
  • 이때 variational lower bound는:
    (Eq. 2) $\mathcal{L}(\theta,\phi;X,C)=\mathbb{E}_{q_{\phi}(Z|X,C)}[\log (p_{\theta}(X|Z,C))]-KL[q_{\phi}(Z|X,C)||p_{\theta}(Z|C)]\leq \log p_{\theta}(X|C)$
    - VAE와 마찬가지로 prior 분포 $p(Z|C)$는 요구사항에 따라 설계될 수 있음
  • 여기서 latent $Z$가 $C$와 independent 하다고 가정하면 $p_{\theta}(Z|C)=p(Z)$
  • Network architecture 측면에서 VAE와 CVAE의 차이점은, encoder와 decoder가 auxiliary variable $C$를 추가 input으로 사용한다는 것

CVAE와 Speaker-Guided CVAE

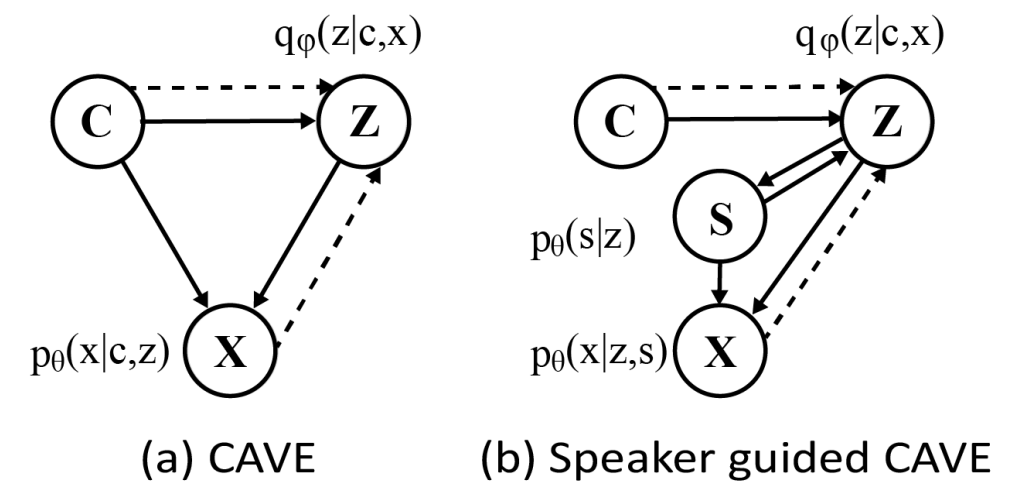
- Speaker-Guided CVAE for Zero-Shot Multi-Speaker TTS

• 대부분의 multi-speaker TTS 모델은,
  • Phoneme information을 latent variable $Z$로 encoding 하는 phoneme encoder, $Z$로부터 mel-spectrogram을 생성하는 decoder, timbre를 제어하기 위해 $Z$에 추가되는 speaker representation으로 구성됨
    - Speaker representation은 jointly-optimize 된 look-up embedding table이나 pre-trained speaker verification system으로 얻어짐
  • nnSpeech는 CVAE를 도입하여 multi-speaker TTS를 모델링함
    1. Multi-speaker TTS를 위한 CVAE는 mel-spectrogram, phoneme, latent variable로 구성됨
    2. 이때 더 나은 feature fusion을 위해 $X, C$를 mel-encoder와 phoneme encoder의 output으로 정의
       - Mel-encoder는 AdaIN-VC의 speaker encoder를 활용
       - Phoneme encoder와 Mel-decoder는 FastSpeech2를 활용
• 먼저 conditional 분포 $p(X,Z|C)=p_{\theta}(X|C,Z)p_{\theta}(Z|C)$를 정의하고, $p_{\theta}(X|C,Z)$, $p_{\theta}(Z|C)$는 각각 mel-decoder와 prior encoder를 통해 모델링 된다고 하자
  • 이때 true posterior $p_{\theta}(Z|C)$를 근사하기 위해 $q_{\phi}(Z|C,X)$를 사용할 수 있음
    - BUT, mel-spectrogram을 reconstruct 하기 위해서 latent variable $Z$가 speaker information으로 구성되어야 하므로 counterintuitive 함
  • 따라서 nnSpeech는 $p_{\theta}(Z|C)=p_{\theta}(X|Z,S)$와 같이 latent $Z$의 prior가 speaker representation $S$에 기반한다고 가정하고 speaker-guided CVAE를 도입함
    - 이후 $q_{\phi}(Z|C,X)$를 사용하여 $p_{\theta}(Z|C,S)$를 근사함
  • 이때 latent $Z$가 $C$의 전체 information을 포함한다고 가정하므로 $p_{\theta}(X|C,Z,S) = p_{\theta}(X|Z,S)$이고, 결과적으로 speaker-guided CVAE에서 conditional 분포는 다음과 같이 수정됨:
    $p(X,Z|C,S)=p_{\theta}(X|Z,S)p_{\theta}(Z|C,S)$
• Latent variable $z$가 diagonal covariance matrix를 기반으로 Gaussian 분포를 따른다고 하자
  • 즉, $q_{\phi}(Z|C,X)\sim \mathcal{N}(\mu_{1},\sigma^{2}_{1}I), \, p_{\theta}(Z|C,S)\sim \mathcal{N}(\mu_{2},\sigma_{2}^{2}I)$
  • 그러면 recognition network $q_{\phi}(Z|C,X)$와 prior network $p_{\theta}(Z|C,S)$는:
    (Eq. 3) $\begin{bmatrix} \mu_{1} \\ \ln \log \sigma^{2}_{1} \end{bmatrix} = \mathbf{MLP}_{q_{\phi}}(\begin{bmatrix} X \\ C \end{bmatrix})$, $\begin{bmatrix} \mu_{2} \\ \ln \log \sigma^{2}_{2} \end{bmatrix} = \mathbf{MLP}_{p_{\theta}}(\begin{bmatrix} C \\ S \end{bmatrix})$
  • Reparameterization trick은 분포 $\mathcal{N}(\mu_{1},\sigma_{1}^{2}I)$, $\mathcal{N}(\mu_{2},\sigma_{2}^{2}I)$에서 $Z_{1},Z_{2}$를 sampling 하는 데 사용됨
    - 이를 통해 mel-decoder network $p_{\theta}(X|Z,S)$를 기반으로 mel-spectrogram $X$를 생성할 수 있음
  • 추가적으로 network를 통해 $\hat{S} =\mathbf{MLP}_{S}(Z)$를 예측하여 추론 시 speaker embedding $S$는 예측된 $\hat{S}$로 대체
    - 최종적으로 nnSpeech는 HiFi-GAN을 사용하여 음성을 생성함

Overall of nnSpeech

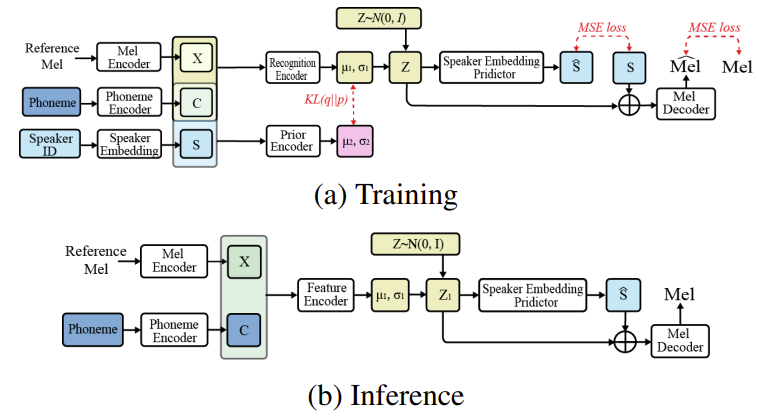
- Loss Functions

• nnSpeech는
  • 다음의 modified ELBO를 최대화하는 것으로 학습됨:
    (Eq. 4) $\mathcal{L}(\theta,\phi;X,C,S)=\mathbb{E}_{q_{\phi}(Z|X,C)}[\log (p_{\theta(X|Z,S)})]+\mathbb{E}_{q_{\phi}(Z|X,C)}[\log (p_{\theta}(S|Z))]-KL[q_{\phi}(Z|X,C)||p_{\theta}(Z|C,S)]$
    - 첫 번째, 두 번째 term은 각각 mel-spectrogram과 speaker embedding에 대한 기댓값이고, 세 번째 term은 KL-divergence
    - 따라서 위 식을 최대화한다는 것은 추정의 Mean Squared Error (MSE)를 최소화하는 것과 동일함
    
  • 결과적으로 ELBO의 최대화는 mel loss, speaker loss, KL loss 3가지의 loss를 최소화함으로써 구현될 수 있음
    1. 이때 mel loss와 speaker loss는 각각:
       (Eq. 5) $\mathcal{L}_{mel}=\mathbb{E}[||X-\hat{X}||_{2}], \,\,\, \mathcal{L}_{spk}=\mathbb{E}[||S-\hat{S}||_{2}]$
       - $X$ : mel-spectrogram, $S$ : speaker embedding vector
       
    2. KL loss는:
       (Eq. 7) $\mathcal{L}_{kl}=\frac{1}{2}\log \frac{|\Sigma_{2}|}{|\Sigma_{1}|}-n+tr(\Sigma_{2}^{-1}\Sigma_{1})+(\mu_{1}-\mu_{2})^{T}\Sigma_{2}^{-1}(\mu_{1}-\mu_{2})$
       - $\mu_{1}, \Sigma_{1}, \mu_{2},\Sigma_{2}$는 Gaussian 분포 $p_{\theta},q_{\phi}$를 나타냄
  • 따라서 total loss는:
    (Eq. 8) $\mathcal{L}=\alpha *\mathcal{L}_{mel}+\beta*\mathcal{L}_{spk}+\gamma*\mathcal{L}_{kl}$
    - $\alpha, \beta$는 1로 두고, $\gamma$는 hyperparameter로 최적값을 탐색

3. Experiments

- Settings

• Dataset : LibriTTS, AISHELL3, LJSpeech
• Comparisons : X-Vector, StyleSpeech

- Results

• Performance
  • MOS 측면에서 nnSpeech가 가장 우수한 성능을 보이는 것으로 나타남
  • 추가적으로 decoder를 fine-tuning 하는 경우, 더 나은 성능을 얻을 수 있음

성능 비교 결과

• Mel-Cepstral Distortion (MCD)를 통한 정량적인 평가 측면에서도 nnSpeech는 가장 우수한 성능을 보임

정량적인 성능 비교

• MCD Under Vary Adaptation Data
  • AISHELL3에 대해 다양한 adaptation data를 사용하여 MCD를 비교
  • Adaptation data가 증가함에 따라 MCD가 감소하는 것으로 나타남
    - 즉, nnSpeech는 adaptation data에 대해 speaker information을 효과적으로 추출할 수 있음

Adaptation Voice 별 MCD 비교

• Hyperparameter Analysis
  • nnSpeech는 $\gamma$를 0.0005로 설정했을 때 가장 우수한 성능을 보임
  • 이는 KL divergence가 $\mathcal{L}_{mel}, \mathcal{L}_{spk}$ 같은 MSE loss 보다 항상 크기 때문

Hyperparameter Setting 비교

• Analysis on the Model Architecture
  • 다음의 2가지 architecture를 nnSpeech와 비교
    1. Content information $C$를 latent variable $Z$에 추가한 모델
    2. 예측된 speaker embedding $C$를 latent $Z$에 추가하지 않는 모델
  • 결과적으로 두 architecture 모두 nnSpeech 보다 낮은 성능을 보임

Architecture Ablation 결과