[Paper 리뷰] Direct Design of Biquad Filter Cascades with Deep Learning by Sampling Random Polynomials

Direct Design of Biquad Filter Cascades with Deep Learning by Sampling Random Polynomials

---

• Arbitrary magnitude response와 match 하도록 Infinite Impulse Response filter를 설계하는 것은 어려움
  - Yule-Walker method는 효율적이지만 high-order response를 정확하게 match 하지 못함
  - Iterative optimization은 우수한 성능을 보이지만 initial condition에 민감
• IIRNet
  • 수백만개의 random filter에 대해 학습된 neural network를 사용하여 target magnitude response에서 filter coefficient space로의 direct mapping을 학습
  • 원하는 response에 따라 filter coefficient를 빠르고 정확하게 추정 가능
• 논문 (ICASSP 2022) : Paper Link

---

1. Introduction

• Infinite Impulse Response (IIR) filter는 tone matching, feedback reduction, room compensation 등에 사용됨
  • 고전적인 digital IIR filter는 minimum passband ripple을 갖는 lowpass filter로 설계됨   
  • 한편 arbitrary magnitude나 phase response를 처리하는 digital IIR filter는
    - Modified Yule-Walker (MYW), Least Square, Linear Programming, Steiglitz McBride, Gradient-based optimization 등을 활용함
  • BUT, 위 방식들은 높은 accuracy와 빠른 추정, 두 가지 모두를 달성하지 못함
    1. MYW는 high-order response에 대해서는 부정확한 결과를 생성함
       - 대신 적은 수의 operation 만으로도 빠르게 결과를 얻을 수 있음
    2. Iterative method는 높은 accuracy를 얻을 수 있지만, customized loss function이 필요하고 gradient 업데이트로 인해 계산 비용이 높음
       - 특히 optimization 과정은 일반적으로 non-convex 하기 때문에 initial condition에 민감하고 local minima 문제를 겪을 수 있음
  • 이를 해결하기 filter 설계에 deep learning approach를 도입하는 추세임
    - 대표적으로 RNN을 활용해 arbitrary filter를 학습할 수 있지만, recursive 특성으로 인해 학습이 느림
    - 대신 원하는 magnitude response가 주어지면 parameter를 직접 추정하여 iterative optimization 문제를 해결

-> 그래서 주어진 arbitrary magnitude response에서 IIR filter coefficient로의 직접 mapping을 학습하는 IIRNet을 제안

 

• IIRNet
  • Magnitude response가 주어진 biquad cascade 추정을 위해, randomly generated filter로 학습된 network를 도입
  • Random polynomial의 behavior를 활용하여 다양한 random filter를 생성

< Overall of IIRNet >

• IIRNet을 통해 arbitrary magnitude response와 match 되는 neural network biquad filter cascade estimation의 안정적인 학습을 구현
• 다양한 범위의 random polynomial family에서 random filter를 생성하는 training regime을 제시
• 결과적으로 run-time과 accuracy 측면 모두에서 우수한 성능을 달성

Overall of IIRNet

2. Background

- Digital IIR Filters with Biquad Representation

• $N$-th degree digital IIR filter는,
  • 아래의 transfer function으로 charcterize될 수 있음:
    (Eq. 1) $H(z)=\frac{b_{0}+b_{1}z^{-1}+...+b_{N}z^{-N}}{a_{0}+a_{1}z^{-1}+...+a_{N}z^{-N}}$
    - $b_{i},a_{i} \in \mathbb{R}$
  • Numerical stability를 위해, 해당 filter는 $K$개의 cascaded second-order biquad section $H(z) =\prod_{k=0}^{K-1}H_{k}(z)$로 구현되고, 여기서 $H_{k}(z)$는:
    (Eq. 2) $H_{k}(z)=g\frac{1+b_{1,k}z^{-1}+b_{2,k}z^{-2}}{1+a_{1,k}z^{-1}+a_{2,k}z^{-2}}$
    - 이때 각 biquad의 poles와 zeros가 complex plane의 unit circle 내에 속하면 digital IIR filter는 minimum phase라고 함
  • 해당 filter의 magnitude response $|H(e^{i\omega})|$는 complex plane의 unit circle을 따라 $H(z)$를 계산하고, 해당 결과의 magnitude를 취하여 얻을 수 있음:
    (Eq. 3) $|H(e^{i\omega})|=\left| \frac{b_{0}+b_{1}e^{-i\omega}+...+b_{N}e^{-iN\omega}}{a_{0}+a_{1}e^{-i\omega}+...+a_{N}e^{-iN\omega}}\right|$
  • 실질적으로는 해당 magnitude response의 logarithm에 관심을 둠:
    (Eq. 4) $\log (|H(e^{i\omega})|)=G+\log \left(\prod_{k=0}^{K-1}\left| \frac{1+b_{1,k}e^{-i\omega}+b_{2,k}e^{-2i\omega}}{1+a_{1,k}e^{-i\omega}+a_{2,k}e^{-2i\omega}}\right| \right)$

(A)Normal Coefficient (B)Normal Biquad (C)Uniform Disk (D)Uniform Magnitude (E)Characteristic Polynomial (F)Uniform Parametric EQ

- Random Polynomials

• Neural network filter estimator의 training은, random digital IIR filter의 dataset 생성에 의존함
  • Training을 위한 random filter sampling은 generalization에서 중요한 역할을 함
  • Random filter 생성에는 (Eq. 1)에서 설명된 polynomial의 random sampling이 포함됨
• 이를 위해 even $N$-degree random polynomial을 sampling 하는 방법을 정의
  1. Polynomials with Normal Coefficients
     • $N$-degree polynomial $c_{N}x^{N}+...+c_{1}x+c_{0}$가 주어지면 정규 분포 $\mathcal{N}(0,1)$에서 각 $c_{i}$를 sampling 함
     • $N$이 충분히 큰 경우, 해당 polynomial의 근은 unit circle로 수렴함
       - 대부분의 근은 unit circle에서 $\frac{1}{N}$ 떨어져 있고, 일부 근은 unit circle에서 $\frac{1}{N^{2}}$ 떨어져 있음
       - $2\pi \log N$개의 근은 real line에 속하며 대부분 $1$ 또는 $-1$에 가까움
       - Unit circle에 가장 가까운 실근은 $\frac{1}{N}$ 정도 떨어져 있음
     • Coefficient가 다른 분포를 가지더라도 behavior의 대부분은 변경되지 않음
       - 일반적인 condition에서 해당 polynomial의 zeros는 repulsion을 겪음
       - 따라서 polynomial과 그 derivative가 모두 작지 않다면, 근은 서로 repel 함
  2. Biquads with Normal Coefficients
     • Polynomial order $N$이 주어지면, $\mathcal{N}(0,1)$에서 independently sampling 된 $b_{j,i}$를 사용하여 $\frac{N}{2}$개의 second-order polynomials $b_{2,i}x^{2}+b_{1,i}x+b_{0,i}$를 sampling 하고 서로 multiply 함
       - 이는 근이 pair로 independently sampling 되는 과정으로, derivative polynomial의 근은 uniformly independent 하다는 것을 의미
     • $108$번의 iteration을 통한 Monte Carlo simulation에서, 해당 방법으로 sampling 된 근의 $64.8\%$는 실수로 나타남
  3. Polynomials with Uniformly Sampled Roots in the Unit Disk
     • 원하는 order $N$이 주어지면, 아래 과정을 통해 complex plane에서 $\frac{N}{2}$개 근을 sampling 함:
       1. $[0,2\pi]$에서 $\theta$ uniform을 취하고 $U \sim \mathrm{Unif}[0,1]$에서 $r = \sqrt{U}$을 취한 다음,
       2. 이후 해당 근들의 complex conjugate를 나머지 $\frac{N}{2}$ 근으로 선택
     • Derivative polynomial의 근은 uniformly independent 하고, 해당 sampling에서 실수 근의 density는 존재하지 않음
  4. Polynomials with Roots Sampled Uniformly in Magnitude and Argument
     • Polynomial order $N$이 주어지면, 아래 과정을 통해 complex plane에서 $\frac{N}{2}$개 근을 sampling 함:
       1. $[0,2\pi]$에서 $\theta$ uniform을 취하고 $[0,1]$에서 $r$ uniform을 취함
       2. 이후 해당 근들의 complex conjugate를 나머지 $\frac{N}{2}$ 근으로 선택
     • 앞선 결과와 마찬가지로 derivative polynomial의 근은 uniformly independent 하고, 해당 sampling에서 실수 근의 density는 존재하지 않음
       - 대신 unit circle 보다 원점에 더 가까운 density를 보임
  5. Characteristic Polynomial of a Random Matrix
     • Polynomial order $N$이 주어지면,
       1. Element가 $\mathcal{N}(0,1)$에서 $i.i.d$로 sampling 되는 random matrix $A \in \mathbb{R}^{N\times N}$을 취하고
       2. $\frac{1}{N}$으로 rescale 된 해당 eigenvalue를 polynomial의 근으로 사용
     • 이때 해당 근들은 서로 repulsion을 보이고, eigenvalue는 다양한 분포를 위해 unit disk로 수렴됨
       - 해당 random matrix의 characteristic polynomial은 약 $\sqrt{2N/ \pi}$의 실수 근을 가짐
     • 이러한 behavior는 $E[X] = 0, E[X^{2}]=1, E[X^{3}]=0, E[X^{4}]=3$과 같이 처음 4개 moment가 Gaussian과 match 되는 radom variable family에 대해 지속됨
       - Coefficient가 equal probability를 가지고 $\{ -1, +1\}$인 경우에 대해서는 열려있음
  6. Uniform Parametric EQ
     • 원하는 ploynomial order $N$이 주어지면 하나의 low shelf section, 하나의 high shelf section, $\frac{N-4}{2}$개의 peaking filter로 구성된 parametric EQ의 parameter를 uniformly sampling 함
     • Uniformly sampled parameter에는 각 section의 corner/center frequency, gain, $Q$ factor가 포함됨

3. Model Design

• IIRNet의 목표는,
  • $[0, \frac{f_{s}}{2}]$에 걸쳐 $F$ linearly spaced frequency에서 원하는 magnitude response $X \in \mathbb{R}^{F}$를 취하는 mapping $f_{\theta}$를 학습하도록 neural network를 training 하는 것
    1. 여기서 $f_{s}$은 sample rate이고 magnitude response $\hat{X}\in \mathbb{R}^{F}$를 사용하여 $N$-th order digital IIR filter를 추정함
       - 이때 $N$은 even 하도록 fix 됨
    2. 해당 biquad cascade는 scalar gain $G \in \mathbb{R}$과 $K$ complex poles $\{ p_{0},..., p_{K-1}|p_{k}\in \mathbb{C}\}$, $K$ complex zeros $\{ z_{0},..., z_{K-1}|z_{k}\in \mathbb{C}\}$로 구성된 $K$개의 second-order section set으로 표현될 수 있음
       - 이때 $K=N/2$
    3. 결과적으로 network는 $X, \hat{X} \in \mathbb{R}^{F}$를 사용하여 $f_{\theta}(X)\rightarrow G,P,Z \rightarrow \hat{X}$의 mapping을 학습
       - 각 pole과 zero는 complex conjugate와 paired 되어 각 biquad가 실수 coefficient를 갖도록 보장함
    4. 따라서 $k$-th biquad는:
       (Eq. 5) $H_{k}(z)=\frac{1-2Re(z_{k})z^{-1}+|z_{k}|^{2}z^{-2}}{1-2Re(p_{k})z^{-1}+|p_{k}|^{2}z^{-2}}$
  • 각 second-order section에 대한 개별적인 gain 대신 system gain $G$를 추정하면 generality를 잃지 않으면서 총 parameter 수가 줄어들고, high-order training의 stability를 높일 수 있음
    1. 이때 Sigmoid function을 IIRNet의 gain 추정에 적용한 다음 $100$을 곱하는 방식으로 system gain $G \in (0, 100)$을 강제하여 stability를 확보
    2. Minimum phase filter를 보장하기 위해, 추정된 poles $p_{k}$와 zeros $z_{k}$는 아래와 같이 rescale 됨:
       (Eq. 6) $p_{k}\leftarrow \frac{(1-\epsilon)\cdot p_{k}\cdot \tanh(|p_{k}|)}{|p_{k}+\epsilon |}$, $z_{k}\leftarrow \frac{(1-\epsilon)\cdot z_{k}\cdot \tanh(|z_{k}|)}{|z_{k}+\epsilon |}$
       - 추가적인 training stability를 위해 small constant $\epsilon=10^{-8}$을 사용
  • Training 시 network는 input과 추정된 magnitude response 간의 distance를 측정하는 loss function $\mathcal{L}$을 최소화함
    - 이를 위해 $[0, \frac{f_{s}}{2}]$의 $F$개 linearly spaced frequency에 대해 추정된 log magnitude response와 log target magnitude 간의 mean squared error를 사용:
    (Eq. 7) $\mathcal{L}=\frac{1}{F}|| \log(\hat{X})-\log (X) ||_{2}^{2} $
  • 각 second-order section의 complex response는 zero-padding을 사용하여 numerator/denomiator polynomial에 대해 discrete Fourier transform을 적용하고, 그 결과를 나누어 계산됨
    - 이러한 방식은 기존의 sample-based gradient optimization과 달리 parallelized computation이 가능
  • IIRNet architecture는,
    - Hidden dimension $D$를 갖는 $2$개의 linear layer로 구성되고 layer normalization과 $\alpha = 0.2$인 LReLU가 사용됨
    - Final layer는 hidden dimension을 filter order의 function인 filter parameter 수로 projection 함
    - 이때 복소수 값의 추정은 실수부, 허수부에 대한 개별적인 추정으로 처리됨

4. Experiments

- Settings

• Dataset : IRCAM-Listen HRTF Dataset, Kalthallen Cabs, 
• Comparisons : Modified Yule-Walker method (MYW), Stochastic Gradient Descent (SGD)

- Results

• 추정된 response와 target response 간의 MSE를 비교해 보면,
  • 각각의 특정한 random filter family에 대한 training이 해당 family를 evaluate 할 때 가장 좋은 성능을 보임
  • 특히 $C,D,E$보다는 $A,B,F$ 계열에 대한 training이 real-world filter에서 우수한 성능을 달성
  • 추가적으로 모든 filter family ($G$)에 대해 training 된 IIRNet은 가장 낮은 MSE를 달성함
    

Filter Family 별 성능 비교

• SGD, MYW와 IIRNet variant들의 성능을 비교해 보면,
  • IIRNet의 size가 증가함에 따라 run-time과 accuracy가 모두 증가하는 것으로 나타남
  • 특히 IIRNet의 모든 variant들은 SGD, MYW에 비해 더 빠르고 정확함

모델 성능 비교 결과

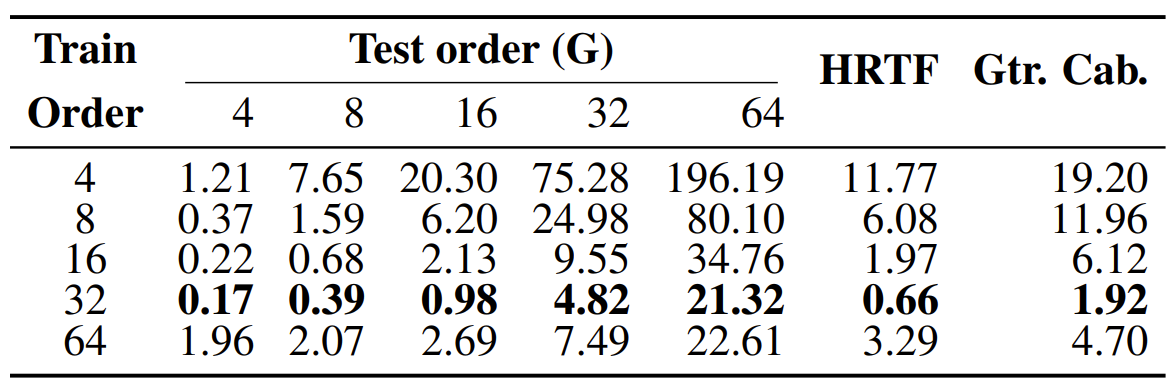
• IIRNet의 추정 filter order를 늘리면, training order 보다 작거나 같은 모든 order에서 추정 accuracy가 향상됨
  - BUT, $N \geq 64$ order의 filter를 추정하는 경우 training이 instable 하여 $32$nd order 모델보다 성능이 떨어짐

Order에 따른 IIRNet의 성능 비교