[Paper 리뷰] Sinusoidal Frequency Estimation by Gradient Descent

Sinusoidal Frequency Estimation by Gradient Descent

---

• Gradient descent를 사용하여 sinusoidal frequency parameter를 추정하는 것은 어려움
  - Error function이 non-convex 하고 local minima에 densely populated 되어 있기 때문
• Sinusoidal Frequency Estimation by Gradient Descent
  • Complex exponential surrogate의 Wirtinger derivative와 first order gradient-based optimizer를 활용
  • Differentiable signal processing을 oscillatory component의 frequency에 적용하여 joint sinusoidal frequency와 amplitude estimation을 수행
• 논문 (ICASSP 2023) : Paper Link

---

1. Introduction

• Sinusoidal parameter estimation은 signal processing에서 중요한 과정임
  • 일반적으로는 white Gaussian noise가 존재하는 sinusoidal model parameter의 Maximum Likelihood (ML)을 추정하는 방식을 사용
    - Statistical property가 잘 확립되어 있기 때문
  • 이때 sinusoidal frequency estimator는 frequency parameter의 objective function으로써 non-linearity와 non-convexity를 circumvent 해야 함
    1. 이러한 initial frequency estimate를 얻기 위해,
       - Search heuristic, spectral peak interpolation, discrete-time Fourier transform (DTFT) decorrelation과 같은 방식을 사용 가능
       - Model-based relaxtion updating, delay operator를 통한 linearizing, equivalence 한 surrogate를 활용 가능
    2. 위 방식들은 derivative-free 하고 heuristic 하기 때문에 gradient descent를 통해 fitting 되는 end-to-end model에 적용하기 어려움
       - 특히 neural network를 활용하는 Differentiable Digital Signal Processing (DDSP)에서 사용할 수 없음
  • DDSP는 harmonic-plus-noise synthesizer, audio effect control, digital synthesis control 등의 많은 digital signal processing 작업을 지원함
    - BUT, DDSP는 sinusoidal frequency estimation을 지원하지 않음
    1. Frequency domain distance에 stable 하고 informative 한 frequency gradient가 부족하기 때문
    2. Error function의 ripple로 인해 differentiable FM synthesizer의 modulation frequency를 tuning 하지 못하기 때문

-> 그래서 DDSP에서 활용 가능한 gradient descent 기반의 sinusoidal frequency estimation을 제안

 

• Sinusoidal Frequency Estimation by Gradient Descent
  • First-order gradient-based optimization이 가능한 sinusoidal oscillator에 대한 simple surrogate를 제시
  • Gradient descent를 활용하여 neural network controller에 대한 end-to-end 학습과 differentiable audio/signal processing을 지원

< Overall of This Paper >

• Complex exponential surrogate의 Wirtinger derivative와 first order gradient-based optimizer를 활용
• 결과적으로 differentiable signal processing과 gradient descent 기반의 sinusoidal estimation이 가능

2. Sinusoidal Frequency Estimation

• 다음의 discrete-time signal class를 modelling 한다고 하자
  (Eq. 1) $x_{n} = v_{n} + \sum_{k\in K}\alpha_{k} \cos(\omega_{k}n+\phi_{k})$
  - $v_{n} \sim \mathcal{N}(0, \sigma^{2})$
  - $\alpha_{k}, \omega_{k}, \phi_{k}$ : 각각 index set $K \subseteq \mathbb{N}$을 가지는 unordered sinusoidal component의 amplitude, frequency, phase parameter
  
• Standard ML deivation을 따라 추정치 $\hat{\alpha}_{k}, \hat{\omega}_{k}, \hat{\phi}_{k}$를 찾는 것은 Mean Squared Error를 최소화하는 것과 동일함
  • Audio domain에서는 Discrete Fourier Transform (DFT)와 같은 signal representation으로 likelihood를 express 함
    - 이때 $\omega_{k}$와 $\phi_{k}$가 known이면, 위의 문제는 $\alpha_{k}$에 대해 linear 함
    - $\phi$가 unknown이면, known frequency $\omega_{k}$에서 DTFT를 evaluating 하여 최적의 추정값을 얻을 수 있음
    - Frequency가 unknown인 경우는 optimization이 어려움
  • (Eq. 1)을 그대로 Mean Squared Error에 대입하면, minimization objective가 second-order intermodulation product의 sum으로 구성되기 때문에 highly non-convex 함
    - Global minimum만이 viable model fit을 나타낼 수 있기 때문에 위와 같은 loss surface는 gradient-based optimzer의 적용에 방해가 됨
    - Parameter 추정치가 해당 function의 main basin에서 initialize 되지 않으면 최적화는 잘못된 방향으로 수렴되기 때문
  • 특히 audio loss function의 gradient는 frequency에 대해 uninformative 함
    - Infinite time horizon에서 sinusoid는 orthogonal 하기 때문
  • 실제로 $N \rightarrow \infty$에 대해, 모든 $\hat{\omega}$가 $\hat{\omega} = \omega$로 loss가 0이 될 때까지 ripple이 감소함
    - 이때 $N$이 증가함에 따라, 아래 그림과 같이 informative frequency gardient가 사라져 first-order optimization이 불가능해짐
    - 반면 $N$이 너무 작으면 전체 parameter range에 걸쳐 spectral leakage가 발생하여 local minima를 만듦

두 Sinusoidal signal에 대한 Loss (a) Mean Squared Error (b) Mean Absolute Error (c) DFT Modulus Mean Squared Error

- Complex Exponential Surrogate

• 논문은 Differentialbe sinusoidal model을 위한 surrogate를 정의하여 앞선 문제를 해결함
  • Surrogate는 exponential complex number의 실수부를 통해 exponentially decaying 하는 sinusoid를 생성:
    (Eq. 2) $\mathfrak{s}_{n}(z_{k}) \triangleq \mathfrak{Re}(z_{k}^{n}) = |z_{k}|^{n} \cos n \angle z_{k}$
    - $Z = \{ z_{k} \in \mathbb{C} | k \in K \}$ : index set $K$를 가지는 specific surrogate parameter
    - $\angle z$ : $z$의 argument
    - Surrogate map $\mathfrak{s}_{n} : \mathbb{C} \rightarrow \mathbb{R}$은 complex derivative를 가지지 않음
  • 이때 partial derivative는 Wirtinger calculus를 사용하여 계산할 수 있음
    1. 따라서 $z=x+jy$에서 surrogate에 대한 conjugate Wirtinger derivative는:
       (Eq. 3) $\frac{\partial}{\partial\bar{z}}\mathfrak{s}_{n}(z) =\frac{1}{2}\left( \frac{\partial}{\partial x} + j \frac{\partial}{\partial y}\right)\mathfrak{s}_{n}(z) = \frac{n}{2}\bar{z}^{n-1}$
       - 여기서 $\mathcal{L}$을 $\mathfrak{s}$에 의해 생성된 signal과 target 사이의 loss라고 하면, $-\frac{\partial \mathcal{L}}{\partial \bar{z}}$는 steepest descent의 direction이 됨
    2. 이러한 surrogate parameter를 사용하면 signal의 frequency와 amplitude decay는 다양하게 나타남
       - 아래 그림과 같이 optimizer는 parameter를 unit circle 내부로 이동하여 exponential amplitude decay를 생성하고, real line에서 correct angle로 다시 이동할 수 있음
       
  • Minimum으로 표시되는 frequency 추정치는 surrogate parameter $\omega_{k}^{*} = \angle z_{k}^{*}$의 complex argument로 주어짐
    1. 여기서 $Z^{*} = \{ z^{*}_{k} \in \mathbb{C} | k \in K \}$는 loss를 minimize 함:
       (Eq. 4) $Z^{*} = \arg \min_{Z} \sum_{n=1}^{N}\left(x_{n}-\sum_{k\in K}\mathfrak{s}_{n}(z_{k})\right)^{2}$
    2. 이때 target amplitude $\alpha_{k} =1$이면 $|z_{k}^{*}| = 1$이고 $\angle z_{k}^{*} = w_{k}$로 frequency에 대한 ML 추정치와 동일함
    3. 한편으로 linear amplitude parameter $\hat{\alpha}_{k}$가 $\hat{\alpha}_{k}\mathfrak{s}_{n}(z_{k})$와 같이 surrogate에 도입될 수 있음
       - 이때 $\omega_{k}^{*}$은 $\alpha_{k} \neq 1$이고 $\alpha_{k}$가 known인 경우, $\hat{\alpha}_{k} = \alpha_{k}$로 둠으로써 ML 추정치를 얻을 수 있음
       - Target amplitude가 unknown인 경우, $\hat{\alpha}_{k}$는 surrogate parameter와 jointly learn 됨

Negative Wirtinger Conjugate Derivates의 Direction

• Amplitude Estimation
  • Amplitude coefficeint를 jointly learn 하는 경우에도 complex exponential surrogate와 standard sinusoid는 time에 따른 amplitude에 변화에 따라 달라질 수 있음
    - 이때 $z_{k}^{*}$을 summing 하면 least square objective를 minimize 하므로, opposite least square를 solve 함으로써 amplitude 추정치를 recover 할 수 있음
  • $|K|$ component $z_{k}$로 구성된 surrogate model에서 amplitude를 recover 하기 위해,
    1. $U \in \mathbb{R}^{N \times K}$를 정의하자
       - $u_{nk} = \cos \angle z_{k}n$, $\mathbf{v} \in \mathbb{R}^{N}$
       - 이때 $\mathbf{v} = \sum_{k=1}^{K} \mathfrak{s}_{n} (z_{k})$
    2. 어떤 linear signal representation $h : \mathbb{R}^{N} \rightarrow \mathbb{R}^{M}$에 대해, Fourier basis로의 density mapping/projection을 통한 amplitude 추정치는 ordinary least squares solution으로 주어짐:
       (Eq. 5) $\alpha^{*} = \left( H(U)^{T}H(U)^{-1}\right)^{-1}H(U)^{T}h(\mathbf{v})$
       - $H : \mathbb{R}^{N \times K} \rightarrow \mathbb{R}^{M \times K}$ : matrix의 각 column에 $h$를 적용
  • 실적용에서는 DFT의 modulus와 같은 non-linear $h$로 인해 non-linear least squares problem이 발생할 수 있음
    -> Non-linear solution이 1에 가까운 $|z_{k}^{*}|$에 대한 linear solution으로 잘 근사되는 경우, amplitude factor를 jointly learning 하고 $\hat{\alpha}_{k}\alpha_{k}^{*}$를 multipliying 하여 합리적인 추정치를 얻을 수 있음

3. Experiments

• Single Sinusoid Frequency Estimation
  • Frequency domain loss (DFT-MSE)에 대한 평균은 -83dB 이하로 떨어지지 않지만, median은 계속해서 감소함
    - Signal-Noise-Ratio (SNR)이 증가함에 따라 skewed error 분포를 나타냄을 의미
  • 결과적으로 spectrum의 modulus를 취하는 데 있어 phase information의 loss가 발생하기 때문

Single Sinusoid Frequency Estimation 결과

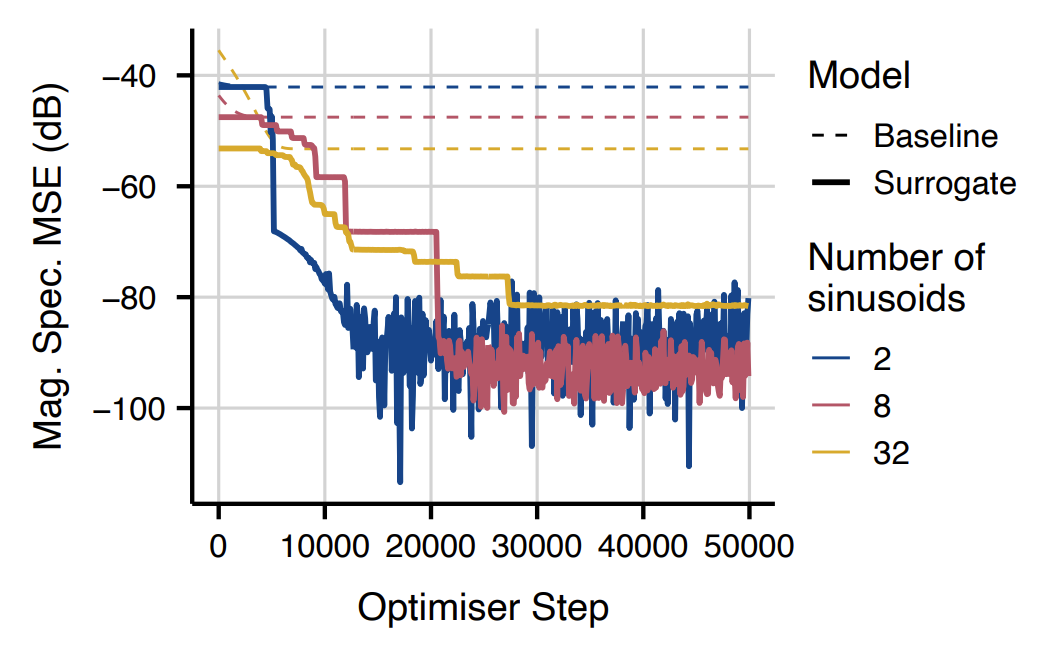
• Multi-Sinusoid Frequency and Amplitude Estimation
  • Multi-sinusoid에 대해 target과 예측 spectrum 사이의 Mean Squared Error를 비교해 보면, 제안된 surrogate는 가장 우수한 성능을 달성함
  • 이때 baeline과 random sampling의 성능은 component 수가 증가에 비례하는 경향을 보임
    - 높은 $|K|$ 값에 대해 model component와 target component 사이의 expected distance가 더 작기 때문
    - 실제로 component 수의 증가에 따라 Mean Squared Error의 감소는 $10 \log_{10} \frac{1}{4} \approx -6.02$로 나타남

Multi-Sinusoid Estimation 결과

• Surrogate의 optimization 과정을 살펴보면, surrogate가 baseline에 비해 더 크게 수렴값으로 떨어지는 것으로 나타남

Optimizer Step에 따른 Magnitude Spectra의 Mean Squared Error 변화 비교