[Paper 리뷰] Embedding a Differentiable Mel-Cepstral Synthesis Filter to a Neural Speech Synthesis System

Embedding a Differentiable Mel-Cepstral Synthesis Filter to a Neural Speech Synthesis System

---

• End-to-End controllable speech synthesis를 위해 Mel-cepstral synthesis filter를 활용할 수 있음
• Differentiable Mel-Cepstral Synthesis Filter
  • Mel-cepstral synthesis filter를 통해 voice characteristics와 pitch는 각각 frequency warping parameter와 fundamental frequency를 통해 control 될 수 있음
  • 이때 End-to-End 방식으로 최적화할 수 있도록 diffetentiable 하게 Mel-cepstral filter를 구현
• 논문 (ICASSP 2023) : Paper Link

---

1. Introduction

• Parametric speech synthesis에서는 Line Spectral Pair (LSP), Mel-cepstral filter, WORLD vocoder와 같은 linear time-variant filter가 주로 사용됨
  • 이때 Linear synthesis filter는
    - 장점 : input acoustic feature를 수정하여 voice characteristic과 pitch를 쉽게 control 가능
    - 단점 : filter의 linearity로 합성 품질이 제한되는 경향
  • WaveNet과 같은 non-linear filter는 linear filter보다 더 뛰어난 품질을 보이고 있음
    - BUT, training data에서 벗어나면 waveform 생성이 제대로 동작하지 않아 controllability가 떨어짐
    - Non-linear filter가 waveform과 acoustic feature 간의 관계를 무시하기 때문에, pitch control 측면에서 이러한 문제는 더욱 두드러짐

-> 그래서 linear/non-linear filter의 장점을 모두 활용하기 위해 Mel-cepstral filter를 speech synthesis에 도입

 

• Differentiable Mel-Cepstral Synthesis Filter
  • 기존의 Mel-cepstral filter와 동일하게 합성된 음성의 pitch와 characteristic을 쉽게 control 가능
  • Differentiable 한 구현을 통해 neural waveform 모델에서 simultaneous optimization이 가능하여 더 정확한 waveform 모델링이 가능
  • Mel-cepstral filter는 acoustic feature와 waveform 사이의 관계를 capture 할 수 있기 때문에, Generatitive Adversarial Network와 같은 복잡한 학습 전략을 필요로 하지 않음

< Overall of This Paper >

• Mel-cepstral filter를 neural network에 적용하기 위한 differentiable parallel processing의 구현
• Infinite Impulse Response filter의 recursive property를 병렬화하기 위해 Cascaded Finite Impulse Response filter를 활용
  
• 결과적으로 Mel-cepstral filter는 stacked time-variant convolution layer 형태로 공식화됨

2. Linear Synthesis System

• Linear synthesis system은,
  • Excitation signal $\mathbf{e} = [e[0], ..., e[T-1]]$와 speech signal $\mathbf{x} = [x[0], ..., x[T-1]]$ 사이에서 다음의 관계를 가정:
    (Eq. 1) $X(z) =H(z)E(z)$
    - $X(z), E(z)$ : 각각 $\mathbf{x}, \mathbf{e}$의 $z$-transform
    - 이때 Time-variant linear synthesis filter $H(z)$는 compact spectral representation으로 parameterize 됨
  • Mel-cepstral analysis에서 spectral envelope $H(z)$는 $M$-th order mel-cepstral coefficient $\{ \tilde{c}(m) \}^{M}_{m=0}$을 통해 모델링:
    (Eq. 2) $H(z) = \exp \sum_{m=0}^{M} \tilde{c} (m) \tilde{z}^{-m}$
  • 이때 first-order all-pass function $\tilde{z}^{-1}$은:
    (Eq. 3) $\tilde{z}^{-1} = \frac{z^{-1} - \alpha} {1-\alpha z^{-1}}$
    - Scalar parameter $\alpha$는 frequency warping의 intensity를 control 하므로 $\alpha$를 변경하여 $\mathbf{x}$의 voice characteristic을 수정할 수 있음
  • 따라서 (Eq. 2)를 linear synthesis filter로 사용하면 이러한 controllability를 활용 가능
• 일반적으로 mixed excitation signal은 $E(z)$로 가정됨
  • 다시 말해,
    (Eq. 4) $X(z) = H(z) \{ H_{a} (z) E_{noise}(z) + H_{p}(z) E_{pulse}(z)\}$
    - $E_{noise} (z), E_{pulse}(z)$ : 각각 white Gaussian noise와 fundamental frequency $f_{0}$에서 계산된 pulse train의 $z$-transform
  • 여기서 $H_{a} (z), H_{p}(z)$는 zero-phase linear filter로써:
    (Eq. 5) $H_{a} (z) = \cos \sum^{M_{a}}_{m=0} \tilde{c}_{a} (m) \tilde{z}^{-m}$
    (Eq. 6) $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \exp \sum^{M_{a}}_{m=-M_{a}} \tilde{c}'_{a}(m) \tilde{z}^{-m}$ 
    (Eq. 7) $H_{p} (z) = 1-H_{a}(z)$
  • 이때,
    (Eq. 8) $\tilde{c}'_{a}(m)=\left\{\begin{matrix} \tilde{c}_{a}(0), & (m=0) \\ \tilde{c}_{a}(|m|)/2, & (m \neq 0) \\ \end{matrix}\right.$
    - $\{ \tilde{c}_{a}(m) \}^{M_{a}}_{m=0}$ : aperiodicity ratio의 Mel-cepstral representation
    - Aperiodicity ratio는 각 frequency bin에 대한 $\mathbf{x}$의 aperiodic component의 intensity를 나타냄 ($[0,1]$)
  • (Eq. 4)는 $\mathbf{x}, \mathbf{e}$ 사이의 관계를 설명할 수 있지만, speech signal $\mathbf{x}$를 정확하게 모델링하는 데는 한계가 있음

3. Proposed Method

• 높은 controllability를 가지는 speech waveform을 생성하기 위해,
  • 기존의 linear synthesis filter를 다음과 같이 확장하여 waveform을 모델링:
    (Eq. 9) $X(z) = H(z) \{ P_{a} (H_{a}(z) E_{noise}(z)) + P_{p}(H_{p}(z) E_{pulse} (z))\}$
    - $P_{a}(z), P_{p}(z)$ : trainable neural network로 표현되는 non-linear filter (Prenet)
  • Mel-cepstral coefficient와 $f_{0}$를 포함한 speech component를 caputre 하기 위해 Prenet은 2개의 $Q$-dimensional latent variable vector $\mathbf{h}_{a}, \mathbf{h}_{p}$에 따라 condition 됨
    - 이때 latent variable vector $\mathbf{h}_{a}, \mathbf{h}_{p}$는 text로부터 acoustic model에 의해 jointly estimate 됨
• 모든 linear filter는 inherently differentiable 하므로,
  • 다음의 objective를 최소화함으로써 acoustic model과 Prenet을 simultaneously optimize 할 수 있음:
    (Eq. 10) $\mathcal{L} = \mathcal{L}_{feat} + \lambda \mathcal{L}_{wav}$
    - $\mathcal{L}_{feat}$ : 예측된 acoustic feature와 ground-truth feature 간의 loss
    - $\mathcal{L}_{wav}$ : 예측된 sample과 ground-truth sample 간의 loss
    - $\lambda$ : hyperparameter
  • 논문에서는 multi-resolution STFT loss를 $\mathcal{L}_{wav}$로 사용:
    (Eq. 11) $\mathcal{L}_{wav} = \frac{1}{2S}\sum_{s=1}^{S}\left( \mathcal{L}_{sc}^{(s)}(\mathbf{x},\hat{\mathbf{x}})+\mathcal{L}_{mag}^{(s)}(\mathbf{x}, \hat{\mathbf{x}})\right)$
  • 여기서,
    (Eq. 12) $\mathcal{L}^{(s)}_{sc}(\mathbf{x},\hat{\mathbf{x}}) = \frac{|| A^{(s)}(\mathbf{x})-A^{(s)}(\hat{\mathbf{x}})||_{F}}{|| A^{(s)}(\mathbf{x})||}$
    (Eq. 13) $\mathcal{L}^{(s)}_{mag}(\mathbf{x}, \hat{\mathbf{x}}) = \frac{|| \log A^{(s)}(\mathbf{x})- \log A^{(s)}(\hat{\mathbf{x}})||_{1}}{Z^{(s)}}$
    - $\hat{\mathbf{x}}$ : 예측된 speech waveform
    - $A^{(s)}(\cdot)$ : $s$-th analysis condition에서 STFT를 통해 얻은 amplitude spectrum
    - $Z^{(s)}$ : normalization term
    - $|| \cdot ||_{F}$ : Forbenius norm
    - $|| \cdot ||_{1}$ : $L_{1}$ norm
  • 학습과정에서는 $H_{p}(z)$에 제공되는 pulse train을 생성하기 위해 ground-truth fundamental frequency를 사용

Speech Synthesis System의 개요

- Differentiable Mel-Cepstral Synthesis Filter

• Differentiable Mel-cepstral filter를 구현하기 위해 (Eq. 2)를 직접 사용하는 것은 까다로움
  • Digital filter로써 exponential function이 포함되어 있기 때문
  • 따라서 논문은 Mel-Log Spectrum Approximation (MLSA) filter를 활용함
    - MLSA filter는 Pade approximation을 통해 exponential function을 lower-order rational function으로 대체하는 방식
    - 이때 MLSA filter는 recursive 하기 때문에 이전에 계산된 input signal $e[t]$가 현재의 $x[t]$를 계산하는 데 사용됨
    -> 결과적으로 recursive 특성으로 GPU 상에서 parallel processing이 어려움

• 위 문제를 해결하기 위해,
  • Linear transformation을 통해 Mel-cepstral coefficient를 cepstral coefficient로 변환:
    (Eq. 14) $H(z) \simeq \exp \sum_{m=0}^{N}c(m)z^{-m}$
    - $\{ c(m) \}_{m=0}^{N}$ : $\{ \tilde{c}(m) \}_{m=0}^{M}$에서 계산된 $N$-th order cepstral coefficient
  • 이후 (Eq. 14)의 exponential function에 대해 Maclaurin expansion을 취하면:
    (Eq. 15) $H(z) \simeq \sum_{\ell =0}^{L}\frac{1}{\ell!}\left( \sum_{m=0}^{N}c(m) z^{-m}\right)$
    - Infinite series는 $L$-th term에 의해 truncate 됨
  • (Eq. 15)는 Mel-cepstral synthesis filter가 $L$-stage Finite Impulse Response (FIR) filter로 구현될 수 있음을 의미
    - 결과적으로 추정된 Mel-cepstral coefficient로부터 weight가 dynamically compute 되는 $L$개의 time-variant convolution layer로 구성됨

Mel-Cepstral Synthesis Filter

3. Experiments

- Settings

• Dataset : Japanese corpus dataset (Internal)
• Comparisons
  1. MS-sg : Prenet $P_{a}, P_{p}$는 사용하지 않고 (Eq. 15)의 Mel-cepstral filter를 통해 waveform을 합성
     - sg는 stop gradient, $\mathcal{L}_{feat}$만을 사용하여 학습
     
  2. MS : $\mathcal{L}_{feat}, \mathcal{L}_{wav}$ 2개의 loss를 활용한 MS-sg
  3. PMS-sg : (Eq. 10)의 Prenet을 적용하여 acoustic model과 simulatenously train 한 모델
     - 이때 $\mathcal{L}_{wav}$는 $\mathbf{h}_{a},\mathbf{h}_{p}$만을 통해 acoustic model에 전달됨
     - 결과적으로 Mel-cepstral coefficient는 $\mathcal{L}_{wav}$에 영향을 받지 않음
  4. PMS : (Eq. 10)을 통해 Prenet, acoustic model을 ssimulatenously traing 한 모델
  5. PN-sg : $\mathcal{L}_{feat}$만으로 학습된 모델
     - Mel-cepstral filter를 적용하지 않고 PeriodNet을 사용하여 waveform을 합성

- Results

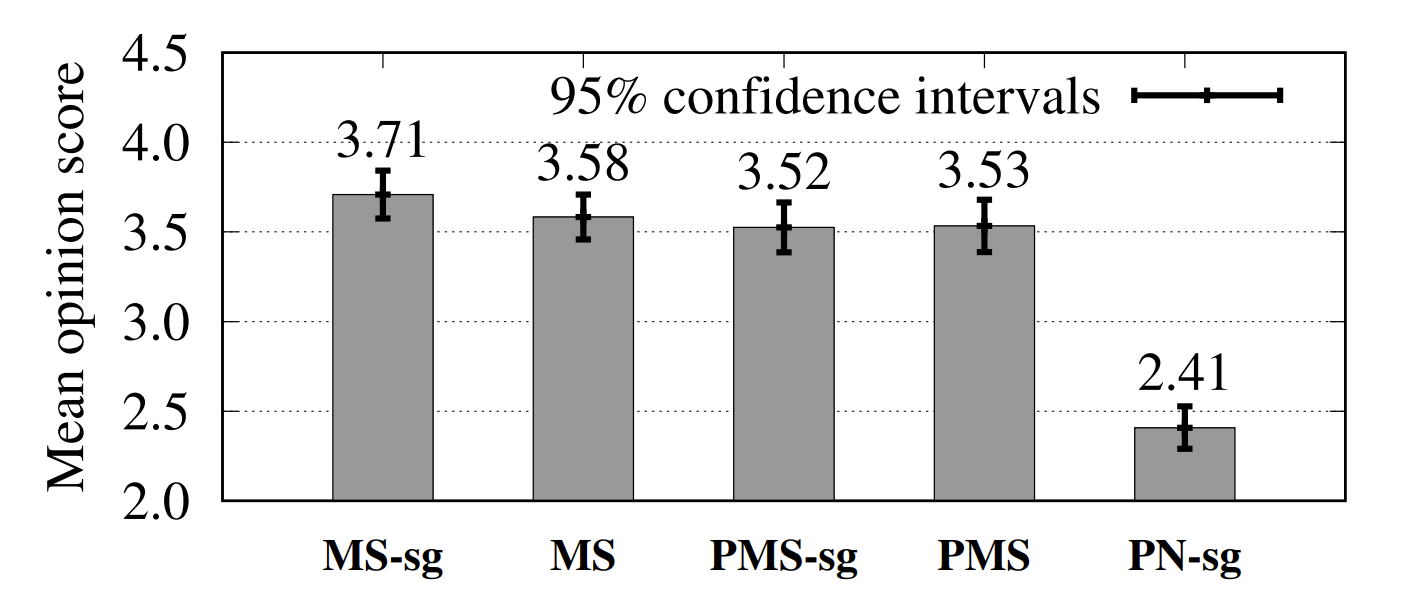
• MOS 측면에서 MS는 MS-sg보다 더 높은 결과를 보임
  • 결과적으로 waveform domain의 loss를 고려하는 것이 음성 품질 향상에 도움을 줄 수 있음
  • 특히 PMS는 MS 보다 더 나은 성능을 보였는데, 이는 Prenet이 linear filter를 보완할 수 있음을 의미

MOS 비교 결과

• Fundamental frequency를 12 semitone으로 shift 한 경우 각 합성 품질을 비교했을 때,
  - 순수한 neural waveform 모델인 PN-sg는 PMS, MS에 비해 robustness가 떨어지는 것으로 나타남

Fundamental Frequency를 shift 했을 때 MOS 비교 결과

• Prenet이 사용된 excitation signal과 사용되지 않은 excitation signal을 비교해 보면,
  - Prenet은 Mel-cepstral coefficient가 잘 caputre 할 수 없는 높은 frequency domain에서 동작하는 것으로 나타남

Excitation Signal 비교 (좌) w/o prenet (우) w/ prenet