[Paper 리뷰] Differentiable Signal Processing with Black-Box Audio Effects

Differentiable Signal Processing with Black-Box Audio Effects

---

• Audio effect를 deep neural network로 통합하여 automate audio signal processing을 수행할 수 있음
• DeepAFx
  • Non-differentiable black-box effect layer를 학습시키기 위해 stochastic gradient approximation을 활용하여 end-to-end backpropagation을 생성
  • Tube amplifier emulation, automatic mastering, breath removal에 대한 audio production 작업에 적용 가능
• 논문 (ICASSP 2021) : Paper Link

---

1. Introduction

• Audio signal processing effect (Fx)는 loudness, dynamics, frequency, timbre 등의 sound characteristics를 다루는 데 사용됨
  • 대부분의 Fx는 사용하기 어렵고 원하는 task에 대해 powerful하지 않아 한계가 있음
    - 이를 해결하기 위해 circuit modeling, analytical method, intelligent audio effect 등을 활용할 수 있음
    - Intelligent audio effect는 sound engineering best practice를 통해 parameter setting을 dynamic 하게 변경하는 방식
    - 이를 위해서는 기존 processor의 automation을 통한 adaptive signal processing system을 필요로 함
  • Audio effect modeling을 위해 deep learning method를 활용할 수 있음
    1. Neural proxy가 audio effect transformation을 학습하고 적용하는 end-to-end direct transformation
       - 각 effect 마다 특수한 custom modeling을 필요로하고, editable parameter control이 제한적임
    2. DNN이 audio effect의 parameter setting을 예측하는 parameter estimator
       - Input, control parameter, target output에 대한 대량의 human-labeled data가 필요함
    3. Differentiable Digital Signal Processing (DDSP)와 같은 auto-differentiation framework
       - Fx로의 re-implementation을 위한 추가적인 작업이 필요

-> 그래서 deep neural network에서 arbitary stateful, third-part black-box processing effect를 사용할 수 있는 DeepAFx를 제안

 

• DeepAFx
  • 기존의 deep learning operator와 black-box effect를 mix-and-match 하여 사용가능
    - Neural proxy, Fx re-implementation 없이도 intelligent audio effect task를 처리 가능
  • 이를 위해,
    1. Encoder가 input audio를 분석하고 Fx black-box control을 학습하는 deep architecture를 구현
    2. Stochastic gradient approximation을 활용하여 non-differentiable black-box audio effect layer에서 end-to-end backpropagation을 허용
    3. Stateful black-box processor를 지원하는 training shceme
    4. Effects layer group delay에 대해 robust한 delay-invariant loss의 도입
  • Tube amplifier emulation, automatic non-speech sound removal, automatic music mastering 과정에 적용
    - 결과적으로 automatic audio production을 지원하고, 고품질의 mastering이 가능

< Overall of DeepAFx >

• Non-differentiable black-box effect layer를 학습시키기 위해 stochastic gradient approximation을 도입
• End-to-end backpropagation을 가능하게 하고 stateful black-box processing effect를 지원
• Tube amplifier emulation, automatic mastering, breath removal에 대한 audio production 작업에 적용 가능

2. Method

- Architecture

• DeepAFx는 두 부분으로 구성됨
  1. Deep encoder
     - Input audio를 분석하고 audio effect에 제공되는 parameter를 예측
  2. 1개 이상의 audio effect로 구성된 black-box layer
• Deep Encoder
  • Audio representation을 학습하기 위한 deep architecture
  • Long temporal dependency를 학습하기 위해 input $\tilde{x}$는,
    - Previous/subsequent context sample을 포함하는 large audio frame 중심에 위치한 current audio frame $x$을 활용
  • 구조적으로,
    - Encoder input은 log-scaled mel-spectrogram non-trainable layer와 batch normalization으로 구성됨
    - Encoder의 마지막 layer는 $P$ unit의 dense layer와 Sigmoid activation으로 구성됨
    - $P$ : 총 parameter 개수
  • Encoder output은 current input frame $x$에 대해 예측된 parameter $\hat{\theta}$
• Audio Fx layer
  • 1개 이상의 connected audio effect로 구성된 stateful black-box
  • Input audio $x$와 parameter $\hat{\theta}$를 사용하여 output waveform $\bar{y} = f(x,\hat{\theta})$를 생성
    - 이때 transformed audio와 target audio 간의 loss를 적용 

Overall of DeepAFx

- Gradient Approximation

• Backpropagation을 통해 DeepAFx를 학습시키기 위해, audio Fx layer, deep encoder에 대한 loss function의 gradient를 계산
  • Deep encoder의 경우 standard automatic differentiation을 활용할 수 있지만, audio Fx layer는 non-differentiable 함
    - Audio Fx layer에 대한 gradient approximation을 위해 Finite Difference (FD), evolution strategy, reinfocement learning, neural proxy 등을 활용할 수 있음
    - 논문은 stochastic gradient approximation인 Simultaneous Permutation Stochastic Approximation (SPSA)를 채택
  • 이후 공식화를 위해 input signal $x$의 gradient를 무시하고 parameter의 gradient만 approximate
• FD
  • FD는 current parameter set $\hat{\theta}_{0}$에서 audio Fx layer의 gradient를 approximate 하기 위해 사용될 수 있음
  • 이때 gradient $\tilde{\nabla}$는 $\tilde{\nabla}f(\hat{\theta}_{0})_{i} = \partial f(\hat{\theta}_{0})/\partial \theta_{i}, \,\, i=1,...,P$로 characterize 되는 partial derivative로 정의될 수 있음
  • Two-side FD approximation $\tilde{\nabla}^{FD}$는,
    1. Constant $\epsilon$으로 perturb 된 $f()$에 대한 backward, forward measurement를 기반으로 함
    2. 이때 $\tilde{\nabla}^{FD}$의 $i$-th component는:
       (Eq. 1)  $\tilde{\nabla}^{FD}f(\hat{\theta}_{0})_{i} = \frac{f(\hat{\theta}_{0}+\epsilon \hat{d}^{P}_{i}) - f(\hat{\theta}_{0}-\epsilon \hat{d}^{P}_{i})}{2\epsilon}$
       - $0 < \epsilon \ll 1$, $\hat{d}^{P}_{i}$ : $P$-dimension과 $i$-th place에 1을 가지는 standard basis vector
  • (Eq. 1)로부터 각 parameter $\theta_{i}$는, 한 번에 하나씩 perturb 되기 때문에 $2P$ function evaluation이 필요함 
    - 따라서 만약 $f()$가 1개 이상의 audio effect를 나타내는 경우, 작은 $P$에 대해서도 많은 계산 비용이 요구됨
    - 특히 $f()$가 stateful 하면 FD perturbation은 $f()$에 대한 $2P$ instantiation을 필요로 하므로 memory 사용량이 증가함

• SPSA
  • SPSA는 FD의 단점을 해결할 수 있는 multivariate system에 대한 stochastic optimization 방법
    - Gradient approximation을 위해 gradient descent 기반의 최적화를 사용
  • SPSA gradient estimator $\tilde{\nabla}^{SPSA}$는 모든 parameter $\hat{\theta}$의 random perturbation을 기반으로 함
    1. 이때 $\tilde{\nabla}^{SPSA}$의 $i$-th element는:
       (Eq. 2) $\tilde{\nabla}^{SPSA}f(\hat{\theta}_{0})_{i} = \frac{f(\hat{\theta}_{0}+\epsilon \hat{\Delta}^{P})-f(\hat{\theta}_{0}-\epsilon \hat{\Delta}^{P})}{2\epsilon \Delta_{i}^{P}}$ 
       - $\hat{\Delta}^{P}$ : symmetric Bernoulli 분포에서 sampling 된 $P$-dimensional random perturbation vector
       - 즉, 확률 0.5에 대해 $\Delta_{i}^{P} = \pm 1$
    2. 각 iteration에서 $f()$의 총 function evaluation 횟수는 2
       - (Eq. 2)의 numerator가 $\tilde{\nabla}^{SPSA}$의 모든 element에 대해 identical 하기 때문
       - 따라서 SPSA는 $P$가 크거나 $f()$가 stateful 하더라도 FD 보다 효율적임

- Training with Stateful Black-Boxes

• Training sample은 일반적으로 independent identically distributed (i.i.d.) 조건을 따라야 하지만 audio effect는 stateful system임
  • Output sample은 previous input sample이나 internal state에 의존적이라는 것을 의미하므로
    - DeepAFx 학습 과정에서 audio Fx layer에 i.i.d.-sampled audio를 공급하면 state를 손상시켜 비현실적인 output을 생성하게 됨
  • 이를 해결하기 위해,
    - $N$ size의 consecutive non-overlapping frame을 audio Fx layer에 공급 ($N$ hop size의 audio frame)
    - 이때 각 audio effect의 internal block size는 $N$의 divisor로 설정됨
• Mini-batch를 활용하기 위해 batch의 각 item에 대해 별도의 Fx processor를 사용
  • 따라서 batch size $M$에 대해 backpropagation의 forward pass를 위한 $M$개의 independent audio effect를 instantiate 함
    - 각각의 $M$개 plugin은 random audio clip에서 training sample을 얻고
    - Mini-batch 전반에 걸쳐 각 instance는 새로운 sample로 swap 될 때까지 동일한 input에서 sample을 받음
  • SPSA의 two-side function evaluation을 위해 batch item 당 2개의 additional Fx를 사용하여 stateful constraint를 충족시킴
    - 이를 통해 SPSA를 graident로 최적화하기 위해 $3M$의 audio effect만을 요구함
    - 그에 비해 FD는 parameter 수 $P$, batch size $M$에 대해 $(2P+1)M$의 unmanageable effect가 필요
    
  • 최종적으로 mini-batch의 item에 대한 gradient operator를 병렬화함
    - Distributed training과 비슷하게 single one-GPU, multi-GPU setup을 활용

- Delay-Invariant Loss

• Multi-band audio effect는 다양한 filter를 통해 input signal을 다양한 frequency band로 split 하는 audio processor
  • 해당 filter를 통해 input의 sinusoidal component의 frequency-dependent time delay인 group delay를 반영할 수 있음
    - 이를 통해 $180^{\circ}$ phase shift와 같은 input sign invert를 수행할 수 있음
    - BUT, Fx가 동작할 때 time, frequency domain에 대한 inexact input으로 인해 loss function의 적용이 어려울 수 있음
  • 따라서 delay-invariant loss function을 도입하여 해당 문제를 해결
    1. 먼저 cross-correlation $\star$를 통해 output $\bar{y}$와 target $y$ audio frame 간의 time delay $\tau = argmax(\bar{y} \star y)$를 계산
    2. 이때 time-domain loss는:
       (Eq. 3) $L_{time} = \min (|| \bar{y}_{\tau}-y_{\tau}||_{1}, ||\bar{y}_{\tau}+y_{\tau}||_{1})$
       - Time-aligned target $y_{\tau}$와 $0^{\circ}$, $180^{\circ}$ phase shift time-aligned output $\bar{y}_{\tau}$간의 $L1$ distance의 최값을 의미
    3. 이후 $Y_{\tau}, \bar{Y}_{\tau}$를 $y_{\tau}, \bar{y}_{\tau}$에 대한 1024-point FFT로 계산하고, frequency-domain loss $L_{freq}$를 다음과 같이 정의:
       (Eq. 4) $L_{freq} = ||\bar{Y}_{\tau}-Y_{\tau}||_{2}+|| \log \bar{Y}_{\tau}-\log Y_{\tau}||_{2}$
       
    4. 따라서 최종 loss function은:
       $L = \alpha_{1}L_{time} +\alpha_{2}L_{freq}$
       - 논문에서는 $\alpha_{1} =10, \alpha_{2} =1$로 설정

3. Experiments

- Settings

• Dataset :
  - Tube amplifier emulation : IDMT-SMT-Audio-Effects dataset
  - Automatic non-speech sound removal : DAPS dataset
  - Automatic music mastering : 'Mixing Secrets' Free Multitrack Download Library
• Encoder variants : Inception, MobileNet v2
• Comparisons : Convolutional Audio Effects Modeling Network (CAFx), Online Mastering Software (OMS)

- Results

• Qualitative Evaluation
  • Tube amplifier emulation에서는
    - DeepAFx로 예측된 spectrogram은 analog target과 유사하게 emulate 되어 나타남
    - 특히 multi-band compressor parameter는 guitar note의 attack, decay에 대해 시간이 지남에 따라 이동하며 tube amplifier의 non-linear hysteresis behavior를 emulate 함
  • Non-speech sound removal의 경우
    - DeepAFx는 breath와 lip smacking sound를 성공적으로 제거함
    
  • Music mastering의 경우
    - DeepAFx의 결과는 sound engineer의 mastering target과 match 되는 것으로 나타남
    - Unmastered music track에 대해 3가지 audio effect가 점진적으로 변화됨

Input, Target, Predicted Spectrogram 비교 (좌) Tube amplifier emulation (중) Non-speech sound removal (우) Music mastering

• Quantative Evaluation
  • MFCC cosine distance $\tilde{d}_{MFCC}$를 기준으로 정량적인 평가를 수행
  • DeepAFx의 encoder로써 Inception을 사용하는 것이 MobileNet v2 보다 조금 더 좋은 성능을 보임

MFCC cosine distance 기반 정량적 품질 평가

• Perceptual Evaluation
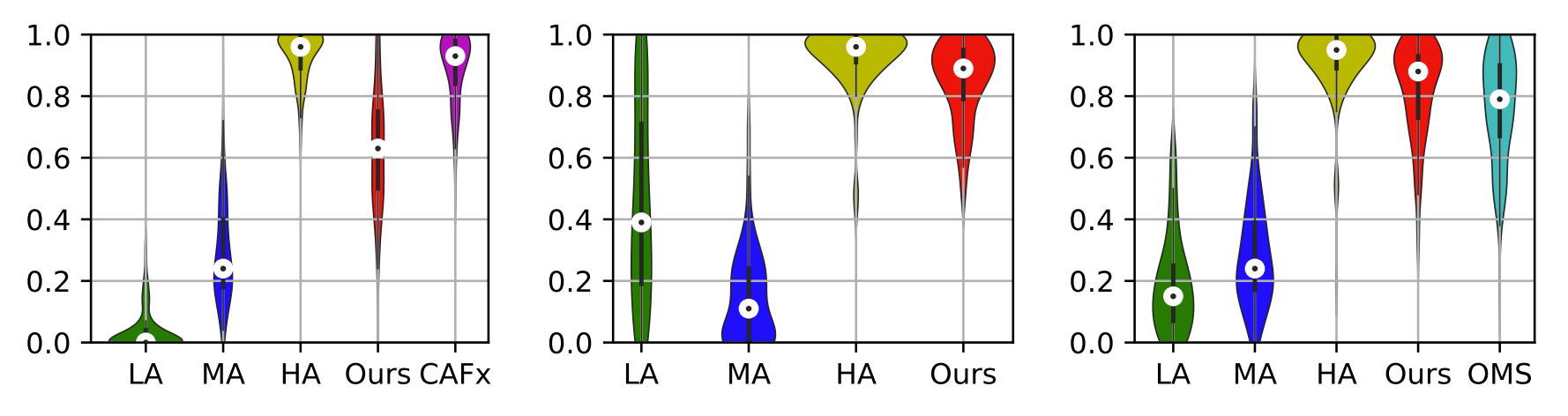
  • Listening test에 대한 Violin plot을 비교
  • Amplifier emulation의 경우, DeepAFx는 복잡한 neural proxy를 사용하지 않고도 emulation에 특화된 CAFx와 비교할만한 성능을 발휘
  • Non-speech sound removal에서는 DeepAFx가 hidden anchor (HA) 수준의 높은 결과를 얻음
  • Music mastering에서는 DeepAFx가 OMS 보다 더 지각적으로 우수하다는 것으로 나타남 

Listenting test에 대한 Violin Plot (좌) Tube amplifier emulation (중) Non-speech sound removal (우) Music mastering