[Paper 리뷰] Lightweight and Interpretable Neural Modeling of an Audio Distortion Effect Using Hyperconditioned Differentiable Biquads

Lightweight and Interpretable Neural Modeling of an Audio Distortion Effect Using Hyperconditioned Differentiable Biquads

---

• Audio distortion effect를 모델링하기 위해 differentiable cacaded biquads를 사용할 수 있음
• Hyperconditioned Differentiable Biquads
  • Trainable Infinite Impulse Response (IIR) filter를 hyperconditioned case로 확장
  • Transformation은 distortion effect의 external parameter를 internal filter와 gain parameter에 직접 mapping 하고 filter stability를 보장하는 activation을 학습
  • Fourier transform을 통해 IIR filter에 대한 효율적인 training scheme을 제시
• 논문 (ICASSP 2021) : Paper Link

---

1. Introduction

• Analog audio circuit의 digital emulation을 통해 audio effect를 광범위하게 사용할 수 있음
  • Wave digital filter와 같은 virtual analog technique은 high-fidelity emulation을 제공할 수 있지만, expensive한 online solver가 필요함
  • Deep neural network의 등장으로 audio effect를 data-driven 방식으로 모델링하는 것이 가능해짐
    - WaveNet에 대한 여러 variant는 tube amp emulating이나 distortion pedal에서 우수한 성능을 보임
    - 이를 통해 underlying effect의 external parameter를 효과적으로 모델링 할 수 있지만, 여전히 complexity가 높고 black-box 구조로 인해 interpretability가 떨어짐
  • 한편으로 differentiable audio processor를 구현하는 방법도 있음
    - 대표적으로 Infinite Impulse Response (IIR) filter를 통해 audio effect에 적용할 수 있음
    - BUT, IIR filter는 external parameter를 모델링하기 어렵고 특히 recurrent layer 형태로 구현할 경우, 학습할 수 있는 filter 수가 제한되어 applicability가 저하됨

-> 그래서 differentiable audio distortion effect 모델링을 위해 multiple differentiable biquad를 활용하는 방식을 제안

 

• Hyperconditioned Differentiable Biquads
  • IIR filter를 building block으로 사용하여 lightweight, interpretable audio effect 모델링을 지원
  • User-facing parameter를 기반으로 filtering stage의 변화를 capture하는 Hyperconditioning (HC)을 채택
    - 기존의 deep learning을 통한 trainable IIR filter 방식에서 탈피
  • 다양한 Cascaded Biquad (CB) representation을 고려하고 안정적인 학습을 위한 activation function을 제시
  • Tractable 한 frequency-domain sampling을 지원하는 training scheme을 적용

< Overall of This Paper >

• IIR filter를 hyperconditioned case로 확장하여 distortion effect의 external parameter를 internal filter와 gain parameter에 직접 mapping 하고 filter stability를 보장
• Fourier transform을 통해 IIR filter에 대한 효율적인 training scheme을 제시
• 결과적으로 기존 black-box 모델에 비해 더 lightweight하고 interpretable 한 성능을 발휘

2. Background Information

• Biquad (2nd order IIR filter)는,
  • 다음의 difference equation을 가짐:
    (Eq. 1) $y[n]=b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]-a_{1}y[n-1]-a_{2}y[n-2]$
    - $\mathbf{b} = [b_{0}, b_{1}, b_{2}]$ : filter의 feedforward gain, $\mathbf{a}=[1,a_{1},a_{2}]$: filter의 feedback gain
  • 실수 $\mathbf{b}, \mathbf{a}$에 대해, biquad의 transfer function은:
    (Eq. 2) $H(z)=\frac{b_{0}+b_{1}z^{-1}+b_{2}z^{-2}}{1+a_{1}z^{-1}+a_{2}z^{-2}} = b_{0}\frac{(z-q_{0})(z-q_{1})}{(z-p_{0})(z-p_{1})}$
    - Zeros의 pair $\{ q_{0}, q_{1} \}$과 poles의 pair $\{p_{0},p_{1}\}$은 filtering의 nature를 나타내고 $b_{0}$는 gain을 control
    - $|p_{0}| <1, |p_{1}|<1$일 때, $a_{1}, a_{2}$가 biquad triangle 내부에 있도록 constraint 되면 stability가 보장됨
  • Biquad의 frequency response는 $e^{j\omega}$를 argument로 사용하여 (Eq. 2)를 evaluating 함으로써 linearly-spaced digital frequency $\omega$의 vector에 대해 evaluate 할 수 있음
  • 이때 high order IIR filter는 $K$ biquad를 cascade 하여 생성되고, 해당 cascade의 composite complex frequency response는:
    (Eq. 3) $H_{\textrm{cascade}}(e^{j\omega}) = \prod_{k=0}^{K-1}H_{k}(e^{j\omega})$
    - 이를 cascaded freqz operation이라고 함
  • Biquad는 arbitrary 2nd order filter를 모델링 하지만 RBJ cookbook은,
    - 주어진 sampling rate $f_{SR}$에서 specified center/cutoff frequency $f$ (Hz), gain $g$ (dB), $Q$/slope $Q$를 사용하여 parameteric peaking과 shelving filter에 대한 explicit formula를 정의
    - 이러한 filter parameterization을 통해 interpretable 하고 stable 한 design을 지원 가능

Filter Stability를 보장하는 Biquad Triangle

3. Modeling Using Differentiable Biquads

• Proposed method에서
  • Input audio $\mathbf{x}$는 parametric delay layer를 거쳐 $\mathbf{y}_{-1}$을 생성한 다음, $S$개의 filtering stage를 통과
  • 각 filtering stage $s$는 $K$개 biquad의 cascade, multiplicative gain $\alpha_{s}$, tanh non-linearity (NL)로 구성됨
    - 최종 stage에서는 NL이 생략됨
    - 각 biquad는 $P$ filter parameter로 표현되고, 사용되는 specific representation에 따라 달라짐
  • Previous stage $\mathbf{y}_{s-1}$의 audio signal 외에도 각 filtering stage는 사용자로부터 input $C_{s}$의 external parameter를 취함
    - 이를 통해 filtering stage의 underlying parameter를 altering 할 수 있는 conditioning vector $\mathbf{c}_{s}$를 생성
    - Vector $\mathbf{c}_{s}$는 parameter automation을 위해 time에 따라 변하도록 구성
  • 최종 stage의 $\mathbf{y} = \mathbf{y}_{S-1}$의 output은 모델링한 effect의 ground-truth output에 대한 추정치가 됨

Proposed Architecture

- Parametric Delay Layer

• Input은 delay (non-integer sample)와 linear gain, 2개의 trainable parameter로 parameterize 된 delay layer를 통해 전달됨
  • Delay layer는 dataset의 input과 output 사이의 potential timing offset을 accommodate 함
  • Delay parameter는 합이 1이 되는 2개의 tap으로 구성된 linear fractional delay filter에 mapping 됨
    - 이때 delay filter 계산은 generic sinc interpolation kernel이나 non-sparse convolution을 사용할 수 있지만, complexity의 문제가 있음
  • 따라서 논문에서는 filtered result에 linear gain term을 multiply 하는 방식을 사용
    - 이를 통해 network에 signal을 potentially invert 할 수 있는 능력을 제공 가능
    - 여기서 각 block에 사용된 tanh NL은 symmetric 하므로, odd number의 inverting amplifier stage를 포함하는 circuit을 충분히 모델링할 수 있음

- Hyperconditioned Blocks

• 일반적으로 IIR filter는 fixed filter를 통해 학습되거나 addition, concatenation, adpative instance normalization과 같은 방식으로 주어지는 conditioning information을 활용함
  • 이와 달리 Hyperconditioning (HC)는 underlying model weight를 ultimately control 하는 conditioning signal의 transformation을 학습함
    - 따라서 HC를 사용하면 보다 expressive 한 audio style transfer가 가능
  • Biquad cascade에 HC를 도입하고 filtering stage에서 gain을 적용하여 conditioning information을 모델에 inject
    - i.e) $[0,1]$ range 내에 있도록 scale 된 user-facing effect parameter
    - 결과적으로 $1\times 1$ convolution으로 구현된 single affine transformation을 통해 filtering stage $s$에서 conditioning vector $\mathbf{c}_{s}$를 underlying parameter로 transform
• 이때 모델링되는 circuit의 schematic을 inspection 하면 적절한 $S, K$ 값과 external parameter를 결정할 수 있음
  • Conditioning site에 대한 knowledge를 inject 하면 parameter size 수를 더욱 줄이고, inductive bias를 impose 함
  • $C_{s} >0$인 block의 경우, HC network를 사용하여 conditioning signal을 해당 parameter 수로 변환
  • 그 외의 경우, fixed gain을 학습하고 stage에 대한 filtering을 수행하는 trainable weight를 사용

- Cascaded Biquad Representations

• Fixed IIR filter를 학습할 때 적절한 initialization은 filter stability를 보장할 수 있지만, user input에 따라 변화하는 hyperconditioned filter에는 적합하지 않음
  • 따라서 parameter에 stability constraint를 impose 하는 representation-specific activation을 통해 stable training을 보장
  • 이러한 activation을 p2c라고 하고, parameter를 최종 filter coefficient와 gain에 mapping 하기 위해 수행되는 모든 operation을 characterize 함
    
• Cascaded Biquad (CB)의 다음 3가지 parameterization을 고려
  1. Coefficient Representation
     • 1st parameterization에서는 coefficient vector $\mathbf{b}_{s,k}, \mathbf{a}_{s,k}$를 사용하여 stage $s$의 $k$-th biquad를 characterize
     • 각 CB 다음에는 gain이 따르므로, 모델 expression에 큰 loss가 없는 모든 filter에 대해 $b_{0,s,k}=1$로 설정
       - Filter parameter의 vector $\mathbf{v}_{s,k} = [b_{1,s,k},b_{2,s,k},a_{1,s,k},a_{2,s,k}]$이고 $P=4$
       - 이때 stability를 위해서 $a_{1,s,k}, a_{2,s,k}$는 biquad triangle 내부에 존재해야 함
     • 이는 아래의 activation을 수행하는 것으로 해결됨:
       (Eq. 4) $a_{1,s,k}\leftarrow 2\cdot \tanh a_{1,s,k}$
       (Eq. 5) $a_{2,s,k}\leftarrow [(2-|a_{1,s,k}|) \tanh a_{2,s,k}+|a_{1,s,k}|]/2$
  2. Pole / Zero Representation
     • 2nd parameterization은 각 biquad를 single pole과 zero의 실수, 허수부로 characterize 하고 나머지 pole과 zero는 complex conjugate가 되도록 constraint 함
       - 이때 $\mathbf{v}_{s,k}=[\mathfrak{R}\{q_{s,k}\},\mathfrak{I}\{q_{s,k}\}, \mathfrak{R}\{p_{s,k}\},\mathfrak{I}\{p_{s,k}\}]$이고, $P=4$
       
     • Stability는 아래의 activation을 사용하여 $|p_{s,k}|<1$로 contraining 함으로써 보장됨:
       (Eq. 6) $p_{s,k}\leftarrow p_{s,k}\tanh (|p_{s,k}|)/|p_{s,k}|$
       - $\mathbf{b}_{s,k} =[1,-2\mathfrak{R}\{q_{s,k}\},\mathfrak{R}\{q_{s,k}\}^{2}+\mathfrak{I}\{q_{s,k}\}^{2}]$
       - $\mathbf{a}_{s,k}=[1,-2\mathfrak{R}\{p_{s,k}\},\mathfrak{R}\{p_{s,k}\}^{2}+\mathfrak{I}\{p_{s,k}\}^{2}] $
  3. Parametric EQ Representation
     • Final parameterization에서는 parametric equalizer (EQ)를 사용하여 각 CB를 모델링함
       - 각 parametric EQ는 low shelf, high shelf, $K-2$ peaking filter로 구성
       - 이때 $\mathbf{v}_{s,k} =[f_{s,k},g_{s,k},Q_{s,k}]$이고, $P=3$
       - Parametric EQ parameter는 RBJ cookbook formula를 통해 biquad filter coefficeint로 convert 됨
     • $f_{s,k}$에 대한 activation을 $[0,f_{SR}/2]$, $f_{s,0} \leq f_{s,1} \leq ... \leq f_{s,K-1}$에 속하도록 정의하면:
       (Eq. 7) $f_{s,k}\leftarrow (f_{SR}/K)\sum_{k=0}^{K-1}| \lfloor f_{s,k} \rceil - f_{s,k}|$
       - $\lfloor \cdot \rceil$ : round operator
       - dB-specified gain은 RBJ cookbook에서 linear scale로 convert 되지만, $g_{s,k}$에는 activation이 적용되지 않음
     • 이때 $Q_{s,k}$는 non-negative이고 shelving filter의 어떤 경우에 대해서도 $\leq 1$이어야 함
       - 따라서 $Q_{s,k}$의 activation은:
       (Eq. 8) $Q_{s,k}\leftarrow Q_{\max,k}\cdot \sigma(Q_{s,k})$
       - 여기서 $\sigma(\xi)=1/(1+e^{-\xi})$이고,
       (Eq. 9) $Q_{\max, k} = \left\{\begin{matrix}
       3, & \textrm{if}\,\,\, 0<k<K-1 \\
       1, & \textrm{otherwise} \\
       \end{matrix}\right.$
     • 해당 parameterization은 다른 representation보다 degree of freedom이 하나 적지만, 더 interpretable 함

- Implementation and Training

• Recurrent layer를 사용하여 differentiable IIR filter를 구현할 수 있음
  • BUT, cascade 하려는 filter의 수와 해당 layer가 $f_{SR} \geq 44.1 \textrm{kHz}$의 audio sample에서 동작한다는 점을 고려하면 recurrent 방식은 매우 느림
  • 따라서 differentiable operation을 사용하여 각 represenation에 대해 (Eq. 3)와 p2c procedure의 cascaded freqz computation을 구현하여 differentiable biquad training을 수행
    1. 이때 underlying $N$-point Fast Fourier Transform (FFT)의 frequency axis와 일치하도록 $\omega$를 설정하면 frequency-domain에서 filtering을 수행할 수 있음
       - $N$이 충분히 크다면, system response의 frequency-domain sampling으로 발생하는 time-aliasing 양은 실제 IIR response와 근사할 정도로 작음
    2. 해당 방식은 parametric EQ matching을 위해 처음 도입되었음
       - 논문에서는 이를 기존의 time-domain audio effect 모델링 보다 general 한 문제로 확장
  • 결과적으로 short-time Fourier transofrm을 통해 arbitrary length signal을 학습할 수 있음
    - 추론 시, filtering stage parameter는 input parameter setting에서 추론되고, resulting filter는 reculsive 하게 구현됨

- Model Complexity and Interpretability

• 제안된 모델의 parameter 수는: $2+\sum_{s=0}^{S-1}(1+KP)(1+C_{s})$
  • Interpretability가 부족한 neural network와는 달리 제안된 방식은 transparent 하고 intuitive 함
    - 특히 parametric equalizer representation을 사용하면 학습 이후, 모델의 각 stage를 hand-tuning 할 수 있음
  • HC affine transformation의 bias는 user input이 0으로 설정된 stage의 'quiescent' state에 해당
    - 따라서 hyperconditioned filtering stage의 bias나 fixed filtering의 parameter를 변경함으로써 gain과 resonance를 globally scaling 하거나 frequency response를 left/right로 shift 할 수 있음
    - External control의 'action'은 learned HC matrix의 element를 adjusting 함으로써 변경될 수 있음

3. Experiments

- Settings

• $S=10$의 cascaded filtering stage와 $C_{\max} = 6$의 external parameter를 가지는 BOSS MT-2 distortion pedal을 emulate
  - Distorted audio는 analog cirucit의 SPICE 모델을 사용하여 생성됨
• Comparisons : WaveNet

Conditioning Site

- Results

• 제안된 방식은 WaveNet보다 100배 더 적은 parameter를 가지면서 WaveNet과 비교하여 경쟁력 있는 MSE 성능을 달성

모델 성능 비교

• MUSHRA 기반의 품질 비교에서도 제안된 방식은 WaveNet에 버금가는 청취 품질을 달성

청취 품질 비교

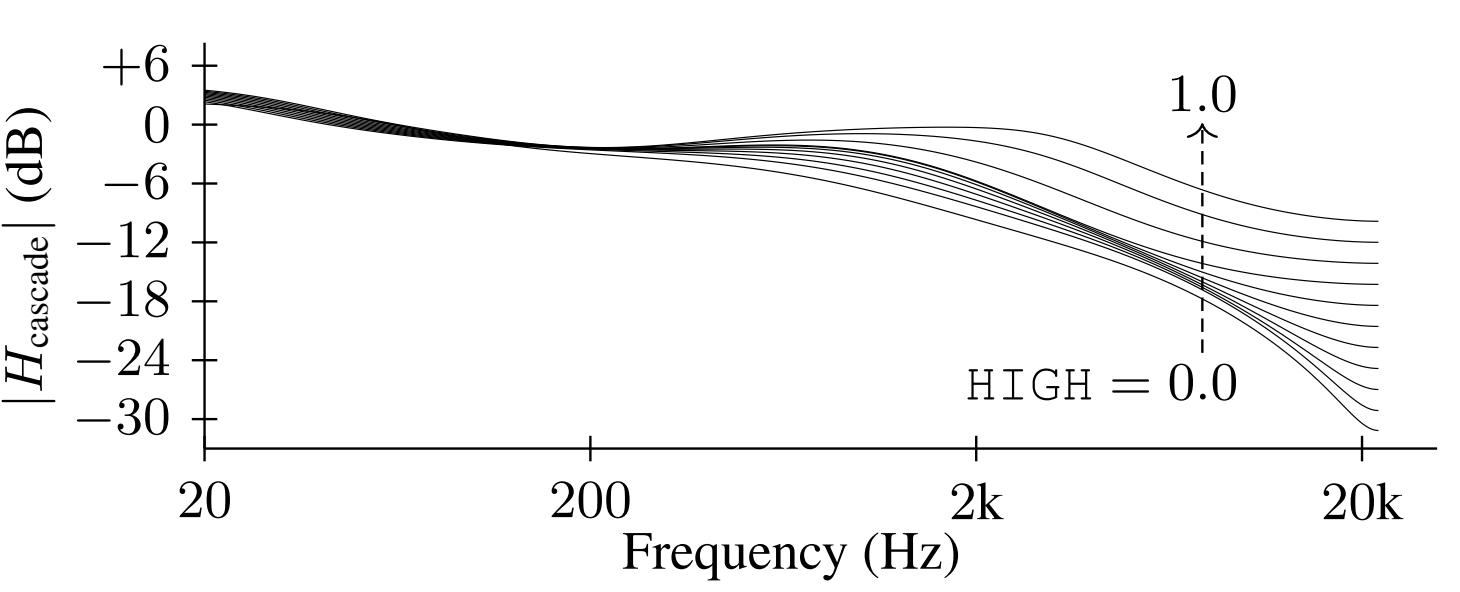
• 특히 제안된 방식은 hyperconditiong을 활용함으로써 직관적인 방식으로 filter frequency response를 변경할 수 있음
  - i.e.) HIGH parameter를 늘리면 high end에서 6 stage의 response가 증가함

HIGH에 따른 MT-2 Magnitude Response