[Paper 리뷰] End-to-End LPCNet: A Neural Vocoder with Fully-Differentiable LPC Estimation

End-to-End LPCNet: A Neural Vocoder with Fully-Differentiable LPC Estimation

---

• Neural vocoder는 여전히 우수한 합성 품질에 비해 높은 computational complexity가 요구됨
• End-to-End LPCNet
  • Linear prediction에 기반한 autoregressive model을 사용하여 neural vocoding의 complexity를 완화
  • 추가적으로 frame rate network의 input feature에서 linear prediction cofficient를 예측하는 방법을 학습하여 기존 end-to-end version을 구성
• 논문 (INTERSPEECH 2022) : Paper Link

---

1. Introduction

• Vocoder는 acoustic parameter를 기반으로 intelligible speech를 합성하는 것을 목표로 함
  • BUT, WaveNet, WaveRNN과 같은 기존 neural vocoder는 real-time 합성을 위해서는 강력한 GPU/CPU가 요구됨
  • 한편 LPCNet은 WaveRNN을 기반으로 linear prediction (LP)와 source-filter model을 도입하여 고품질의 합성 성능을 유지하면서 3 GFLOPS의 computational cost를 줄일 수 있음
    1. BUT, LPCNet은 추론 시 acoustic feature로부터 LP coefficient를 explicit computation 해야 하는 한계점이 있음
    2. 결과적으로 arbitrary latent feature space를 사용하기 어려우므로 end-to-end coding이나 input이 full clean spectrum을 나타내지 않는 경우 사용하기 어려움

-> 그래서 기존 LPCNet의 explicit LPC computation을 회피하고 fully-differentiable 구성을 적용한 End-to-End LPCNet을 제안

 

• End-to-End LPCNet
  • 기존 LPCNet을 개선하여 End-to-End differentiable LPCNet을 구성
  • 이후 loss function으로부터 gradient를 backpropagating 하여 input feature를 통해 LPC estimation을 학습

< Overall of End-to-End LPCNet >

• Explict LPC computation을 회피하는 fully-differentiable LPCNet
• 결과적으로 LPCNet과 동일한 수준의 품질을 유지하면서 추론 속도를 개선

2. LPCNet Overview

• WaveRNN은 conditioning information으로부터 time $t$의 각 sample $s_{t}$에 대한 discrete probability distribution function (PDF) $p(s_{t})$와 $s_{t-1}$까지의 past sample을 예측함
  • 구조적으로는 GRU를 기반으로 linear layer와 softmax activation을 적용해 distribution을 output 함
    - 이때 GRU의 computational requirement를 줄이기 위해 block-sparse wegith matrix를 사용
  • LPCNet은 linear prediction을 사용하여 WaveRNN을 simplify 함
    1. 먼저 LP coefficient $a_{i}$는 Levinson-Durbin Algorithm을 따라 input cepstral feature를 spectrum으로 변환하여 autocorrelation을 얻는 방식으로 explicitly compute 됨
    2. 이후 얻어진 LPC는 previous sample에서 예측 $p_{t}$를 계산하는 데 사용됨:
       (Eq. 1) $p_{t}=\sum_{i=1}^{M}a_{i}s_{t-i}$
       - $M$ : prediction order (16kHz LPCNet의 경우 $M=16$을 사용)
       - $e_{t}=s_{t}-p_{t}$ : excitation/residual
    3. 그러면 main GRU $\text{GRU}_{A}$는 past signal $s_{t-1}$ 뿐만 아니라 past excitation $e_{t-1}$과 current sample $p_{t}$의 예측에도 사용할 수 있음
       - 여기서 output은 excitation distribution $P(e_{t})$를 추정
  • 한편 full 16-bit PDF를 output 할 때 LPCNet은 $\mu$-law scale을 채택하여 WaveRNN의 two-pass coarse-fine strategy를 회피함:
    (Eq. 2) $U(x)=\text{sgn}(x)\cdot \frac{U_{\max}\log (1+\mu |x|)}{\log (1+\mu)}$
    - 여기서 $\mu$-law range $U_{\max}=128$이고 $\mu=255$, $U(0)=0$
    - $\mu$-law value는 일반적으로 $[0,256]$ range의 양수값을 가지지만, 논문에서는 $[-128,128]$을 가지도록 함
    
  • $\mu$-law scale은 quantization noise를 signal amplitude와 independent 하도록 만드는 역할
    1. Input에 적용된 pre-emphasis filter $E(z)=1-\alpha z^{-1}$는 8-bit $\mu$-law quantization에서 발생하는 audible quantization noise를 방지함
    2. De-emphasis filter $D(z)=\frac{1}{1-\alpha z^{-1}}$는 synthesis output에 적용됨
       - $\alpha=0.85$를 사용
  • Frame rate network는 cepstral feature로부터 frame conditioning feature $\mathbf{f}$를 학습함
    - Sample rate network는 frame conditioning feature $\mathbf{f}$와 prediction $p_{t}$, past excitation $e_{t-1}$, past signal $s_{t-1}$을 기반으로 excitation $e_{t}$에 대한 output probability distribution을 예측

3. End-to-End LPCNet

• End-to-End LPCNet은 LPC computation이 cepstral feature의 fixed set으로 hardcode 되지 않고 differentiable computation을 지원하는 것을 목표로 함
  • 구조적으로는 아래 그림과 같이 frame rate network가 LPC를 계산하는데 사용됨
  • 이때 fully-differentiable end-to-end training을 위해서는 다음을 differentiable 하게 구성해야 함:
    1. LPC Computation
    2. Input Embedding
    3. Loss Function Computation

Overall of End-to-End LPCNet

- Learning to Compute LPCs

• LP coefficient는 error에 민감하고 unstable 하므로 directly quantize 하거나 estimate 할 수 없음
  • Robust representation으로 $[-1,1]$ interval 내에서 stability를 보장하는 Reflection Coefficient (RC)나 alternating ordering을 따르는 line spectral frequency를 고려할 수 있음
  • 따라서 논문에서는 representation으로 RC를 채택하여 사용함
    1. $[-1,1]$ interval이 $\tanh$ activation으로 쉽게 enforce 되고, pre-tanh logit이 RC의 log-area ratio representation과 동일하기 때문
    2. 여기서 RC는 Levinson recursion을 통해 direct-form LP coefficient로 변환됨:
       (Eq. 3) $a_{j}^{(i)}=\left\{\begin{matrix}
       k_{i}, & \text{if}\,\, j=i \\
       a_{j}^{(i-1)}+k_{i}a_{i-j}^{(i-1)}, & \text{otherwise} \\
       \end{matrix}\right.$
       - $k_{i}$ : RC, $a_{j}^{(i)}$ : order $i$의 $j$-th prediction coefficient
    3. 결과적으로 (Eq. 1), (Eq. 3)은 differentiable 하므로 network는 RC를 계산하는 방법을 학습할 수 있음
  • 추가적으로 End-to-End LPCNet은 frame rate network condition vector $\mathbf{f}$의 첫 $M$ element를 RC로 directly use 함
    - 이를 통해 다음 sample rate network가 estimated prediction coefficient를 고려하도록 보장할 수 있음
    - (Eq. 3)과 cepstral-to-LPC conversion은 전체 complexity에 비해 무시할 수 있으므로, 기본적으로 End-to-End LPCNet은 기존 LPCNet과 동일한 complexity를 가짐

- Differentiable Embedding Layer

• Input $p_{t}, s_{t-1}, e_{t-1}$은 8-bit $\mu$-law value로 quantize 되어 input sample embedding을 학습하는데 사용됨
  • 이때 embedding은 input에 적용되는 non-linear function을 학습하여 singal value를 GRU에 대한 input으로 직접 사용하는 것에 비해 합성 품질을 크게 향상할 수 있음
    - BUT, $\mu$-law quantization은 gradient가 frame rate network의 RC computation까지 loss를 backpropagate 하는 것을 방지함
  • 따라서 논문은 embedding을 differentiable 하게 구성하기 위해, interpolation scheme을 도입함
    
    1. 먼저 $\mathbf{v}_{j}$를 embedding matrix의 $j$-th embedding vector라 하고, $x$를 real-valued (unquantized) $\mu$-law sample value라고 하자
    2. 그러면 interpolated embedding $\mathbf{v}^{(i)}(x)$는:
       (Eq. 4) $f=x-\lfloor x\rfloor$
       (Eq. 5) $\mathbf{v}^{(i)}(x)=(1-f)\cdot \mathbf{v}_{\lfloor x\rfloor}+f\cdot \mathbf{v}_{\lfloor x\rfloor +1}$
       - 이를 통해 gradient는 fractional interpolation coefficient $f$를 통해 propagate 될 수 있음
  • 추론 시에는 interpolation의 extra complexity를 회피하고, $\mathbf {v}(x)=\mathbf {v}_{\lfloor x\rceil}$를 계산함
    - $\lfloor \cdot \rceil$ : rounding operation

- Loss Function

• 기존 LPCNet은 DNN training 이전에 excitation을 pre-compute 할 수 있지만, 논문의 End-to-End LPCNet에서 excitation은 DNN architecture의 일부로 계산됨
  • 따라서 cross-entropy loss에 대한 ground-truth target은 constant 하지 않으므로 loss function에서 다음의 문제가 발생함
    1. Target $\mu$-law excitation을 quantize 하면 gradient가 RC computation으로 backpropagate 되지 않음
    2. $\mu$-law scale의 non-linear nature로 인해 large excitation value는 $\mu$-law spacing이 크고 narrow excitation value의 경우 0에 가까운 값을 가짐
       - 결과적으로 동일한 linear uncertainty라도 excitation이 크면 cross-entropy 값이 커질 수 있음
  • 먼저 첫 번째 문제를 해결하기 위해 논문은 interpolated cross-entropy loss를 도입함
    1. $e_{t}^{(\mu)}$를 time $t$에서의 real-valued $\mu$-law excitation이라고 하고, $\hat{P}(e_{t}^{(\mu)})$를 time $t$에서 추정된 discrete probability라고 하자
    2. 여기서 앞선 interpolated embedding과 같이 standard cross-entropy 대신 nearest integer로 round 하면:
       (Eq. 6) $\mathcal{L}_{CE}=\mathbb{E}\left[-\log \hat{P}\left(\lfloor e_{t}^{(\mu)}\rceil \right)\right]$
    3. 해당 loss는 다음과 같이 time에 따라 distribution의 기댓값을 취하여 probability를 interpolate 함:
       (Eq. 7) $f=e_{t}^{(\mu)}-\lfloor e_{t}^{(\mu)}\rfloor$
       (Eq. 8) $\hat{P}^{(i)}\left(e_{t}^{(\mu)}\right)=(1-f)\hat{P}\left(\lfloor e_{t}^{(\mu)}\rfloor\right)+f \hat{P}\left(\lfloor e_{t}^{(\mu)}\rfloor +1\right)$
       (Eq. 9) $\mathcal{L}_{ICE}=\mathbb{E}\left[-\log \left(\hat{P}^{(i)}\left(e_{t}^{(\mu)}\right)\right)\right]$
       - $f$ : interpolation coefficient
  • 다음으로 두 번째 문제를 해결하기 위해서는 linear-domain excitation sample의 distribution에 해당하는 cross-entropy loss를 최소화해야 함
    1. 이는 $\hat{P}^{(i)}(\cdot)$을 $\mu$-law value와 1 차이에 해당하는 linear step size로 dividing 하는 것으로 수행될 수 있음
    2. 이때 $\mu$-law expansion function $U^{-1}(\cdot)$의 derivative로 나누어 compensated loss를 얻음:
       (Eq. 10) $\mathcal{L}_{C}=\mathbb{E}\left[-\log \frac{\hat{P}^{(i)}\left( e_{t}^{(\mu)}\right)}{\frac{d}{dx} U^{-1}(x)|_{e_{t}^{(\mu)}}}\right]$
    3. $U^{-1}(\cdot)$은 piecewise exponential 하므로, contant term을 discard 하여 (Eq. 10)을 단순화하면:
       (Eq. 11) $\mathcal{L}_{C}=\mathcal{L}_{ICE}+\mathbb{E}\left[\frac{|e_{t}^{(\mu)} | \log (1+\mu)}{U_{\max}}\right]$
       - $\mathcal{L}_{ICE}$ : (Eq. 9)의 interpolated cross-entropy loss
       - 오른쪽 term : $\mu$-law companded excitation에서 $L_{1}$ loss로 $\mu$-law scale을 compensate

- Regularization

• Compensated loss $\mathcal{L}_{C}$만 사용하면 optimization이 발산하므로, training stability를 위해 논문은 다음의 3가지 regularization variant를 고려함
  1. $L_{1}$ Regularization
     
     • (Eq. 11)의 $\mu$-law compensation에는 $L_{1}$ loss가 이미 포함되어 있으므로 다음과 같이 compensation term을 artificially increase 하는 regularizer를 도입:
       (Eq. 12) $\mathcal{L}_{L_{1}}=\gamma \mathbb{E}\left[ \frac{\left| e_{t}^{(\mu)} \right|\log (1+\mu)}{U_{\max}}\right]$
       - 여기서 $\gamma=1$을 사용해 (Eq. 11)의 compensation term을 두배로 늘림으로써 training을 stabilize 함
     • 실제로 regularization은 standard LPC analysis와 유사한 방식으로 prediction error를 최소화함
       - 특히 $\mu$-law residual에 대한 연산은 regularization이 high-/low-amplitude signal에 거의 동일하게 적용되는 특성을 가짐
  2. Log-Area Ratio Regularization
     
     • 기존 LPCNet과 같이 ground-truth LPC에 대해 directly match 하는 방식을 고려할 수 있음
       - 해당 regularization에서 LPC는 target speech signal에 대해서만 계산되고, training time에만 사용되므로 End-to-End LPCNet의 complexity를 증가시키지 않음
     • 이때 추정된 RC $k_{i}$와 ground-truth RC $k^{(g)}$ 간의 distance로써, 두 filter 간의 difference를 나타내는 log-area ratio (LAR)을 사용:
       (Eq. 13) $\mathcal{L}_{LAR}=\mathbb{E}\left[ \sum_{i}\left(\log \frac{1-k_{i}}{1+k_{i}}-\log \frac{1-k_{i}^{(g)}}{1+k_{i}^{(g)}}\right)^{2}\right]$
  3. Log-Area Ratio Matching
     • (Eq. 6)의 non-compensated standard discrete cross-entropy를 사용하면서 LPC estimation을 adapt 하기 위해 (Eq. 13)을 적용하는 방식
     • 이때 LPC는 output probability estimation을 고려하지 않고 ground-truth LPC와 match 되도록 함
       - Excitation은 예측된 LP coefficient를 기반으로 계산됨

4. Experiments

- Settings

• Dataset : 9 TTS datasets
• Comparisons : LPCNet

- Results

• 여러 end-to-end variant에 대한 성능을 비교해 보면, LAR-regularized model이 ground-truth와 가장 비슷한 것으로 나타남

추정된 LPC와 Ground-Truth LPC 간의 Log-Spectral Distance (LSD)

각 Variant별 LPC Response 비교

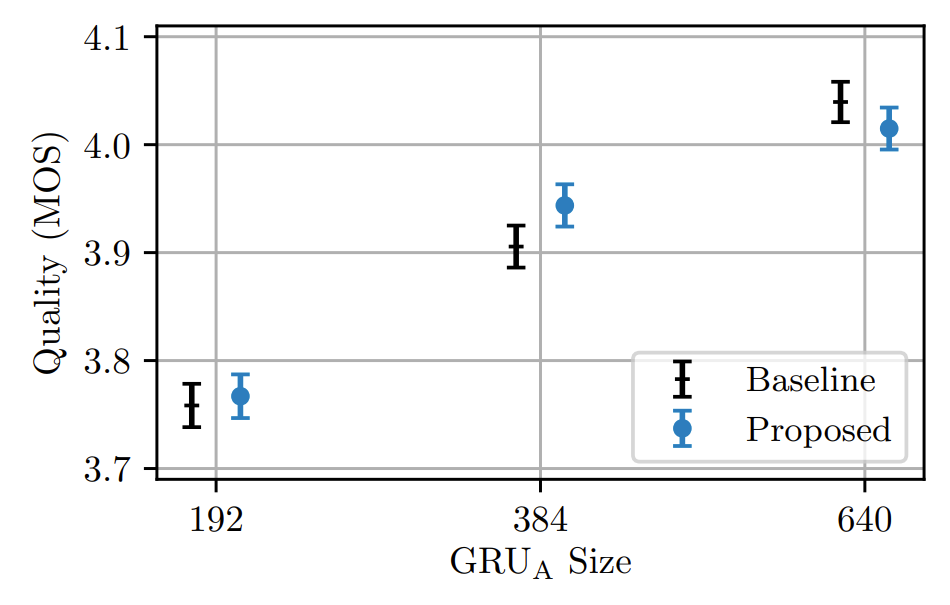
• MOS 측면에서도 LAR-regularized model이 가장 우수한 성능을 달성함

MOS 비교

Baseline LPCNet과의 비교