[Paper 리뷰] Efficient Neural Music Generation

Efficient Neural Music Generation

---

• MusicLM은 semantic, coarse acoustic, fine acoustic modeling을 통해 뛰어난 음악 생성 능력을 보여주고 있음
• BUT, MuiscLM은 fine-grained acoustic token을 얻기 위해 많은 계산 비용이 필요함
• MeLoDy
  • 고품질의 음악 생성이 가능하면서 forward pass의 효율성을 개선한 LM-guided diffusion model
  • Semantic modeling을 위해 MusicLM을 inherit 하고 dual-path diffusion과 audio VAE-GAN을 사용하여 conditioning semantic token을 waveform으로 decoding
  • 특히 dual-path diffusion은 각 denoising step에서 cross-attention을 통해 효과적으로 semantic information을 latent segment에 반영하고, coarse-/fine-acoustics를 simultaneously modeling 함
• 논문 (NeurIPS 2024) : Paper Link

---

1. Introduction

• Language Model (LM)은 long-term context 측면에서 complex relationship을 반영하는데 뛰어나고, 특히 AudioLM은 LM을 audio 합성 문제에 도입하여 우수한 성능을 달성했음
  • 한편으로 diffusion probabilistic model (DPM)도 음성/음악 생성에서 좋은 성능을 보이고 있음
    
  • BUT, LM을 통해 free-form text로부터 적절한 음악을 생성하는 것에는 여전히 한계가 있음
    - Permissible music description이 매우 다양하고, genre, insturments, tempo 등이 서로 밀접하게 연관되어 있기 때문
  • 이를 위해 MusicLM, Noise2Music 등은 large-scale dataset을 기반으로 training 되어 높은 수준의 음악 생성 성능을 달성함
    - BUT, 두 방법 모두 합성 성능에 비해 computational cost 측면에서 상당한 제약이 있음

-> 그래서 음악 생성 LM의 효율성을 개선한 MeLoDy를 제안

 

• MeLoDy
  • LM과 DPM을 모두 활용하는 LM-guided diffusion model
  • MusicLM의 highest-level LM (Semantic LM)을 활용하여 음악의 semantic structure를 모델링하고, melody/rhythm/dynamics/timbre/tempo 등에 대한 전반적인 arrangement를 결정
  • 해당 Semantic LM을 condition으로 하여 sampling acceleration을 통한 효율성 개선을 가능하게 하기 위해, DPM의 non-autoregressive nature를 활용

< Overall of MeLoDy >

• 고품질 음악 합성과 빠른 sampling이 가능한 LM-guided diffusion model
• Semantic conditioning strategy와 함께 coarse-/fine-acoustic information을 효율적으로 모델링하는 Dual-Path Diffusion model을 도입
• 추가적으로 DPD에 대해 생성 품질을 향상할 수 있는 sampling method을 설계하고 continuous latent representation을 효과적으로 학습할 수 있는 audio VAE-GAN을 구성
• 결과적으로 합리적인 합성 품질을 유지하면서 기존보다 빠른 음악 합성이 가능

2. Background on Audio Language Modeling

- Audio Language Modeling with MusicLM

• MusicLM은 AuidoLM의 audio language modeling framework를 따르고, 이때 audio 합성은 coarse-to-fine audio token에 대한 language modeling task로 볼 수 있음
  • 이때 AudioLM은 다음의 2가지 tokenization을 사용함:
    1. Semantic Tokenization : w2v-BERT와 같은 SSL의 representation에 대한 $K$-means
    2. Acoustic Tokenization : SoundStream과 같은 neural audio codec
  • 이때 acoustic token의 hierarchical structure를 더 잘 처리하기 위해 AudioLM은 acoustic token을 coarse/fine stage로 분리하여 사용
  • 즉, AudioLM은 semantic modeling, coarse acoustic modeling, fine acoustic modeling의 3가지 LM task를 처리함
    1. 먼저 conditioning token sequence를 $\mathbf{c}_{1:T_{\text{end}}}:=[\mathbf{c}_{1},...,\mathbf{c}_{T_{\text{end}}}]$라 하고, target token sequence를 $\mathbf{u}_{1:T_{\text{tgt}}}:=[\mathbf{u}_{1},...,\mathbf{u}_{T_{\text{tgt}}}]$라 하자
    2. 그러면 각 modeling task에서 $\theta$로 parameterize 된 Transformer encoder-decoder language model은 다음의 autoregressive modeling 문제를 해결함:
       (Eq. 1) $p_{\theta}(\mathbf{u}_{1:T_{\text{tgt}}}|\mathbf{c}_{1:T_{\text{end}}})=\prod_{j=1}^{T_{\text{tgt}}}p_{\theta}(\mathbf{u}_{j}|[\mathbf{c}_{1},...,\mathbf{c}_{T_{\text{end}}},\mathbf{u}_{1},...,\mathbf{u}_{j-1}])$
       - 여기서 conditioning token은 prefix로 target token에 concatenate 됨
       
  • AudioLM에서 semantic modeling은 condition을 취하지 않음
    - 한편으로 coarse acoustic modeling은 semantic token을 condition으로 사용하고, fine acoustic modeling은 coarse acoustic token을 condition으로 사용함
    - 이때 각 3가지 LM은 ground-truth token에 대해 parallel 하게 training 될 수 있지만, 추론 시에는 sequentially sampling 되어야 함

- Joint Tokenization of Music and Text with MuLan and RVQ

• Audio-only training을 위해 MusicLM은 large-scale music dataset과 weakly-associated, free-form text annotation을 사용하여 개별적으로 pre-train 된 joint audio-text embedding model인 MuLan을 사용함
  • MuLan은 paired audio-text embedding이 최대한 가까워지도록 music audio와 해당 text description을 동일한 embedding space에 project 하는 방법을 학습함
  • 그리고 separately learned Residual Vector Quantization (RVQ) module을 사용하여 text와 musice의 embedding을 tokenize 함
  • 이후 text prompt에서 음악을 생성하기 위해 (Eq. 1)을 따라 semantic modeling과 coarse acoustic modeling에서 RVQ의 MuLan token을 conditioning token으로 사용함
  • 결과적으로 prefixing MuLan token이 주어지면, semantic token, coarse acoustic token, fine acoustic token이 LM을 통해 계산되어 text prompt에 해당하는 음악 audio가 생성됨 

3. Model Description

• MeLoDy의 전체 training/sampling pipeline은 아래 그림과 같음
  • 이때 MeLoDy의 representation learning을 위해 3가지 module을 사용함:
    
    1. MuLan
    2. wav2vec2-Conformer
    3. Audio VAE와 2개의 generative model
       - Semantic, acoustic modeling을 위한 language model (LM)
       - Dual-Path Diffusion (DPD) model
  • MeLoDy 역시 MusicLM과 비슷하게 LM을 활용하여 long-term context 측면에서 음악의 complex relationship을 모델링하고, conditioning token을 얻기 위해 MuLan을 pre-training 함
  • 추가적으로 semantic tokenization을 위해 wav2vec2와 동일한 architecture를 사용하지만, transformer 대신 conformer를 채택한 wav2vec2-conformer를 사용

MeLoDy의 Training/Sampling Pipeline

- Audio VAE-GANs for Latent Representation Learning

• Arbitraily high-variance latent representation을 학습하는 것을 방지하기 위해 도입된 Latent Diffusion Model (LDM)에 대한 KL-regularized autoencoder는 우수한 stability를 보여주었음
  • 해당 autoencoder는 VAE와 유사한 방식으로 encoder output에 KL-penalty를 impose 하지만, Generative Adversarial Network (GAN)과 같이 adversarially training 됨
    - 논문에서는 이러한 방식을 VAE-GAN이라고 하고, 해당 구조를 audio generation을 위해 도입함
  • 따라서 audio VAE-GAN은 96 striding factor로 24kHz audio를 reconstruct 하도록 training 되어 250kHz latent sequence를 생성함
    1. Encoder의 경우 decoder의 upsampling module을 convolution-based down-sampling module로 replacing 하여 구성됨
    2. Adversarial training을 위해 HiFi-GAN의 Multi-Period Discriminator와 UnivNet의 Multi-Resolution Spectrogram Discriminator를 사용함

- Dual-Path Diffusion: Angle-Parameterized Continuous-Time Latent Diffusion Models

• Dual-Path Diffusion (DPD) model은 continuous-time의 diffusion probabilistic model (DPM)에 대한 variant와 같음 
  • LDM과 비슷하게 raw data space $\mathbf{x}\sim p_{\text{data}}(\mathbf{x})$에서 직접 동작하는 대신, DPD는 audio가 latent vector $\mathbf{x}\approx \mathcal{D}(\mathbf{z}_{0})$에서 approximately reconstruct 될 수 있도록 low-dimensional latent space $\mathbf{z}_{0}=\mathcal{E}_{\phi}(\mathbf{x})$에서 동작함
    - $\mathcal{E}, \mathcal{D}$ : 각각 VAE-GAN의 encoder, decoder
  • 이와 같이 latent space를 diffusion 함으로써 DPM의 computational burden을 크게 줄일 수 있음
    - Diffusion model의 output을 활용하면 audio VAE-GAN은 다른 VQ-based autoencoder 안정적으로 동작 가능함
  • DPD는 2개의 strictly positive scalar-valued, continuously differentiable function $\alpha_{t}, \sigma_{t}$로 fully specifiy 되는 Gaussian diffusion process $\mathbf{z}_{t}$로써: $q(\mathbf{z}_{t}|\mathbf{z}_{0})=\mathcal{N}(\mathbf{z}_{t};\alpha_{t}\mathbf{z}_{0},\sigma^{2}_{t}I),\,\,\, \forall t\in[0,1]$
    1. 여기서 trigonometric property를 통해 $\alpha_{t}:=\cos(\pi t/2),\,\sigma_{t}:=\sin(\pi t/2)$를 정의할 수 있고, 이때 variance-preserving과 같이 $\sigma_{t}=\sqrt{1-\alpha_{t}^{2}}$이 됨
    2. 해당 definition을 기반으로 $\mathbf{z}_{t}$의 diffusion process는 angle $\delta \in[0,\pi /2]$측면에서 reparameterize 될 수 있음:
       (Eq. 2) $\mathbf{z}_{\delta}=\cos(\delta)\mathbf{z}_{0}+\sin(\delta)\epsilon,\,\,\, \epsilon\sim\mathcal{N}(0,I)$
       - 이는 angle $\delta$가 0에서 $\pi/2$로 증가함에 따라 $\mathbf{z}_{\delta}$가 noisy 해진다는 것을 의미함
  • Generative process를 구축하기 위해 $\theta$-parameterized variational model $p_{\theta}(\mathbf{z}_{\delta-\omega}|\mathbf{z}_{\delta})$는 angle에서 any step $\omega\in(0,\delta]$ backward를 취함으로써 diffusion process를 reverse 하도록 training 됨 
    1. 즉, $\pi /2$를 $T$ finite segment로 discretizing 함으로써 $T$ sampling step에서 $\mathbf{z}_{\pi /2}\sim\mathcal{N}(0,I)$로부터 $\mathbf{z}_{0}$을 생성 가능:
       (Eq. 3) $p_{\theta}(\mathbf{z}_{0}|\mathbf{z}_{\pi /2})=\int_{\mathbf{z}_{\delta_{1:T-1}}}\prod_{t=1}^{T}p_{\theta}(\mathbf{z}_{\delta_{t}-\omega_{t}}|\mathbf{z}_{\delta_{t}})d\mathbf{z}_{\delta_{1:T-1}}, \,\,\, \delta_{t}=\left\{\begin{matrix}
       \frac{\pi}{2}-\sum_{i=t+1}^{T}\omega_{i}, & 1\leq t<T\\
       \frac{\pi}{2}, & t=T \\
       \end{matrix}\right.$
       - $\omega_{1},...,\omega_{T}$ : angle schedule로써 $\sum_{t=1}^{T}\omega_{t}=\pi /2$를 만족
    2. Angle schedule 선정과 관련하여 모든 $t$에 대해 $\omega_{t}=\frac{\pi}{2T}$와 같은 uniform 방식을 고려할 수 있음
       - BUT, noise scheduling은 sampling 시작에서는 larger step을 취하고 refinement를 거치며 점점 step이 작아지는 경향이 있음
    3. 따라서 MeLoDy에서는 다음의 linear angle schedule을 사용함:
       (Eq. 4) $\omega_{t}=\frac{\pi}{6T}+\frac{2\pi t}{3T(T+1)}$
       - 이를 통해 보다 stable 하고 고품질의 결과를 얻을 수 있음

Dual-Path Diffusion (DPD) model

• Diffusion Velocity Prediction
  • DPD에서는 $\mathbf{v}_{\delta}:=\frac{d\mathbf{z}_{\delta}}{d\delta}$로 정의된 $\delta$에서의 diffusion velocity를 모델링함 
  • 이를 simplify 하면:
    (Eq. 5) $\mathbf{v}_{\delta}=\frac{d\cos(\delta)}{d\delta}\mathbf{z}_{0}+\frac{d\sin(\delta)}{d\delta}\epsilon=\cos(\delta)\epsilon-\sin(\delta)\mathbf{z}_{0}$
    - 여기서 $\mathbf{z}_{0}=\cos(\delta)\mathbf{z}_{\delta}-\sin(\delta)\mathbf{v}_{\delta}$이므로, $\mathbf{v}_{\delta}$가 주어지면 임의의 $\delta$에서 noisy latent $\mathbf{z}_{\delta}$로 부터 original sample $\mathbf{z}_{0}$를 쉽게 얻을 수 있음
    - 이는 $\mathbf{v}_{\delta}$가 neural network prediction $\hat{\mathbf{v}}_{\theta}(\mathbf{z}_{\delta};\mathbf{c})$에 대한 feasible target 임을 의미함
    - $\mathbf{c}$ : music generation을 control 하는 conditions set
  • MeLoDy는 training 중에는 SSL model로부터 얻어지고, 추론 시에는 LM에 의해 생성되는 semantic token $\mathbf{u}_{1},...,\mathbf{u}_{T_{\text{ST}}}$ 을 사용하여 DPD를 condition 함
    - 이때 token-based discrete condition을 사용하여 음악의 semantics를 control 하고, diffusion model이 각 token 자체에 대한 embedding vector를 학습하도록 하면 generation stability가 향상됨
  • 결과적으로 해당 velocity prediction network $\theta$는 Mean Squared Error (MSE) loss를 통해 training 됨:
    (Eq. 6) $\mathcal{L}:=\mathbb{E}_{\mathbf{z}_{0}\sim p_{\text{data}}(\mathbf{z}_{0}), \epsilon\sim\mathcal{N}(0,I),\delta\sim\mathrm{Uniform}[0,1]}\left[ || \cos(\delta)\epsilon-\sin(\delta)\mathbf{z}_{0}-\hat{\mathbf{v}_{\theta}}(\cos(\delta)\mathbf{z}_{0}+\sin(\delta)\epsilon;\mathbf{c})||_{2}^{2}\right]$
    - 이는 DPD training loss의 basis로 사용됨

• Multi-Chunk Velocity Prediction
  • Long-context generation의 경우, 새로운 random noise chunk를 점진적으로 추가하는 것으로 audio generation을 infinitely continue 할 수 있음
  • 이를 위해서는 각 chunk가 서로 다른 scale의 noisiness를 나타내는 chunked input을 처리할 수 있도록 velocity prediction network를 training 해야 함
    1. 먼저 $M$개의 velocity chunk로 구성된 multi-chunk velocity target $\mathbf{v}_{\text{tgt}}$가 있다고 하자
    2. $\mathbf{z}_{0}, \mathbf{z}_{\delta},\epsilon\in\mathbb{R}^{L\times D}$가 주어졌을 때 $L$ length를 나타내고 $D$가 latent dimension을 나타낸다고 하면, $\mathbf{v}_{\text{tgt}}:=\mathbf{v}_{1}\oplus ...\oplus \mathbf{v}_{M}$을 얻을 수 있고, 여기서:
       (Eq. 7) $\mathbf{v}_{m}:=\cos(\delta_{m})\epsilon[L_{m-1}:L_{m},:]-\sin(\delta_{m})\mathbf{z}_{0}[L_{m-1}:L_{m},:], \,\,\, L_{m}:=\left\lfloor \frac{mL}{M}\right\rfloor$
       - $\oplus$ : concatentation
       - 여기서 NumPy slicing을 활용하여 $m$-th chunk를 얻을 수 있고, 각 training에서 각 chunk에 대해 $\delta_{m}\sim\textrm{Uniform}[0,\pi /2]$를 draw 하여 noise scale을 결정함
  • 그러면 (Eq. 6)의 MSE loss는 다음과 같이 확장됨:
    (Eq. 8) $\mathcal{L}_{\text{multi}}:=\mathbb{E}_{\mathbf{z}_{0},\epsilon,\delta_{1},...,\delta_{M}}\left[ ||\mathbf{v}_{\text{tgt}}-\hat{\mathbf{v}}_{\theta}(\bar{\mathbf{z}}_{\delta_{1}}\oplus ... \oplus \bar{\mathbf{z}}_{\delta_{M}};\mathbf{c}) ||_{2}^{2}\right]$
    (Eq. 9) $\bar{\mathbf{z}}_{\delta_{M}}:=\cos(\delta_{m})\mathbf{z}_{0}[L_{m-1}:L_{m},:]+\sin(\delta_{m})\epsilon[L_{m-1}:L_{m},:]$
  • Network input에 global noise scale을 사용하는 기존 방식과 달리, multi-chunk prediction은 모든 $M$ chunk에 대한 noise scale이 무엇인지를 network에 specifically inform 해야 함
  • 따라서 condition set $\mathbf{c}:=\{\mathbf{u}_{1},...,\mathbf{u}_{T_{\text{ST}}},\delta\}$에 angle vector $\delta$를 추가하여 $L$-length input에 대해 align 된 모든 $M$ chunk의 angle을 draw 함:
    (Eq. 10) $\delta :=[\delta_{1}]_{r=1}^{L_{1}}\oplus...\oplus[\delta_{M}]_{r=1}^{L_{M}}\in\mathbb{R}^{L}$
    - $[a]_{r=1}^{B}$ : $B$-length vector를 만들기 위해 scalar $a$를 $B$번 repeating 하는 operation

• Dual-Path Modeling for Efficient and Effective Velocity Prediction
  • $\hat{\mathbf{v}}_{\theta}$를 사용하여 multi-chunk velocity를 예측하기 위해 Dual-Path Modeling mechanism을 도입함
    - Coarse, fine path를 따라 효율적인 parallel processing을 가능하게 하고 DPD의 semantic conditioning에 도움을 줌
  • 이때 DPD에서 $\{\mathbf{u}_{1}, ..., \mathbf{u}_{T_{\text{ST}}}, \delta \}$ condition이 처리되는 과정은 다음과 같음
  • Encoding Angle Vector
    1. 먼저 latent의 frame-level noise scale을 record하는 $\delta\in\mathbb{R}^{L}$을 encode하고, 
    2. Classical positional encoding 대신 2개의 learnable vector $\mathbf{e}_{\text{start}}, \mathbf{e}_{\text{end}}$에 대한 spherical interpolation $\otimes$을 사용:
       (Eq. 11) $\mathbf{E}_{\delta}:=\text{MLP}^{(1)}(\sin(\delta)\otimes\mathbf{e}_{\text{start}}+\sin(\delta)\otimes\mathbf{e}_{\text{end}})\in\mathbb{R}^{L\times D_{\text{hid}}}$
    3. 즉, 모든 $i$에 대해, $\text{MLP}^{(i)}(\mathbf{x}):=\text{RMSNorm}(\mathbf{W}_{2}^{(i)}\text{GELU}(\mathbf{xW}_{1}^{(i)}+\mathbf{b}_{1}^{(i)})+\mathbf{b}_{2}^{(i)})$는 arbitary input $\mathbf{x}\in\mathbb{R}^{D_{\text{in}}}$을 $\mathbb{R}^{D_{\text{hid}}}$로 project함
       - 이때 learnable $\mathbf{W}^{(i)}_{1}\in\mathbb{R}^{D_{\text{in}}\times D_{\text{hid}}}, \mathbf{W}_{2}^{(i)}\in\mathbb{R}^{D_{\text{hid}}\times D_{\text{hid}}}, \mathbf{b}_{1}^{(i)}, \mathbf{b}_{2}^{(i)}\in\mathbb{R}^{D_{\text{hid}}}$을 가지는 RMSNorm과 GELU activation을 사용
       - $D_{\text{hid}}$ : hidden dimension
  • Encoding Semantic Tokens
    1. Remaining condition은 semantic information $\mathbf{u}_{1},...,\mathbf{u}_{T_{\text{ST}}}$을 나타내는 discrete token
    2. 먼저 natural language embedding approach를 따라 vector의 lookup table을 사용하여 모든 token $\mathbf{u}_{t}\in\{1,...V_{\text{ST}}\}$을 real-valued vector $E(\mathbf{u}_{t})\in\mathbb{R}^{D_{\text{hid}}}$로 mapping함
       - $V_{\text{ST}}$ : semantic token의 vocabulary size (즉, wav2vec2-Conformer에 대한 $k$-means cluster 수)
       
    3. 이후 time axis를 따라 vector를 stacking 하고 MLP block을 적용하여 $\mathbf{E}_{\text{ST}}:=\text{MLP}^{(2)}([E(\mathbf{u}_{1}),...,E(\mathbf{u}_{T_{\text{st}}})])\in\mathbb{R}^{T_{\text{ST}}\times D_{\text{hid}}}$를 얻음
  • 다음으로, 계산된 embedding $\mathbf{E}_{\delta}, \mathbf{E}_{\text{ST}}$을 condition으로 하여 velocity prediction을 위해 다음을 network input으로 DPD에 제공됨
    - 모든 chunk에 대해 동일한 noise scale $\delta_{t}$을 가지는 경우 $\mathbf{z}_{\delta_{t}}$를 사용하고, 서로 다른 noise scale의 경우 $\bar{\mathbf{z}}_{\delta_{1}}\oplus ... \oplus \bar{\mathbf{z}}_{\delta_{M}}$을 사용
  • Notation을 단순화하기 위해 $\mathbf{z}_{\delta_{t}}$를 network input이라고 하자
    - 그러면 $\mathbf{z}_{\delta_{t}}$는 먼저 linearly transform 된 다음, learnable $\mathbf{W}_{\text{in}}\in\mathbb{R}^{D\times D_{\text{hid}}}$를 가지는 동일한 shape의 angle embedding에 $\mathbf{H}:=\text{RMSNorm}(\mathbf{z}_{\delta_{t}}\mathbf{W}_{\text{in}}+\mathbf{E}_{\delta})$과 같이 추가됨
    - 이후 dual-path modeling을 위해 segmentation operation이 적용됨
  • Segmentation
    1. 아래 그림처럼 segmentation module은 2D input을 length가 $K$인 $S$개의 half-overlapping segment로 나눔
       - 이는 3D tensor $\mathbb{H}:=[0,\mathbf{H}_{1},...,\mathbf{H}_{S},0]\in\mathbb{R}^{S\times K\times D_{\text{hid}}}$로 represent 됨
       - 여기서 $\mathbf{H}_{s}:=\mathbf{H}\left[\frac{(s-1)K}{2}:\frac{(s-1)K}{2}+K,:\right]$, $\mathbb{H}$는 $S=\left\lceil \frac{2L}{K}\right\rceil+1$이 되도록 zero-padding 됨
    2. Segment size를 $K\approx \sqrt{L}$로 선택하면 seqeuence processing cost가 $\mathcal{O}(L)$이 아닌 sub-linear $\mathcal{O}(\sqrt{L})$이 됨
       - 따라서 50Hz codec을 사용하는 MusicLM에 비해 MeLoDy는 매우 긴 sequence도 효율적으로 학습하면서 더 나은 품질을 위한 high-frequency latent도 활용할 수 있음
  • Dual-Path Blocks
    1. Segmentation 이후에는 3D tensor input을 얻고 tensor는 $N$개의 dual-path block으로 전달됨
       - 각 block은 coarse-path (inter-segement), fine-path (intra-segment)에 대한 2개의 processing stage를 포함함
    2. 이때 fine-path processing에는 bi-directional RNN을 사용하고 coarse-path processing에는 attention-based network를 사용하는 것이 좋음
       - 특히 fine acoustic modeling의 목표는 roughly determined audio structure로부터 fine detail을 효과적으로 reconstruction 하는 것임
       - Finer scope에서는 nearby element가 refinement에 필요한 대부분의 information을 포함하고 있기 때문
    3. 따라서 MeLoDy는 Roformer network를 coarse-path 처리에 사용하고, fine-path에 대해서는 2-layer Simple Reccurent Unit (SRU) stack을 사용함
       - 이때 Roformer에서는 rotary positional embedding을 통해 $\mathbf{E}_{\text{ST}}$를 condition으로 사용하기 위해, self-attention과 cross-attention layer를 사용
       - 한편으로 Feature-wise Linear Modulation (FiLM) layer는 SRU의 output에도 적용되어 angle embedding $\mathbf{E}_{\delta}$와 pooled $\mathbf{E}_{\text{ST}}$에 대한 denoising을 지원

Dual-Path Modeling

- Music Generation and Continuation

• Well-trained multi-chunk velocity model $\hat{\mathbf{v}}_{\theta}$가 있고, training에 사용할 latent length $L$에 대해 $L$-length latent generation을 수행한다고 하자
  • 그러면 DDIM sampling은 trigonometric identity를 적용하여 re-formulate 됨:
    (Eq. 12) $\mathbf{z}_{\delta_{t}-\omega_{t}}=\cos(\omega_{t})\mathbf{z}_{\delta_{t}}-\sin(\omega_{t})\hat{\mathbf{v}}_{\theta}(\mathbf{z}_{\delta_{t}};\mathbf{c})$
    - 여기서 (Eq. 4)에서 정의된 $\omega_{t}$를 사용하여 $t=T$에서 $t=1$까지 수행하면, length $L$의 $\mathbf{z}_{0}$ sample을 생성할 수 있음
  • 이후 생성을 continue 하기 위해, 생성된 $\mathbf{z}_{0}$에 random noise로 구성된 새로운 chunk를 추가하고 $\mathbf{z}_{0}$의 첫 번째 chunk를 drop 함
    - 여기서 $\hat{\mathbf{v}}_{\theta}$에 대한 input은 서로 다른 noise scale의 $M$-concatenated noisy latent
  • 따라서 DPD에서 정의된 condition (semantic token/angle vector)는 추론 시 autoregressive nature를 가지기 때문에 generation continuation이 feasible 함
    1. 특히 semantic token은 autoregressive 방식으로 semantic LM에 의해 생성되므로, 새 chunk에 대한 semantic token generation을 continue 할 수 있음
    2. 한편으로 multi-chunk model $\hat{\mathbf{v}}_{\theta}$는 angle vector와 관련하여 다양한 noise scale의 chunk를 처리하도록 training 되므로, 다음과 같이 생성된 audio를 ignore 할 수 있음:
       $\delta_{\text{new}}:=[0]_{r=1}^{L-\lceil L/M\rceil}\oplus[\delta_{t}]_{r=1}^{\lceil L/M\rceil}$
    3. 그러면 새로 추가된 noise chunk는 DDIM sampling의 $\lceil T/M \rceil$ step을 거쳐 meaningful music audio로 변환됨

4. Experiments

- Settings

• Dataset : music dataset (257k hours) & music captions (by ChatGPT)
• Comparisons : Mousai, MusicLM, Noise2Music

Experiment Settings

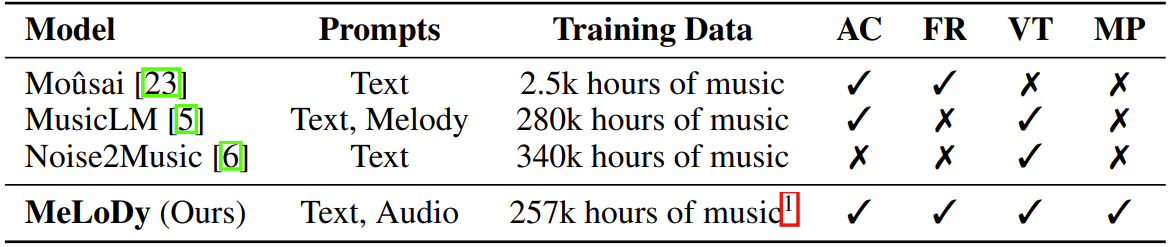
- Results

• Audio quality 측면에서 MeLoDy는 가장 뛰어난 성능을 보이고, musicality와 text correlation 측면에서도 comparable 한 성능을 보임

모델 성능 비교

• 특히 Sampling efficiency 측면에서 MeLoDy는 5 sampling step 만으로도 reference set 보다 높은 MCC score를 달성할 수 있음
  - 생성된 sample을 결정하는 MuLan이 reference audio보다 MusicCaps caption과 더 많이 correlate 되어 있고,
  - DPD는 MusicLM의 nested LM보다 더 낮은 비용으로 MuLan cycle을 consistently completing 할 수 있기 때문

합성 속도 비교

• Ablation study 측면에서 uniform angle schedule과 linear schedule을 비교해 보면,
  • 제안된 linear scehdule을 사용할 때, 적은 수의 sampling step에 대해 acoustic issue를 덜 유발하는 것으로 나타남
  • 한편으로 dual-path architecture도 SNR 측면에서 다른 비교 모델들의 방식보다 우수함