[Paper 리뷰] Hierarchical Diffusion Models for Singing Voice Neural Vocoder

Hierarchical Diffusion Models for Singing Voice Neural Vocoder

---

• Pitch, loudness, pronunciation 같은 다양한 음악적 표현으로 인해 neural vocoder로 고품질의 가창 음성을 합성하는 것은 어려움
• 서로 다른 sampling rate에 대한 multiple diffusion model을 도입
• HPG (Hierarchical Diffusion Model + PriorGrad)
  • Lower sampling rate 모델은 pitch와 같은 저주파 요소를 합성
  • 다른 모델은 lower sampling rate와 acoustic feature를 기반으로 higher sampling rate waveform을 점진적으로 합성
• 논문 (ICASSP 2023) : Paper Link

---

1. Introduction

• Nerual vocoder는 nerual network를 사용하여 acoustic feature로부터 waveform을 생성 
  • Diffusion model은 high-fidelty sample을 합성할 수 있음
    - Denoising diffusion probabilistic model (DDPM)은 Markov chain을 활용해 istropic Gaussian dist.를 복잡한 분포로 변환
    - Forward process (=Diffusion process)는 GAN이나 VAE에서 발생하는 두 network의 joint training으로 인한 model collapse 문제를 해결 가능 
  • Neural vocoder에 diffusion model을 적용하면 고품질의 음성 데이터를 얻을 수 있지만, non-autoregressive vocoder에 비해 추론 속도가 느림
    - PriorGrad는 mel-spectrogram의 frame-wise energy를 대각 공분산 행렬 요소로 가지는 Gaussian dist.를 data dependent prior로 사용해서 추론 속도를 향상
    - Data dependent piror의 noise가 standard Gaussian noise 보다 target waveform에 더 가깝기 때문
• BUT, 기존의 neural vocoder들은 대부분 음성 합성에 초점을 두고 있음
  • 가창 음성 합성(Singing Voice Synthesis, SVS)에 기존 vocoder를 적용하면 충분한 합성 품질을 보장하지 못함
    - 충분한 가창 음성 데이터가 부족하고, pitch, loudness 등의 음악적 표현이 더 다양하기 때문

-> 그래서 서로 다른 sampling rate에서 multiple diffusion model을 학습하는 hierarchical diffusion model을 제안

 

• Hierarchical Diffusion Model
  • Lower sampling rate와 acoustic feature에 대해 condition된 diffusion model을 병렬적으로 학습
  • 추론 과정에서 lower sampling rate에서 higher sampling rate로 데이터를 점진적으로 생성
    - Lower sampling rate에서는 정확한 pitch recovery를 위한 저주파 요소 생성에 초점
    - Higher sampling rate에 대한 diffusion model은 고주파 요소 합성을 목표로 함

< Overall of This Paper >

• 고품질 가창 음성 합성을 위한 hierarchical diffusion model 기반 nerual vocoder
• 제안된 vocoder를 PriorGrad와 결합하여 최상의 가창 음성 합성 품질을 달성

2. Prior Work

- Denoising Diffusion Probabilistic Model (DDPM)

• DDPM은 forward/reverse process 두개의 Markov chain으로 구성
• Forward process
  • Data $x_{0}$를 standard Gaussian $x_{T}$로 점진적으로 diffusion 하면,
    $q(x_{1:T} | x_{0}) = \prod^{T}_{t=1} q(x_{t}|x_{t-1})$
    - $q(x_{t} | x_{t-1}) := N(x_{t}; \sqrt{1-\beta_{t}} x_{t-1}, \beta_{t}I)$ : noise schedule $\beta_{t} \in \{\beta_{1}, ..., \beta_{T} \}$을 기반으로 small Gaussian noise를 추가한 time-step $t$에서의 전이확률
  • 이때, $x_{0}$에서 $x_{t}$를 직접 sampling하면,
    $x_{t} = \sqrt{\bar{\alpha}_{t}}x_{0} + \sqrt{(1-\bar{\alpha}_{t})}\epsilon$
    - $\alpha_{t} = 1-\beta_{t}$, $\bar{\alpha}_{t} = \prod^{t}_{s=1} \alpha_{s}$, $\epsilon \sim N(0,I)$
• Reverse process
  • Prior noise $p(x_{T}) = N(x_{T};0,I)$를 data로 점진적으로 변환하면,
    $p(x_{0:T}) = p(x_{T})\prod^{T}_{t=1} p_{\theta}(x_{t-1}|x_{t})$
    - $p_{\theta}(x_{t-1}|x_{t}) := N(x_{t-1};\mu_{\theta}(x_{t},t), \sigma^{2}_{\theta}(x_{t},t)I)$ : $\theta$로 parameterize된 neural network로부터 모델링 된 $q(x_{t}|x_{t-1})$의 reverse에 대한 전이확률
  • 이때, $p_{\theta}(x_{t-1}|x_{t})$를 아래와 같이 나타내면,
    $\mu_{\theta}(x_{t}, t) = \frac{1}{\sqrt{\alpha_{t}}}(x_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \epsilon_{\theta}(x_{t},t))$
    - $\sigma^{2}_{\theta}(x_{t},t) = \frac{1-\bar{\alpha}_{t-1}} {1-\bar{\alpha}_{t}}\beta_{t}$
    - $\epsilon_{\theta}(x_{t},t)$ : time $t$에 추가된 noise $\epsilon$을 예측하는 neural network

• DDPM 최적화
  • Model $\epsilon(x_{t},t)$를 ELBO를 maximize 하는 것으로 최적화하면,
    $ELBO = C - \sum^{T}_{t=1} \kappa_{t} E_{x_{0}, \epsilon} [ || \epsilon - \epsilon_{\theta}(x_{t}, t) ||^{2} ]$
    - $C$ : 상수
    - $t > 1$일 때 $\kappa_{t} = \frac{\beta_{t}} {2 \alpha (1-\bar{\alpha}_{t-1})}$, $t=1$일 때 $\frac{1}{2\alpha}$
    - $\kappa_{t}=1$로 설정하여 단순화된 loss를 활용할 수도 있음
  • Acoustic feature $c$에 대한 noise estimation network를 $\epsilon_{\theta}(x_{t},c,t)$로 conditioning 하여 neural vocoder로써 사용
  • DDPM vocoder는 prior $x_{T}$에서 sampling 된 noise에서 시작하여 condition $c$에 기반해 신호 $x_{t}$의 noise를 반복적으로 denoise 하여 waveform $x_{0}$를 얻음

- PriorGrad

• DDPM의 standard Gaussian prior는 target data에 대한 대한 가정을 사용하지 않음
  • 고품질의 data를 얻기 위해서 많은 단계를 필요로 하므로 효율적인 추론을 방해함
  • Neural vocoder의 추론 효율성 향상을 위해 PriorGrad의 adaptive prior $N(0, \Sigma_{c})$를 사용
    - $\Sigma_{c}$ : mel-spectrogram $c$에서 $\Sigma_{c} = diag[(\sigma^{2}_{0}, ..., \sigma^{2}_{L})]$로 계산되는 diagonal variance
    - $\sigma^{2}_{i}$ : mel-spectrogram의 $i$번째 sample의 normalized frame-level energy
  • 이때, loss function은 다음과 같이 수정될 수 있음
    $L = E_{x_{0,\epsilon,t}} [ || \epsilon - \epsilon_{\theta}(x_{t},c,t)||^{2}_{\Sigma^{-1}} ]$
    - $|| x ||^{2}_{\Sigma^{-1}} = x^{t}\Sigma^{-1}x$
  • Adaptive prior의 power envelope가 standard Gaussian prior의 target 신호의 power envelope보다 가깝기 때문에 diffusion model이 더 빠르게 수렴할 수 있음

3. Proposed Method

- Hierarchical Diffusion Probabilistic Model

• PriorGrad는 음성 데이터에서는 효과적이지만 가창 음성에 대해서는 합성 품질이 떨어짐
  • Pitch, loudness, vibrato, falestto와 같은 음악적 표현 때문
  • 가창 음성을 multiple resolution으로 모델링하는 diffusion-based neural vocoder를 활용

PriorGrad와 결합한 Hierarchical Diffusion Model의 개요

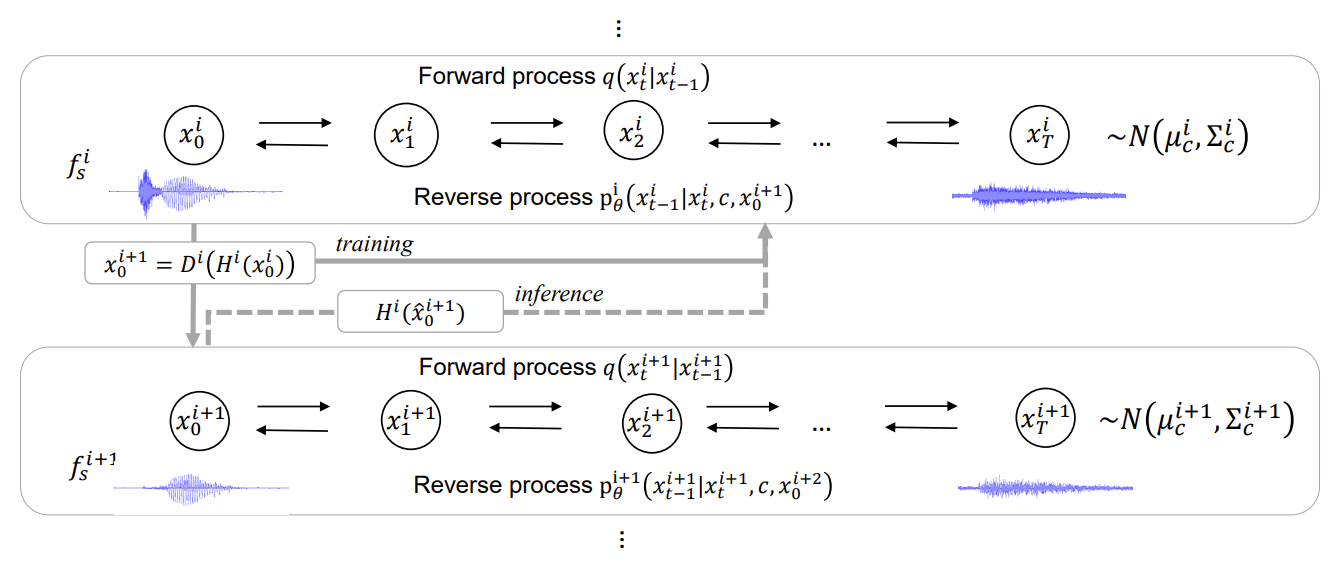
• Hierarchical Diffusion Model
  • Multiple sampling rate $f^{1}_{s} > f^{2}_{s} > ... > f^{N}_{s}$가 주어지면, Hierarchical Diffusion Model은 각 sampling rate에 대해 독립적으로 학습됨
  • 각 sampling rate $f^{i}_{s}$에 대한 reverse process는, common acoustic feature $c$과 lowest sampling rate의 model을 제외한 나머지 lower sampling rate $f^{i+1}_{s}$의 data에 대해서 condition
    $p^{i}_{\theta}(x^{i}_{t-1} | x^{i}_{t}, c, x^{t+1}_{0})$
    - Lowest sampling rate는 $c$에 대해서만 condition
• Training 단계에서,
  
  • Noise estimation model $\epsilon^{i}_{\theta}(x^{i}_{t}, c, x^{i+1}_{0}, t)$를 condition 하기 위해 ground truth $x^{i+1}_{0} = D^{i}(H^{i}(x^{i}_{0}))$을 사용
    - $H^{i}(.)$ : anti-aliasing filter, $D^{i}(.)$ : $f^{i}_{s}$ sampling rate에서 신호에 대한 downsampling function
  • Noise $\epsilon$은 original data $x_{0}$에 linear 하게 추가되므로, 모델은 ground truth lower-sampling rate data $x^{i+1}_{0}$에 직접적으로 access 할 수 있음
  • 복잡한 feature-to-waveform 변환을 피함으로써 model이 $x^{i}_{t}$와 $x^{i+1}_{0}$의 저주파 구성 요소에 대한 noise를 간단하게 예측
    - Model이 저주파 요소 대신 고주파 요소 변환에 집중하도록 유도
• Inference 단계에서, 
  • Lowest sampling rate $\hat{x}^{N}_{0}$에서 부터 data를 생성하고, 생성된 sample $\hat{x}^{i+1}_{0}$을 condition으로 하여 점진적으로 higher sampling rate $\hat{x}^{i}$에서 data를 생성
  • $x^{i+1}_{0}$을 condition으로 사용하면, 각 sampling rate $\frac{f^{2}_{s}}{2}, ..., \frac{f^{N}_{s}}{2}$의 Nyquist frequency 주변에 noise가 생성됨
  • Training과 Inference의 차이 때문:
    1. Training에 사용된 ground truth data $x^{i+1}_{0} = D^{i}(H^{i}(x^{i}_{0}))$
       - Anti-aliasing filter로 인해 Nyquist frequency 주변의 신호를 포함하지 않음
       - 결과적으로 model은 Nyquist frequency까지의 신호를 사용할 수 있는 방법을 학습함
    2. Inference에 사용된 generated sample $\hat{x}^{i+1}_{0}$
       - 불완전한 예측으로 인해 Nyquist frequency 주변의 신호를 포함할 수 있음
       - 결과적으로 higher sampling rate의 예측을 오염시킴

Anti-aliasing filter의 효과

• Nyquist frequency 문제의 해결
  • Generated lower sampling rate signal에 anti-aliasing filter를 적용해 noise prediction model을 conditioning
    $\hat{\epsilon} = \epsilon^{i}_{\theta} ( x^{i}_{t}, c, H(\hat{x}^{i+1}_{0}), t)$
  • 결과적으로 Nyquist frequency 주변의 noise를 제거하여 합성 품질을 향상

PriorGrad를 결합한 Hierarchical Diffusion Model의 Training, Inference 단계

- Network Architecture

• DiffWave에 기반한 architecture
  • Bidrectional dilated convolution과 repeated dilation factor를 가지는 $L$개의 residual layer
    - Layer는 $m$개의 block으로 그룹화
    - 각 block은 dilation factor가 $[1,2, ..., 2^{l-1}]$인 $l=\frac{L}{m}$개의 layer로 구성
  • 모든 sampling rate에 대해 동일한 network architecture를 사용하면 sampling rate에 따라 model의 recpetive field가 변화함
    - Sampling rate가 낮을수록 model은 더 긴 기간을 포함하고, 저주파 요소에 집중함
    - Nyquist frequency $\frac{f^{i+1}_{s}}{2}$까지는 lower sampling rate $x^{i+1}_{0}$으로 condition 된 data를 사용하고 고주파 영역에 대해서는 acoustic feature를 변환할 수 있도록 만듦

서로 다른 sampling rate에서의 receptive field 변화

4. Experiments

- Settings

• Dataset : NUS48E, NHSS
• Comparisons : PriorGrad, Parallel WaveGAN (PWG)

- Results

• 제안한 방식이 가장 높은 MOS 품질을 달성
  - 가창 음성에 vibrato가 있는 경우에도 제안한 방식은 부자연스러운 pitch를 생성하지 않기 때문
  - 합성된 가창 음성에 대한 선호도 평가에서도, 제안한 방식이 85.3%의 선호도를 보임

MOS 기반 주관적 가창 음성 품질 평가

• PMAE, VDE, MR-STFT, MCD 등에 대한 객관적인 품질 평가에 대해서도, 제안한 방식이 가장 좋은 성능을 보임

객관적인 품질 평가

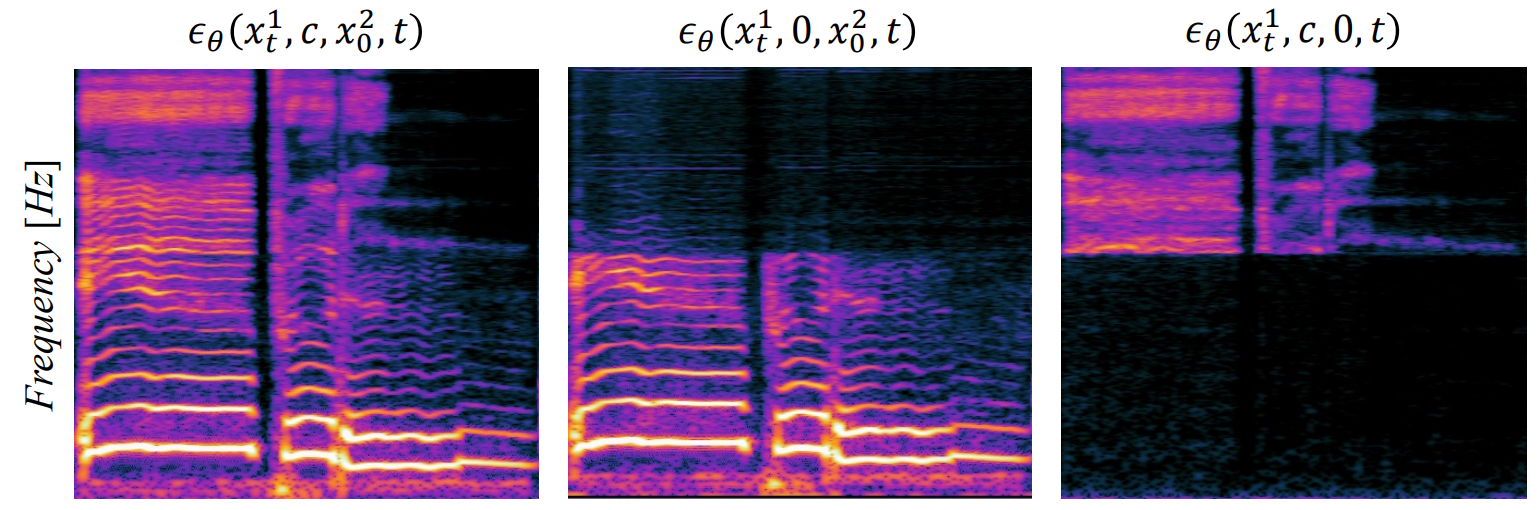
• 제안한 방식이 conditioning data를 어떻게 활용하는지 조사
  • Mel-spectrogram을 0으로 대체하더라도 Nyquist frequency $\frac{f^{2}_{s}}{2}$에 대한 신호를 생성가능
  • Lower sampling rate data $x^{2}_{0}$를 0으로 대체하면, 고주파 영역의 신호만 생성
    - 저주파 영역 생성 시 $x^{2}_{0}$의 정보가 사용되고, 고주파 영역은 $c$에 의해서 생성됨

서로 다른 conditioning으로 생성된 mel-spectrogram 비교