[Paper 리뷰] DPHuBERT: Joint Distillation and Pruning of Self-Supervised Speech Models

DPHuBERT: Joint Distillation and Pruning of Self-Supervised Speech Models

---

• Self-supervised learning은 model size와 computation cost 측면에서 한계가 있음
• DPHuBERT
  • Knowledge Distillation과 task-specific Structured Pruning을 통해 self-supervised model을 compress
  • 결과적으로 resource-constrained application에서 pure-distillation method 보다 우수한 성능을 달성
• 논문 (INTERSPEECH 2023) : Paper Link

---

1. Introduction

• Wav2Vec 2.0, HuBERT, WavLM과 같은 speech representation에 대한 Self-Supervised Learning (SSL)은 resource size로 인해 real-world application에서 활용하기 어려움
  • 이때 DistilHuBERT와 같이 Knowledge Distillation을 사용하면 large teacher로부터 small student를 얻을 수 있음
    - BUT, distillation은 student architecture가 pre-specify 되므로 suboptimal result가 발생할 수 있음
  • 한편으로 pruning을 통해 large model에서 compacy sub-network를 얻을 수도 있음

-> 그래서 Distillation과 Pruning을 사용해 speech SSL model을 compress 한 DPHuBERT를 제안

 

• DPHuBERT
  • Task-agnostic compression을 위해 Distillation과 Pruning을 결합
  • HuBERT, WavLM과 같은 다양한 speech SSL model에 적용 가능

< Overall of DPHuBERT >

• Distillation과 Pruning을 사용한 speech SSL model
• 결과적으로 더 적은 training resource를 사용하면서 기존 수준의 성능을 달성 가능

2. Method

- Training Procedure

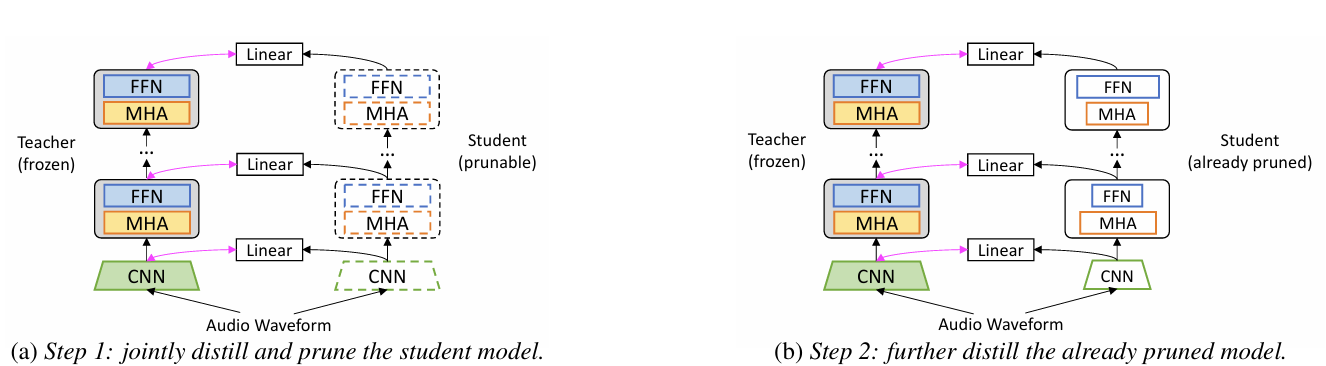
• DPHuBERT의 training procedure는 2-step으로 구성됨 
  1. 먼저 student model은 teacher로부터 initialize 되고 pre-specified size로 smaller model을 생성하기 위해 jointly distill, pruning 됨 
  2. 이후 pruned student model은 성능 향상을 위해 further distill 됨 
     - 모든 step에서 unlabeled speech data만 사용되고, teacher는 frozen 됨

Training Procedure

- Distillation Loss

• DistilHuBERT와 달리 student가 처음에는 teacher와 동일한 depth를 가지므로 layer-to-layer distillation을 사용함
  • 먼저 teacher가 hidden size $d^{tea}$의 $N^{tea}$ Transformer layer를 가지고, student는 hidden size $d^{stu}$의 $N^{stu}$ layer를 가진다고 하자 
    1. $T\times d^{tea}$ shape의 $\mathbf{X}^{tea}_{i}$와 $T\times d^{stu}$ shape의 $\mathbf{X}_{i}^{stu}$를 각각 teacher/student의 $i$-th Transformer layer output sequence라고 할 때,
       - $T$ : sequence length
    2. Distillation loss는: 
       (Eq. 1) $ \mathcal{L}^{dis}=\sum_{i\in\mathcal{S}}\mathcal{L}(\mathbf{W}_{i}^{tea},\mathbf{W}_{i}^{stu}\mathbf{W}_{i})$
       - $\mathcal{S}$ : linear projection $\mathbf{W}_{i}$ 이후 teacher, student 간에 match 할 layer set
       - $\mathcal{S}=\{0,4,8,12\}$ : base model, $\mathcal{S}=\{0,8,16,24\}$ : large model
  • 여기서 0-th layer는 CNN output으로써 first Transformer layer의 input이고, loss function $\mathcal{L}$은 두 feature sequence 간의 difference를 얻기 위해 $L_{1},L_{2}$, cosine distance를 사용할 수 있음
    - 논문은 DistilHuBERT를 따라 $L_{1}$과 cosine distance를 equal weight로 combine 하여 사용함

- Joint Distillation and Structured Pruning

• Student model에 대한 structured pruning은 $L_{0}$ regularization을 통해 sparse model을 학습하는 것으로 formulate 됨
  • 먼저 frozen teacher model $f^{tea}(\cdot)$과 learnable parameter $\boldsymbol{\theta}=\{\theta_{j}\}_{j=1}^{n}$을 가지는 student model $f^{stu}(\cdot;\boldsymbol{\theta})$가 있다고 하자
    1. 각 $\theta_{j}$는 prunable parameter (convolution channel, attention head, FFN intermediate unit)의 group으로써 총 $n$ group을 가짐
    2. 그러면 각 $\theta_{j}$에 대한 mask로써 binary variable $z_{j}$를 정의할 수 있음
       - Mask $\mathbf{z}$는 parmaeter $\boldsymbol{\alpha}$에 대한 probability distribution $q(\mathbf{z};\boldsymbol{\alpha})$를 따름
    3. 결과적으로 얻어지는 regularized distillation objective는:
       (Eq. 2) $\min_{\boldsymbol{\theta},\boldsymbol{\alpha}}\mathbb{E}_{\mathbf{z}\sim q}\left[\frac{1}{D}\sum_{k=1}^{D} \mathcal{L}^{dis}\left( f^{tea}(\mathbf{x}_{k}), f^{\text{stu}}(\mathbf{x}_{k};\tilde{\boldsymbol{\theta}})\right)+\lambda || \tilde{\boldsymbol{\theta}}||_{0}\right]$
       - $\tilde{\boldsymbol{\theta}}=\{\tilde{\theta}\}_{j=1}^{n}$이고 각 $\tilde{\theta}_{j} =\theta_{j}z_{j}$ 
       - $\{\mathbf{x}_{k}\}_{k=1}^{D}$ : $D$ sample을 가지는 unlabeled dataset
       - $\lambda>0$ : regularization weight
  • 한편으로 mask $\mathbf{z}$의 discrete nature로 인해 (Eq. 2)를 gradient descent로 solve 하는 것은 intractable 함
    1. 따라서 differentiable loss를 얻기 위해, Hard Concrete distribution $\mathbf{z}$에서 sampling을 수행하는 reparameterization trick을 활용함:
       (Eq. 3) $\mathbf{u}\sim\mathcal{U}(0,1),\,\, \mathbf{v}(\boldsymbol{\alpha})=\text{sigmoid}\left( \left( \log \frac{\mathbf{u}}{1-\mathbf{u}}+\log \boldsymbol{\alpha}\right)/\beta\right)$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \bar{\mathbf{v}}(\boldsymbol{\alpha})=(r-l)\cdot\mathbf{v}(\boldsymbol{\alpha})+l,\,\,\mathbf{z}= \min\left(1,\max(0,\bar{\mathbf{v}}(\boldsymbol{\alpha}))\right) $
       - $\mathbf{u}$ : $[0,1]$의 uniform distribution을 따르는 값, $\beta$ : constant
       - $l<0, r>0$ : $\mathbf{v}$를 $[l,r]$로 stretch 하기 위한 constant로써 $[0,1]$로 further clamp 됨
       - $\boldsymbol{\alpha} =\{\alpha_{j}\}_{j=1}^{n}$ : learnable parameter
    2. 해당 trick 하에서 (Eq. 2)의 objective는 differentiable 하고 closed-form의 regularization term을 가짐:
       (Eq. 4) $\mathbb{E}_{\mathbf{z}\sim q}\left[|| \tilde{\boldsymbol{\theta}}||_{0}\right]=\sum_{j=1}^{n}\text{sigmoid}\left( \log \alpha_{j}-\beta \log \frac{-l}{r}\right)$
       - 이는 expected model size를 current parameter $\boldsymbol{\alpha}$의 differentiable function으로 represent 함
  • (Eq. 2)는 sparse subnet을 학습하는 것으로 solve 될 수 있지만, final sparsity는 precisely control 할 수 없음
    1. 이때 final model size를 explicitly control 하기 위해서는 equality constraint로 optimization problem을 다음과 같이 rewrite 해야 함:
       (Eq. 5) $\min_{\boldsymbol{\theta},\boldsymbol{\alpha}}\mathbb{E}_{\mathbf{z}\sim q}\left[\frac{1}{D}\sum_{k=1}^{D} \mathcal{L}^{dis}\left( f^{tea}(\mathbf{x}_{k}),f^{stu}(\mathbf{x}_{k};\tilde{\boldsymbol{\theta}})\right)\right],\,\,\, \text{s.t.}\,\, s(\boldsymbol{\alpha})=t$
       - $s(\boldsymbol{\alpha})$ : student model의 current sparsity (pruned parameter의 percentage)
       - $t$ : pre-specified target sparsity
    2. $s(\boldsymbol{\alpha})$는 $L_{0}$ norm이 remaining parameter를 count 하므로 (Eq. 4)를 통해 compute 됨
    3. (Eq. 5)의 optimization objective는 augmented Lagrangian을 통해 minmax problem으로 further convert 됨:
       (Eq. 6) $\max_{\lambda_{1},\lambda_{2}}\min_{\boldsymbol{\theta},\boldsymbol{\alpha}}\mathbb{E}_{\mathbf{z}\sim q}\left[\frac{1}{D}\sum_{k=1}^{D}\mathcal{L}^{dis}\left( f^{tea}(\mathbf{x}_{k}), f^{stu}(\mathbf{x}_{k},\tilde{\boldsymbol{\theta}})\right)\right]+\lambda_{1}\cdot (s(\boldsymbol{\alpha})-t)+\lambda_{2}\cdot (s(\boldsymbol{\alpha})-t)^{2}$
       - $\lambda_{1},\lambda_{2}\in\mathbb{R}$ : Lagrange multiplier
  • (Eq. 6)의 additional term은 distillation loss를 penalize 하고 student model이 target sparsity를 만족하도록 함
    - 결과적으로 training procedure의 Step 1은 (Eq. 6)을 training objective로 사용하고, Step 2는 constraint 없이 (Eq. 1)의 distillation loss를 objective로 사용함 

3. Experiments

- Settings

• Dataset : LibriSpeech
• Comparisons : Wav2Vec 2.0, HuBERT, WavLM, DistilHuBERT, FitHuBERT

- Results

• 전체적으로 DPHuBERT의 성능이 가장 우수함

성능 비교

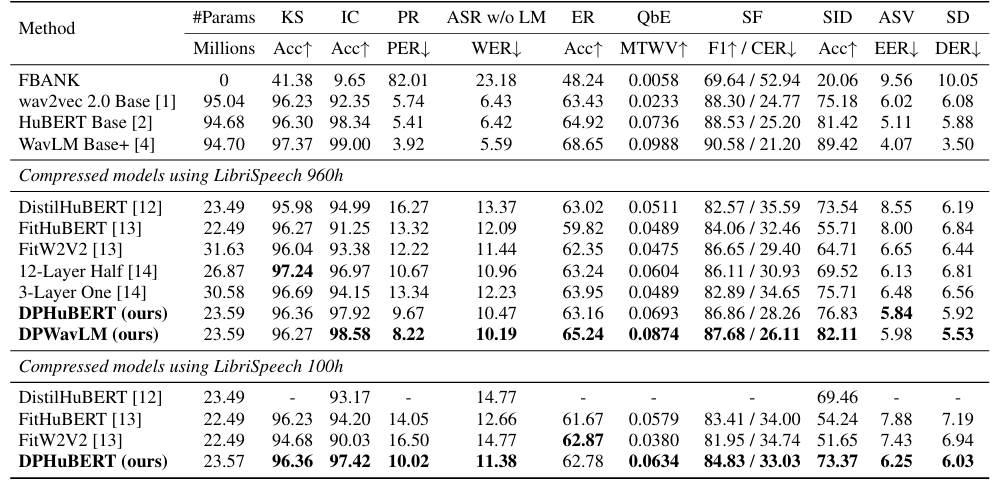
• Architecture 측면에서 first/last CNN layer가 가장 많이 pruning 되고, MHA의 경우 3개의 higher layer가 remove 됨
  - FFN의 경우, 4,8,12-th layer가 가장 많이 preserve 됨

Compressed Architecture

• Ablation Study
  • 각 component를 제거하는 경우 성능 저하가 발생함

Ablation Study

• Results at Various Sparsities
  • (Eq. 5), (Eq. 6)의 target sparsity $t$ 측면에서, DPHuBERT는 기존 수준의 성능을 유지하면서 model size를 더 reduce 할 수 있음

Sparsity의 영향

• Compressing HuBERT-Large
  • DPHuBERT는 HuBERT-Large를 HuBERT-Base와 비슷한 size로 compress 할 수 있음

HuBERT-Large Compressing