티스토리 뷰
Paper/Representation
[Paper 리뷰] VQ-Wav2Vec: Self-Supervised Learning of Discrete Speech Representations
feVeRin 2025. 4. 25. 17:53반응형
VQ-Wav2Vec: Self-Supervised Learning of Discrete Speech Representations
- Wav2Vec-style self-supervised context prediction을 통해 audio segment의 discrete representation을 학습할 수 있음
- VQ-Wav2Vec
- Gumbel-Softmax, online $k$-means clusetering을 활용하여 dense representation을 quantize
- Discretization을 통해 BERT pre-training을 directly applicate
- 논문 (ICLR 2020) : Paper Link
1. Introduction
- Discrete speech representation을 학습하기 위해서는 autoencoding이나 autoregressive model을 주로 활용함
- 한편으로 continuous speech representation 학습을 위해서는 context information을 predict 함
- 이를 위해 Speech2Vec, Wav2Vec 등이 사용됨
-> 그래서 context prediction을 기반으로 discrete speech representation을 학습하는 VQ-Wav2Vec을 제안
- VQ-Wav2Vec
- Wav2Vec architecture를 활용하여 audio signal의 fixed length segment에 대한 discrete representation을 학습
- Discrete variable을 choice 하기 위해 Gumbel-Softmax와 $k$-means clustering을 채택
- 추가적으로 discretized unlabeled speech data로 BERT를 training 한 다음, 해당 representation을 standard acoustic model에 input
< Overall of VQ-Wav2Vec >
- Wav2Vec와 quantization method를 활용해 학습되는 discrete speech representation
- 결과적으로 다양한 benchmark에서 기존보다 우수한 성능을 달성
2. Background
- Wav2Vec
- Wav2Vec은 self-supervised context-prediction task를 활용하여 audio representation을 학습함
- 구조적으로는 2개의 convolution neural network를 기반으로 함
- 여기서 encoder는 100Hz rate로 각 time step $i$에 대한 representation $\mathbf{z}_{i}$를 생성함
- Aggregator는 multiple encoder time step을 각 time step $i$에 대한 new representation $\mathbf{c}_{i}$로 combine 함
- Aggregated reprsentation $\mathbf{c}_{i}$가 주어지면, step $k=1,...,K$에 대한 contrastive loss를 minimize 하여 future $k$ step의 sample $\mathbf{z}_{i+k}$를 distribution $p_{n}$에서 추출한 distractor sample $\tilde{\mathbf{z}}$와 distinguish 하도록 training 됨:
(Eq. 1) $ \mathcal{L}_{k}^{\text{wav2vec}}=-\sum_{i=1}^{T-k}\left( \log \sigma\left( \mathbf{z}_{i+k}^{\top}h_{k}(\mathbf{c}_{i})\right)+\lambda\mathbb{E}_{\tilde{\mathbf{z}}\sim p_{n}}\left[ \log \sigma\left(-\tilde{\mathbf{z}}^{\top}h_{k}(\mathbf{c}_{i})\right)\right]\right)$
- $T$ : sequence length, $\sigma(x)=1/(1+\exp(-x))$
- $\sigma\left(\mathbf{z}_{i+k}^{\top}h_{k}(\mathbf{c}_{i})\right)$ : $\mathbf{z}_{i+k}$가 true sample일 probability - 여기서 논문은 $\mathbf{c}_{i}$에 적용되는 step-specific affine transformation $h_{k}(\mathbf{c}_{i})=W_{k}\mathbf{c}_{i}+\mathbf{b}_{k}$을 고려하고, loss $\mathcal{L}=\sum_{k=1}^{K}\mathcal{L}_{k}$를 optimize 하여 서로 다른 step size에 대해 (Eq. 1)을 summation 함
- Training 이후 context network에 의해 생성된 representation $\mathbf{c}_{i}$는 log-mel filterbank feature를 대체하여 acoustic model에 input 됨
- 구조적으로는 2개의 convolution neural network를 기반으로 함
3. Method
- VQ-Wav2Vec은 future time-step prediction task를 사용하여 audio data의 Vector Quantized (VQ) representation을 학습함
- 이를 위해 Wav2Vec과 동일한 architecture를 기반으로 feature extraction, aggregation을 수행하는 2개의 convolution network $f:\mathcal{X}\mapsto \mathcal{Z},g:\hat{\mathcal{Z}}\mapsto \mathcal{C}$를 도입함
- 추가적으로 quantization module $q:\mathcal{Z}\mapsto \hat{\mathcal{Z}}$을 통해 discrete representation을 build 함 - 먼저 논문은 encoder network $f$를 사용하여 30ms segment의 raw speech를 10ms stride로 dense feature representation $\mathbf{z}$에 mapping 함
- 이후 quantizer $q$는 dense representation을 original representation $\mathbf{z}$의 reconstruction $\hat{\mathbf{z}}$에 mapping되는 discrete index로 변환함
- 최종적으로 $\hat{\mathbf{z}}$를 aggregator $g$에 전달하여 Wav2Vec과 동일한 context prediction task를 optimize 함
- Quantization module은 $d$ size의 $V$ representation을 포함하는 fixed size codebook $\mathbf{e}\in\mathbb{R}^{V\times d}$의 original representation $\mathbf{z}$를 $\hat{\mathbf{z}}=\mathbf{e}_{i}$로 replace 함
- 이때 논문은 one-hot representation을 computing 하기 위해, argmax의 differentiable approximation인 Gumbel-Softmax와 online $k$-menas clustering를 고려함
- 추가적으로 mode collapse를 방지하기 위해 $\mathbf{z}$의 different part에 대해 multiple vector quantization을 수행함
- 이때 논문은 one-hot representation을 computing 하기 위해, argmax의 differentiable approximation인 Gumbel-Softmax와 online $k$-menas clustering를 고려함
- 이를 위해 Wav2Vec과 동일한 architecture를 기반으로 feature extraction, aggregation을 수행하는 2개의 convolution network $f:\mathcal{X}\mapsto \mathcal{Z},g:\hat{\mathcal{Z}}\mapsto \mathcal{C}$를 도입함

- Gumbel-Softmax
- Gumbel-Softmax를 사용하면 fully differentiable way로 discrete codebook variable을 select 할 수 있으므로, 논문은 straight-through estimator를 채택함
- Dense representation $\mathbf{z}$가 주어졌을 때, 논문은 linear layer, ReLU를 적용하고 Gumbel-Softmax logit $\mathbf{l}\in\mathbb{R}^{V}$를 output 하는 another linear layer를 도입함
- Inference 시에는 $l$의 largest index를 picking 함 - Training 시 $j$-th variable을 choice 하는 output probability는:
(Eq. 2) $p_{j}=\frac{\exp\left(l_{j}+v_{j}\right)/\tau}{\sum_{k=1}^{V}\exp\left(l_{k}+v_{k}\right)\tau}$
- $v=-\log (-\log (u))$, $u$ : $\mathcal{U}(0,1)$의 uniform sample - Forward pass에서는 $i=\arg\max_{j}p_{j}$를 사용하고, backward pass에서는 Gumbel-Softmax output의 true gradient가 사용됨
- Dense representation $\mathbf{z}$가 주어졌을 때, 논문은 linear layer, ReLU를 적용하고 Gumbel-Softmax logit $\mathbf{l}\in\mathbb{R}^{V}$를 output 하는 another linear layer를 도입함

- $K$-Means
- 논문은 autoencoder reconstruction loss 대신 future time step prediction loss를 optimize 함
- 이때 Euclidean distance 측면에서 input feature $\mathbf{z}$에 대한 closest variable을 find 하여 codebook variable representation을 choice 하고 $i=\arg\min_{j}|| \mathbf{z}-\mathbf{e}_{j}||_{2}^{2}$를 yield 함
- Forward pass 시에는 codebook에서 해당 variable을 choice 하여 $\hat{\mathbf{z}}=\mathbf{e}_{i}$를 select 하고, $\text{d}\mathcal{L}^{\text{wav2vec}}/\text{d}\hat{\mathbf{z}}$를 backpropagate 하여 encoder network에 대한 gradient를 얻음
- 그러면 final loss는:
(Eq. 3) $\mathcal{L}=\sum_{k=1}^{K}\mathcal{L}_{k}^{\text{wav2vec}}+\left(|| \text{sg}(\mathbf{z})-\hat{\mathbf{z}}||^{2}+\gamma || \mathbf{z}-\text{sg}(\hat{\mathbf{z}})||^{2}\right)$
- $\text{sg}(x)\equiv x,\frac{\text{d}}{\text{d}x}\text{sg}(x)\equiv 0$ : stop-gradient operator, $\gamma$ : hyperparameter
- (Eq. 3)에서 first term은 future prediction task이고 gradient는 $\mathbf{z}$를 $\hat{\mathbf{z}}$에 mapping 하는 straight-through gradient estimation이므로 codebook을 변경하지 않음
- Second term $|| \text{sg}(\mathbf{z})-\hat{\mathbf{z}}||^{2}$는 codebook vector를 encoder output에 close 하고, third term $|| \mathbf{z}-\text{sg}(\hat{\mathbf{z}})||^{2}$은 encoder output이 centroid (codeword)에 close 하도록 함
- 이때 Euclidean distance 측면에서 input feature $\mathbf{z}$에 대한 closest variable을 find 하여 codebook variable representation을 choice 하고 $i=\arg\min_{j}|| \mathbf{z}-\mathbf{e}_{j}||_{2}^{2}$를 yield 함
- Vector Quantization with Multiple Variable Groups
- Codebook의 single entry $\mathbf{e}_{i}$로 encoder feature vector $\mathbf{z}$를 replace 하면 codeword의 일부만 사용하는 mode collapse가 발생할 수 있음
- 따라서 논문은 product quantization과 유사하게 $\mathbf{z}$의 partition을 independently quantize 하여 downstream performance를 향상함
- 먼저 dense feature vector $\mathbf{z}\in\mathbb{R}^{d}$는 multiple group $G$로 구성되어 matrix $\mathbf{z}'\in\mathbb{R}^{G\times (d/G)}$를 구성함
- 여기서 각 row는 integer index를 represent 하므로 index $\mathbf{i}\in[V]^{G}$로 full feature vector를 represent 할 수 있음
- $V$ : particular group에 대해 possible variable 수, $\mathbf{i}_{j}$ : fixed codebook vector - 이후 각 $G$ group에 대해 Gumbel-Softmax나 $k$-means를 적용함
- 여기서 각 row는 integer index를 represent 하므로 index $\mathbf{i}\in[V]^{G}$로 full feature vector를 represent 할 수 있음
- Codebook은 다음의 2가지 방법으로 initialize 될 수 있음:
- 먼저 codebook variable은 group 간에 share 될 수 있으므로, group $j$의 particular index는 group $j'$의 same index, same vector를 reference 함
- 이를 통해 codebook $\mathbf{e}\in\mathbb{R}^{V\times (d/G)}$가 얻어짐 - Codebook variable을 share 하지 않는 경우, codebook $\mathbf{e}\in\mathbb{R}^{V\times G\times (d/G)}$을 얻을 수 있음
- 경험적으로 codebook sharing을 채택하면 더 나은 결과를 얻을 수 있음
- 먼저 codebook variable은 group 간에 share 될 수 있으므로, group $j$의 particular index는 group $j'$의 same index, same vector를 reference 함
4. BERT Pre-Training on Quantized Speech
- VQ-Wav2Vec이 training 되면 audio data를 discretize 하여 discrete input이 필요한 algorithm에 적용할 수 있음
- 대표적으로 discretized training data를 기반으로 surrounding context encoding을 통해 masked input token을 predict 하는 BERT pre-training에 사용될 수 있음
- 특히 해당 trained BERT model을 통해 representation을 build 하고 acoustic model에 전달하여 speech recognition 성능을 향상할 수 있음 - 한편으로 discretized token은 10ms audio를 represent 하므로 단순히 single masked input token을 predict 하는 것은 너무 쉬움
- 따라서 논문은 consecutive discretized speech token span을 masking 하는 방식으로 BERT training을 변경함
- Input sequence를 masking 하기 위해 모든 token을 $p=0.05$로 randomly sample 하여 starting index로 설정하고, $M=10$ consecutive token을 각 sampled index 마다 mask 함 - 이는 masked token prediction을 어렵게 만들어 individual token masking 보다 accuracy를 향상함
- 따라서 논문은 consecutive discretized speech token span을 masking 하는 방식으로 BERT training을 변경함
- 대표적으로 discretized training data를 기반으로 surrounding context encoding을 통해 masked input token을 predict 하는 BERT pre-training에 사용될 수 있음
5. Experiments
- Settings
- Dataset : LibriSpeech, TIMIT, WSJ
- Comparisons : Wav2Vec
- Results
- WSJ Speech Recognition
- WSJ benchmark에 대해 VQ-Wav2Vec이 가장 우수한 성능을 달성함

- LM을 사용하지 않는 경우 Gumbel-Softmax가 $k$-means 보다 우수하지만, 4-gram LM의 경우 $k$-means가 더 나은 성능을 보임

- TIMIT Phoneme Recognition
- TIMIT task에 대해서도 VQ-Wav2Vec은 뛰어난 성능을 보임

- Sequence to Sequence Modeling
- VQ-Wav2Vec은 data augmentation 없이도 Sequence to Sequence modeling에서 reasonable한 성능을 달성함

- Accuracy vs. Bitrate
- VQ-Wav2Vec은 대부분의 bitrate setting에서 뛰어난 PER을 달성함

- Ablations
- Token의 entire span을 mask 하면 individual token을 mask 하는 것보다 더 나은 성능을 달성할 수 있음
- Discretized audio data에 대한 BERT training은 input masking에 대해 fairly robust 함
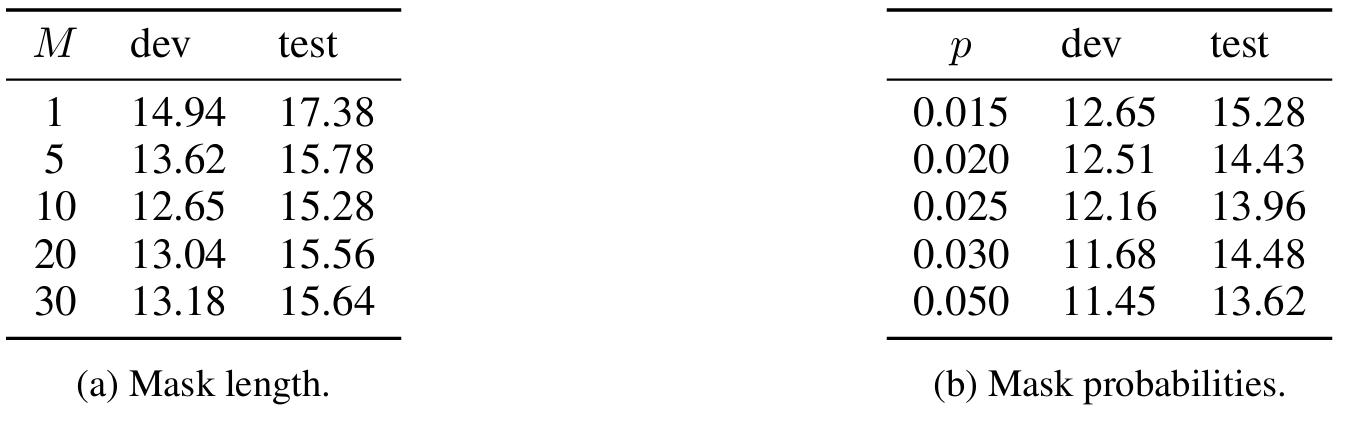
반응형
'Paper > Representation' 카테고리의 다른 글
댓글

