[Paper 리뷰] Fast and Accurate Model Scaling

Fast and Accurate Model Scaling

---

• 일반적인 CNN에서 width, depth, resolution 등을 scaling 하여 더 나은 representational power를 부여할 수 있음
• 기존의 scaling 방식은 accuracy와 FLOP의 상호작용에 초점을 맞추고 있음
• Fast Compound Scaling
  
  • Scaling 전략은 parameter 수, activation, runtime에 대해 각각 다른 영향을 미침
  • Width를 확장하는 대신 depth, resolution을 더 작은 범위로 scaling 하는 fast compound scaling 방식 제시
• 논문 (CVPR 2021) : Paper Link

---

1. Introduction

• CNN은 GPU, TPU와 같은 고성능 hardware를 통해 더 크고 정확한 모델을 학습할 수 있음
  • Low-compute regime에서 이러한 hardware 발전은 최적화에 큰 도움이 되었음
  • Intermediate-compute regime에서는 효율적인 search나 design space가 도움이 될 수 있음
  • High-compute regime에는 컴퓨팅 자원에 관계없이 단일 모델만을 학습할 수 있어야함
• High-compute regime에서는 하나 이상의 차원 (depth or width)을 확장하여 복잡도가 낮은 모델을 얻을 수 있는 network scaling이 중요함
  • Scaling은 좋은 accuracy로 더 큰 모델을 얻을 수 있지만, 기존의 방식들은 accuracy에만 중점을 두고 있음
    - 실제로 배포하고, 사용할 수 있는 충분히 빠르고 정확한 (fast and accurate) 모델을 얻을 수 있어야 함
  • 대부분의 network scaling은 depth를 증가시키는 방법을 사용
    - 한 번에 여러 차원을 scaling 하는 coined compound scaling이 등장
  • 대부분의 scaling 방식은 FLOP 대비 accuracy를 최대화하는 것이 목표
    - 동일한 FLOP을 가지는 확장 모델은 acclerator에서 서로 다른 실행 시간을 가질 수 있음

-> 그래서 Accuracy와 실행 시간을 모두 최적화하는 scaling 방식을 제안

 

• Fast Compound Scaling
  • 동일한 FLOP에서 유사한 accuracy를 가지는 모델을 생성할 수 있는 여러 scaling 방법이 존재
  • 두 개의 scaling 방식을 활용해 모델을 고정된 target FLOP으로 scaling해도 서로 다른 실행 시간을 가짐
    - Width에 대해 모델을 $f$ FLOP에서 $sf$ FLOP으로 scaling 할 때 activation은 $O(s)$을 보임
    - Fast compound scaling을 활용하면 $O(\sqrt{s})$ 만큼 activation이 점근적으로 증가함
  • Accelerator에서 scaling 된 모델의 실행 시간은 FLOP보다 activation에 더 높은 상관관계를 가짐
    - Activation을 모델 실행 시간을 예측하기 위한 proxy로 사용할 수 있음

Scaling 방식에 따른 activation, 실행시간 비교

< Overall of Fast Compound Scaling >

• Width에 따라 상대적인 scaling을 제어하는 $\alpha$로 parameterize 된 scaling 방법
• 모델 activation의 점근적 증가를 제어해 $0 \ll \alpha < 1$ 범위에서 빠르고 정확한 모델을 생성 가능
• Fast compound scaling을 활용해 SOTA 모델과 비슷한 정확도를 가지면서도 더 빠른 대형 모델을 얻음

2. Complexity of Scaled Models

- Complexity Metrics

• FLOP $f$, Parameter $p$, Activation $a$ 3가지 속성에 대해 고려
  - FLOP : multiply-add를 의미
  - Parameter : 모델의 free variables 수를 의미
  - Activation : convolution layer의 output tensor에 있는 element의 수
• FLOP, Parameter는 neural network의 대표적인 복잡도 척도임
  • Convolution의 parameter는 input resolution과 무관함
    -> Convolution network의 실제 용량이나 실행시간을 반영하지 못함
  • Input resolution이 다양한 network의 경우, FLOP에 초점을 맞춤

• Activation은 memory-bandwidth 제한 hardware에서 network의 속도를 결정함
  • Scaling과 activation 간의 상호작용을 분석하는데 초점을 맞춤

- Network Complexity

• Convolution network는 많은 heterogeneous layer로 구성되어 있음
  • Convolution layer에 대한 복잡도 분석
    1. Normalization, pooling, activation은 모델 컴퓨팅 비용에서 적은 비중을 가짐
    2. Layer의 수와 복잡도는 convolution layer의 수와 크기에 비례함
  • Convolution에 대한 분석은 scaling이 전체 network에 미치는 영향에 대한 proxy의 역할을 할 수 있음
• $k \times k$ convolution layer
  • Width (channel 개수) : $w$
  • Spatial resolution : $r$
  • $r \times r \times w$ 크기의 feature map, $k \times k \times w$ 크기의 $r^{2}$ patch 각각에 대해 크기 $wk^{2}$의 $w$ 내적을 계산
  • Convolution layer의 복잡도 : $f = w^{2}r^{2}k^{2}, p = k^{2}w^{2}, a = wr^{2}$
    - $k$가 scaling 되지 않았으므로 $k=1$로 둠
• Common network는 여러 단계로 구성되고, 각 단계는 동일한 $w$와 $r$을 가지는 $d$개의 convolution layer로 구성됨
  - Depth $d$단계에 대한 복잡도 : $f = dw^{2}r^{2}, p = dw^{2}, a = dwr^{2}$

- Complexity of Simple Scaling

• 단일 차원을 따라 단계를 확장하는 것으로 simple scaling을 정의
  • Width $w$, Depth $d$, Resolution $r$에 대한 scaling을 고려
  • Scaling이 모델 FLOP을 증가시키는 양으로써 scaling factor $s$를 정의
    - $d$를 $s$, $w$를 $\sqrt{s}$, $r$을 $\sqrt{s}$로 늘릴 때 FLOP이 $s$만큼 증가함
  • FLOP은 동일하지만 parameter의 activation은 다양할 수 있음
    - Resolution이나 depth에 따라 scaling 할 때에 비해, width에 따라 scaling 하면 activation이 $\sqrt{s}$배 증가함

Simple scaling의 복잡도

- Complexity of Compound Scaling

• 단일 차원에 따라 scaling 하는 대신 한 번에 여러 차원을 scaling 하는 방법을 compound scaling으로 정의
  • Simple scaling 보다 더 높은 accuracy를 달성할 수 있음
  • 모든 차원 ($dwr$)을 따라 scaling하는 경우
    - $d$를 $\sqrt[3] {s}$, $w$를 $\sqrt[6] {s}$, $r$을 $\sqrt[6] {s}$로 scaling 하면,
    - FLOP은 각 차원마다 $\sqrt[3] {s}$만큼 증가하므로, 총 $\sqrt[3] {s}^{3} = s$만큼 증가함
  • 경험적으로 1.2, 1.1, 1.15로 $d, w, r$을 scaling 하는 것은, $s = 2(\sqrt[3]{s} \approx 1.26, \sqrt[6]{s} \approx 1.12)$인 uniform compound scaling에 해당
    - Uniform compound scaling의 경우 activation은 $s$에 따라 거의 선형적으로 증가함

Compound scaling의 복잡도

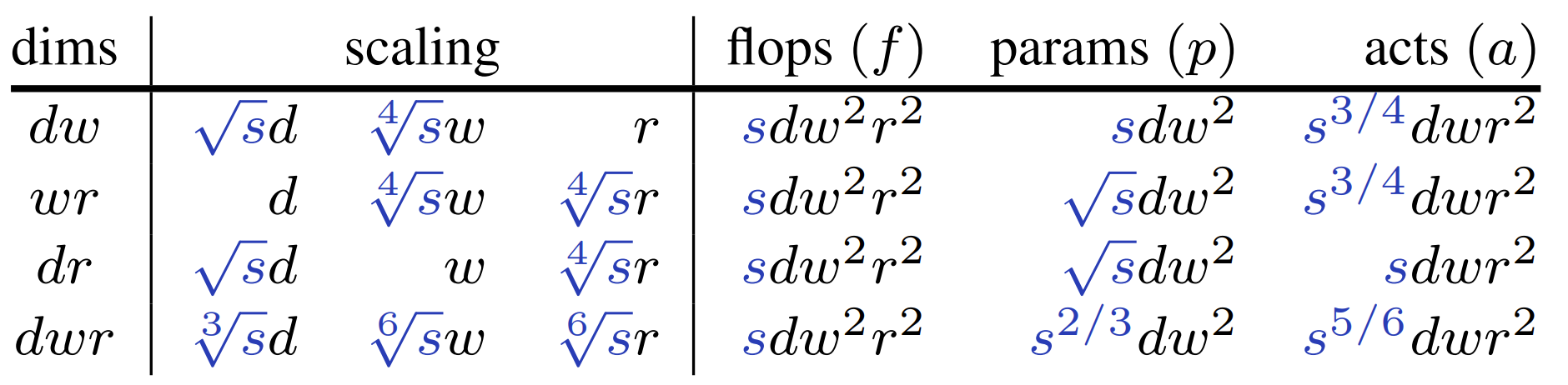
- Complexity of Group Width Scaling

• 많은 최고 성능의 network는 group convolution과 depthwise convolution에 의존
  • Channel width가 $w$이고 group width가 $g$인 group convolution
    - $w$ channel을 각 width가 $g$인 $w/g$ group으로 분할하고, 각 group에 regular convolution을 적용하여 concatenation 한 것과 동일
    - Depthwise convolution은 $g=1$인 특수한 경우로 볼 수 있음
  • Group convolution의 복잡도 : $f = wgr^{2}, p = wg, a = wr^{2}$
  • Regular convolution scaling과 동일한 scaling을 얻으려면 channel width와 group width를 모두 scaling 해야 함
    - $g$를 $w$에 비례하여 scaling
    - Depthwise convolution ($g=1$)인 경우 $g$를 scaling 하지 않음
  • $g$를 scaling 할 때 $w$를 $g$로 나눌 수 있는지 확인해야 함
    - $g>w$인 경우 $g=w$로 설정하고, 그렇지 않은 경우 $w$를 $g$로 나눌 수 있도록 반올림

Group scaling의 복잡도

3. Runtime of Scaled Models

• Complexity metric과 accelerator에서 모델 실행시간 간의 관계
  • FLOP, Parameter, Activation에 대해 실행시간을 비교
    - 단일 모델을 scaling 할 때 FLOP과 parameter 수는 실행시간을 약하게 예측함
    - Activation은 scaling 방식에 관계없이 모델의 실행시간을 강하게 예측함
• 모델의 activation을 실행시간에 대한 proxy로 사용
  • 단일 모델 scaling에서 실행시간과 activation 사이의 Pearson 상관은 $r \geq 0.99$
  • 실행시간과 FLOP / parameter 간의 상관관계는 각각 $r = 0.81, r = 0.56$
  • Activation이 heterogeneous 모델에서 실행시간을 완벽하게 예측하지는 못함
    - 서로 다른 실행시간이 걸리는 작업을 사용할 수 있기 때문 (ReLU vs. SiLU)
  • 일부 대형 모델은 activation에서 예측한 것보다 실행시간이 더 높음
    - 해당 모델은 FLOP bound라고 볼 수 있음

모델 실행시간 비교

4. Fast Compound Model Scaling

• Activation과 실행시간은 높은 상관관계를 가지고 있으므로 activation을 최소화하는 scaling 방법이 필요
  • Channel width와 group width를 조절할 때 activation의 증가가 가장 적음
    - 실제로 wide network는 매우 효율적인 모델 중 하나임
    - 하지만 더 deep 하거나 high-resolution 모델에 비해서는 accuracy가 낮을 수 있음
• Fast Comound Model Scaling
  • 모델의 width를 늘리는 대신, depth와 resolution은 상대적으로 덜 확장하는 scaling 전략
  • $\alpha$로 parameterize 되는 scaling 전략으로 공식화
    1. 주어진 $\alpha$에 대해,
       : $e_{d} = \frac{1-\alpha}{2}, e_{w} = \alpha, e_{r} =  \frac{1-\alpha}{2}$
    2. Network를 factor $s$로 scaling 하면,
       : $d' = s^{e_{d}}d, w' = \sqrt{s}^{e_{w}}w, r' = \sqrt{s}^{e_{r}}r$
    3. Group convolution을 사용하는 경우 $g' = \sqrt{s}^{e_{w}}$로 설정
    4. Scale 된 모델의 복잡도
       : $f = sdw^{2}r^{2}, p = s^{\frac{1+\alpha}{2}}dw^{2}, a = s^{\frac{2-\alpha}{2}}dwr^{2}$
  • $\alpha = 1$로 설정하면 width ($w$)에 대한 scaling (가장 작은 activation)
  • $\alpha = 0$으로 설정하면 depth와 resolution ($dr$)에 대한 scaling (가장 큰 activation)
  • $\alpha = \frac{1}{3}$으로 설정하면 depth, width, resolution ($dwr$)에 대한 uniform compound scaling
  • $\frac{1}{3} < \alpha < 1$의 범위에서, $\alpha$가 1에 가까운 scaling 방식이 Fast Compound Scaling
    - $\alpha = 0.8$로 사용
    - $dWr$로 표시

Fast Compound Scaling의 복잡도

5. Experiments

- Settings

• Dataset : ImageNet
• Comparisons : EfficientNet, RegNetY, RegNetZ

EfficientNet baselines

RegNet baselines

- Simple and Compound Scaling

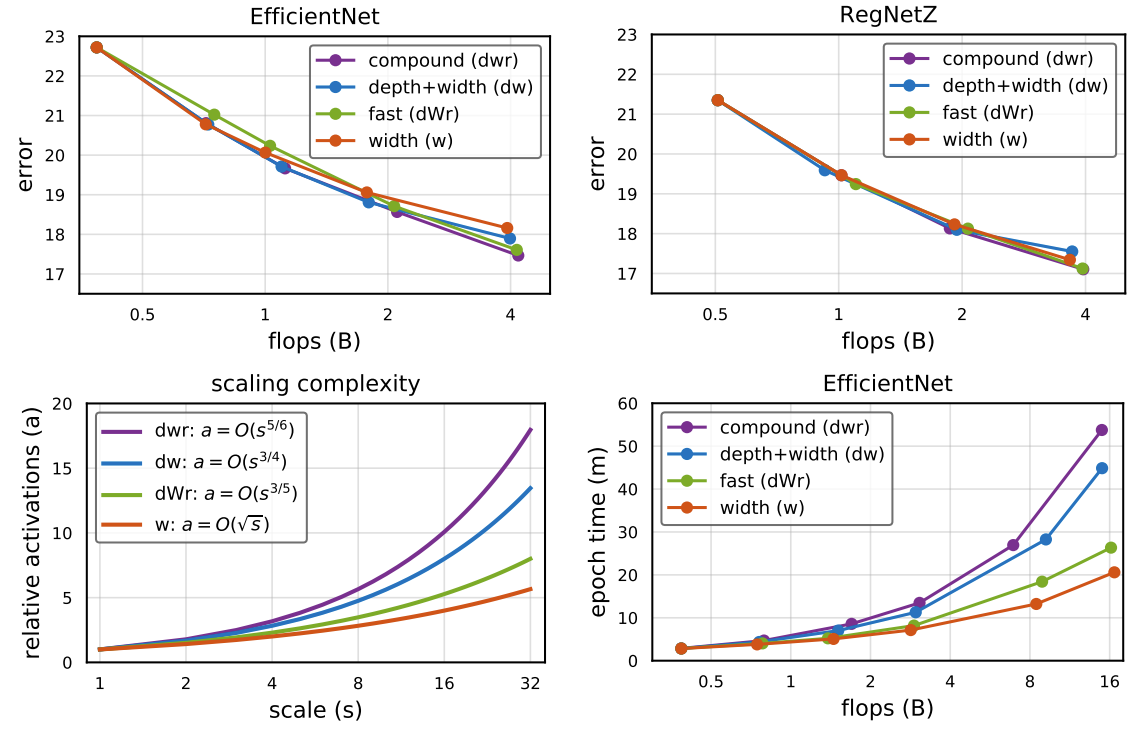
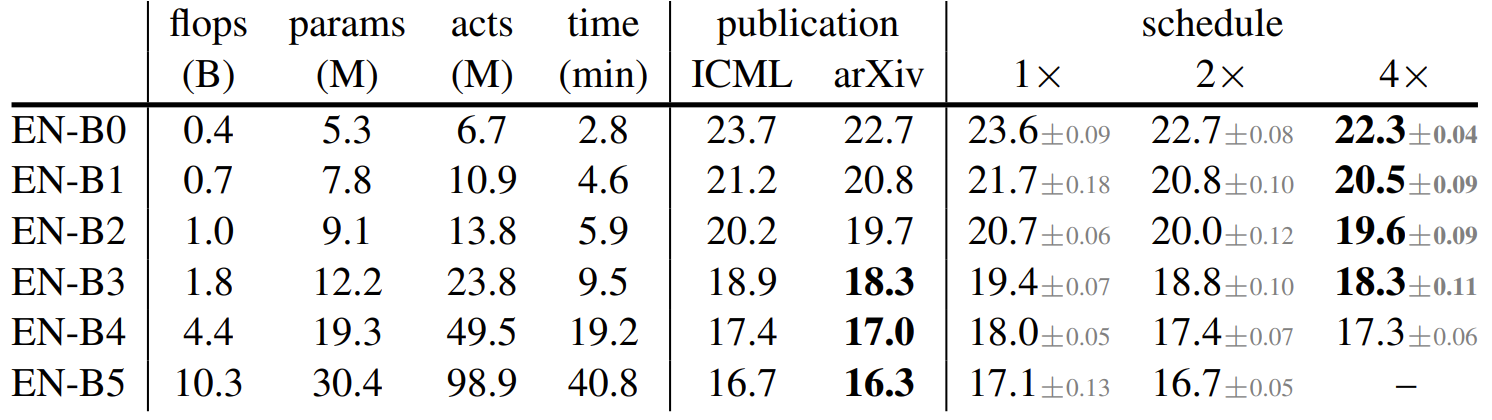
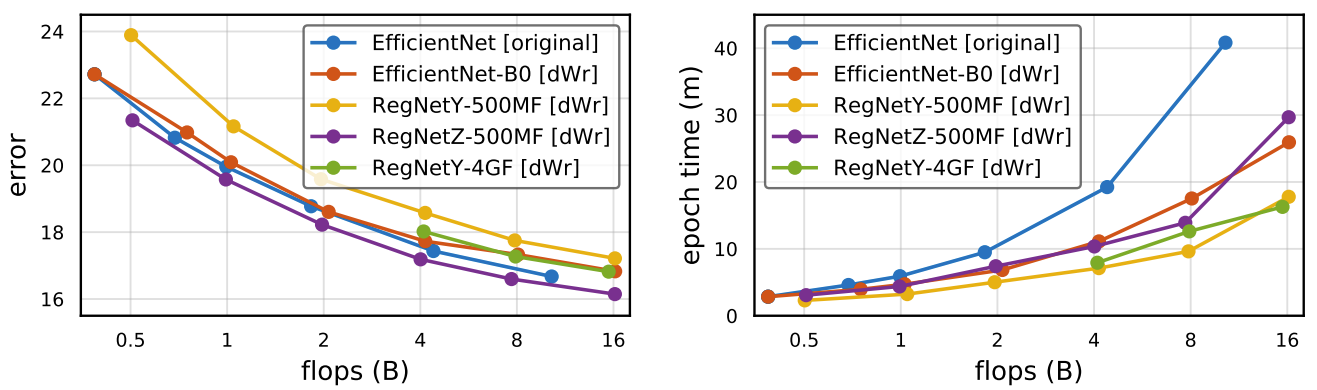
• Width ($w$), Depth ($d$), Resolution ($r)$에 따른 simple scaling, uniform compound scaling ($dwr$)을 통해 scaling 된 EfficientNet-B0의 accuracy와 실행시간을 비교
  • $dwr$ scaling은 최고의 accuracy를 달성하지만 $w$ scaling 보다 느림
  • 차원 pair에 따라 uniform scaling을 시도했을 때도 $dwr$ scaling이 가장 좋은 성능을 보임
• Original compound scaling ($orig$)와 uniform compound sclaing ($dwr$)을 비교
  • $dwr$ scaling은 개별 factor를 최적화할 필요 없이 $orig$와 비슷한 성능을 보임

EfficientNet에서 Compound Scaling 비교

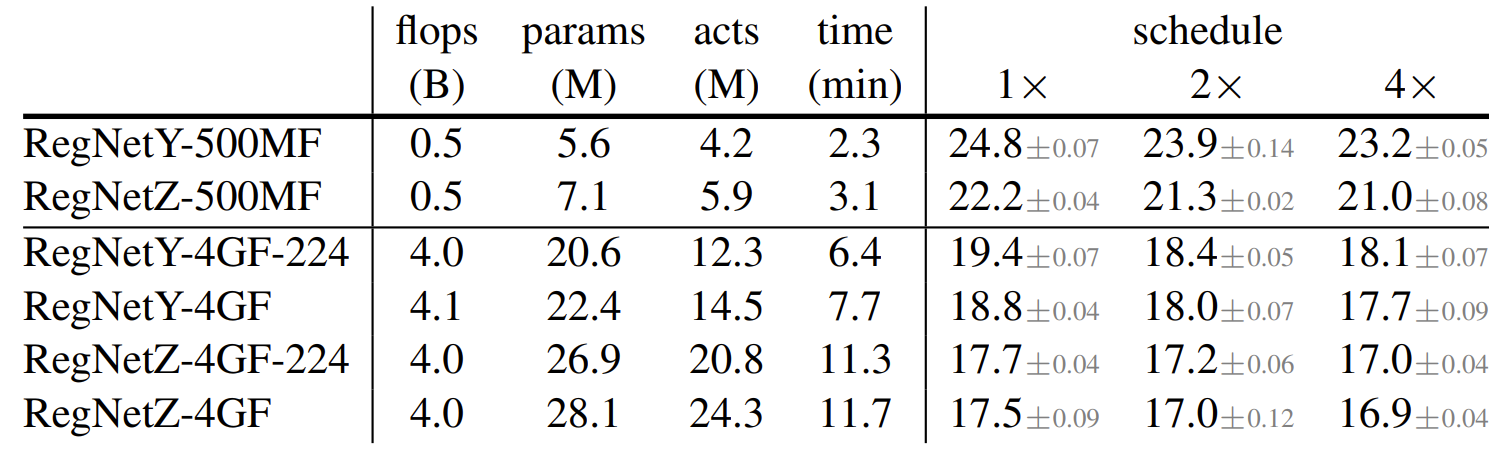
• RegNetY-500MF와 RegNetZ-500MF에 대해 $dwr$ scaling이 가장 좋은 성능을 보임
  - Group width $g$는 width $w$에 비례하여 scaling 됨

RegNet에서 Compound Scaling 비교

- Fast Scaling

• $\alpha = \frac{1}{3}$인 uniform compound scaling ($dwr$)과 $\alpha = 1$일 때 width ($w$) scaling을 interpolate 하는 Fast Compound Scaling 전략 ($dWr$) 비교
  • $\alpha$ 가 1에 가까워질 때 activation이 가장 적게 증가하므로 모델은 더 빨라짐
  • $\alpha = \frac{4}{5}$일 때를 Fast Compound Scaling ($dWr$)로 정의
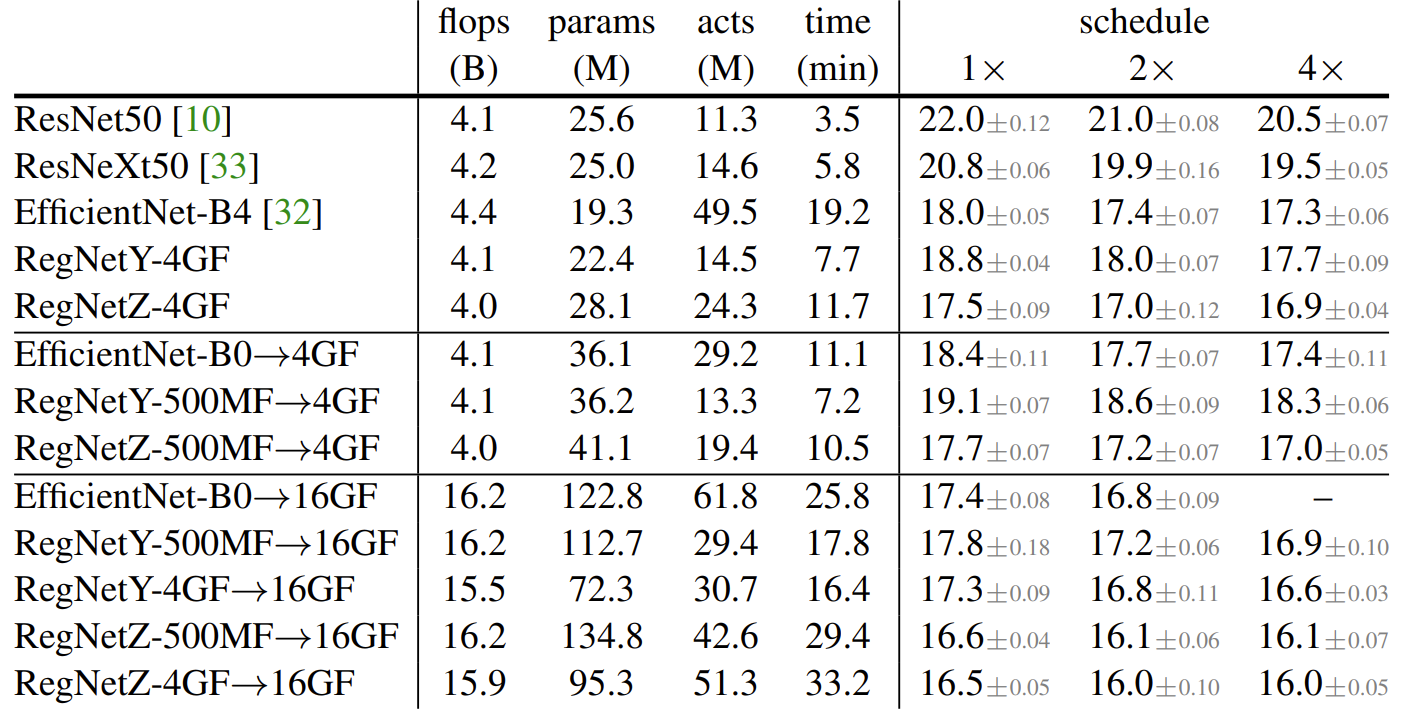
• EfficientNet-B0에서 비교
  • $\alpha < 1$인 경우에 대해 accuracy는 $w$ scaling일 때 보다 더 정확한 성능을 보임
  • 실행속도 측면에서 $dWr$ scaling은 $w$ scaling의 속도와 비슷하고 $dwr$ scaling보다는 훨씬 빠름

EfficientNet에서 Fast Compound Scaling 비교

• RegNet에서 비교
  • 마찬가지로 $dWr$ scaling이 가장 높은 accuracy와 빠른 실행 시간을 달성

RegNet에서 Fast Compound Scaling 비교

- Scaling versus Search

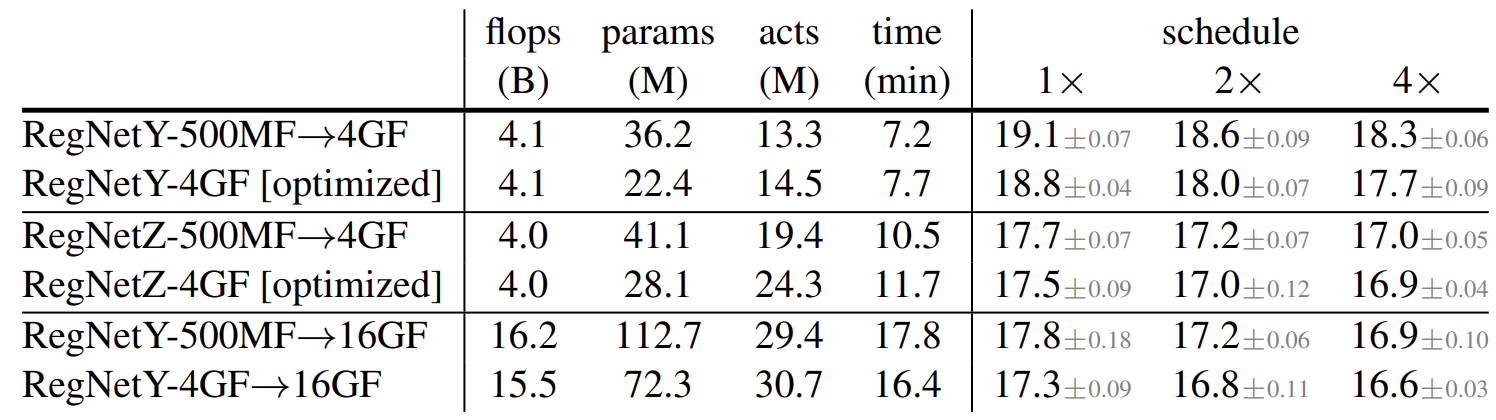
• $dWr$ scaling 한 모델 (RegNetY-500MF $\rightarrow$ 4GF)과 search를 통해 얻은 RegNetY 4GF를 비교
  • Search를 통해 얻어진 모델이 0.6% 정도로 근소한 차이로 우수한 것으로 나타남
    - 높은 accuracy의 모델을 scaling해도 항상 최적의 성능을 가지는 모델을 만들어내는 것은 아님
  • 더 큰 모델로 scaling 하기 전에 intermediate FLOP regime에서 모델을 최적화하는 hybrid 방식의 사용
    - Hybrid 전략으로 얻어진 모델은 0.3% 더 우수한 성능을 보임

Scaling과 Search 비교

- Comparison of Large Models

• 모델 scaling의 장점은 최적화가 불가능한 더 큰 모델로 확장할 수 있다는 것임
• Fast compound scaling을 활용하여 최대 16GF까지 모델을 확장하여 비교
  1. Scale 된 RegNetZ가 가장 높은 accuracy를 달성
  2. Fast compound scaling ($dWr$)을 통해 얻어진 모든 모델은 기존의 EfficientNet 보다 빠름 
  3. 가장 높은 오류를 보인 모델과 가장 낮은 오류를 보인 모델 (RegNetY, RegNetZ)의 차이는 500MF에서 2.2%, 16GF에서 0.8%로 감소함
  4. Intermediate FLOP regime model을 더 높은 FLOP 모델로 확장하는 hybrid 방식은 RegNetY와 RegNetZ의 격차를 해소할 수 있음
  5. RegNetY는 가장 빠른 속도를 가진 모델이고, 높은 FLOP에서 실행시간이 제한되는 경우 좋은 선택일 수 있음

대형 모델에서 Fast Compound Scaling 비교

• RegNetY-4GF $\rightarrow$ 16GF는 EfficientNet-B4 보다 4배 더 많은 FLOP을 사용함에도 불구하고 더 적은 메모리와 더 빠른 속도를 보임

대형 모델로의 scaling 결과 비교