[Paper 리뷰] beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework

beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework

---

• Supervision 없이 독립적인 data의 interpretable factorised representation을 학습하는 것이 중요
• $\beta$-VAE (beta-VAE)
  • Unsupervised 방식으로 raw image data에서 interpretable factorised latent representation을 발견 가능
  • adjustable parameter $\beta$ : latent channel capacity와 재구성 정확도의 independence 제약조건 조절
• $\beta$-VAE는 train이 stable하고, data에 대한 가정이 적고, 하나의 hyperparameter $\beta$ 튜닝만 신경 씀

• 논문 (ICRL 2017) : Paper Link

---

1. Introduction

• data representation 선택에 따라서 학습의 난이도는 크게 달라지고 모델 향상도 가능
  • disentangled representation을 학습해서 사용하는 것은 매우 유용
    - disentangled representation은 single latent unit이 다른 factor의 변화에는 무관하지만 single generative factor에는 민감한 것으로 정의됨
    - For example, 3D object에서 object identity, position, scale, lighting, color 등의 요소
  • generative factor에 대한 disentangled posterior distribution의 unsupervised learning은 주요한 관심사
    - data generative factor의 특성/갯수에 대한 사전 지식이 필요
• disentangled factor learning을 위해 scalable unsupervised 방법인 InfoGAN이 등장
  • However, 
    - InfoGAN은 학습이 불안정하고 sample diversity가 감소하는 문제가 존재
    - InfoGAN은 사전 분포 선택과 정규화 노이즈 변수에 민감하기 때문에 data 사전 지식을 많이 요구
    - transfer learning, zero-shot 추론시 unsupervised model의 posterior latent distribution을 사용하는 것도 중요
  • InfoGAN보다 unsupervised learning에 적합한 방식이 필요
• 학습된 disentanglement를 정량화하는 방식이 없음
  • disentanglement 정도를 비교하기 위한 방법도 필요

-> 그래서 $\beta$-VAE 제안

< Overall of $\beta$-VAE >

1. $\beta$-VAE
   • 독립적인 visual data의 generative factor에 대한 disentangled representation을 학습하기 위한 unsupervised approach
   • unsupervised data에서 독립적인 latent factor를 학습하는 disentangled factor learning을 사용
   • hyperparameter $\beta$
     • 기존 VAE에 학습 제약조건을 조절하는 parameter를 추가
     • 제약조건은 latent information channel의 capacity에 제한을 주고, 독립적인 latent factor 강조를 제어
     • $\beta$가 1이면 기존 VAE와 동일
2. 서로 다른 모델의 학습된 disentanglement에 대한 정량적 척도 제시
3. 기존 모델들과 비교해서 $\beta$-VAE의 State-of-the-art 성능 달성

2. $\beta$-VAE Framework Derivation

• 입력 data 집합 $D=\{X, V, W\}$ 
  • $X$ : 이미지, $V$ : 조건부 독립 factors, $W$ : 조건부 종속 factors
  • $V$와 $W$는 ground truth data generative factors
  • (가정) $p(x|v,w) = Sim(v,w)$ : 이미지 $X$는 연관된 ground truth data generative factors를 사용하여 시뮬레이터 $Sim()$을 통해 생성
    
    
• $\beta$-VAE의 목표
  • $X$의 샘플만 사용해서 관측된 data $x$의 joint distribution과 generative latent factor $z$를 학습하여 $z$로 부터 관측된 데이터 $x$를 생성하는 것 
  • latent factor $z$의 전체 분포의 기대값에서 관측된 data $x$에 대한 marginal log-likelihood를 최대화 

$\beta$-VAE Objective Formulation

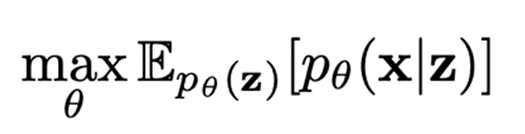
Step 1. 주어진 observation $x$에 대한 latent factor $z$의 추정된 사후 분포 $q_{\phi}(z|x)$

• 추정된 latent factor $q_{\phi}(z|x)$가 generative factor $v$의 disentangled를 학습해야 함
• 조건부 종속 generative factor $w$는 $v$를 표현하는데 사용되지 않고 남아있는 $z$의 부분집합에 entangled 상태로 남아있음
• $q_{\phi}(z|x)$에서 disentangling property를 활용하기 위해서 제약조건을 도입
  • latent information bottleneck capacity를 제어하고 통계적 독립을 만족할 수 있는 사전 $p(z)$와의 일치 조건
  • $p(z) = N(0,I)$ : 사전 분포를 isotropic unit Gaussian dist.으로 두고 제약된 최적화 문제를 고려
  • $\epsilon$ : 적용된 제약조건의 강도

Step 1으로 유도되는 식

Step 2. Largrangian 기반 식 재구성

• KKT 조건 하에서 Largrangian 적용

Step 2로 유도되는 식

Step 3. $\beta$ coefficient

• KKT multiplier $\beta$
  • regularization coefficient의 역할
    - latent information channel $z$의 capacity를 제한
    - isotropic Gaussian dist. $p(z)$로 학습된 사후 분포에 독립적인 압력
  • KKT 조건의 complementary slackness에 따라서 $\epsilon\geq0$이므로 $\beta$ coefficient 추가

Step 3로 유도되는 식

Step 4. 다양한 $\beta$ 값 대응

• 다양한 $\beta$ 값은 training 중에 적용되는 learning pressure를 변경하므로 다양한 학습 표현을 얻게 함
  • $\beta=1$인 경우 : 일반적인 VAE와 동일
  • $\beta\gt1$인 경우 : 기존 VAE 보다 강한 제약, 조건부 독립인 generative factor $v$의 disentangled representation 학습 가능
• 제약 조건은 training data $x$의 log-likelihood를 최대화 하는 것과 결합하여 모델이 data의 가장 효과적인 표현을 학습하도록 $z$의 capacity를 제한
  • data $x$는 조건부 독립 ground truth factor $v$를 통해 생성되고 $D_{KL}$ 항은 $q_{\phi}(z|x)$에서 조건부 독립성을 지원
  • $v$의 disentangled representation을 학습하기 위해서는 더 큰 $\beta$ 값이 필요
  • 큰 $\beta$ 값은 학습된 latent representation에서 reconstruction과 disentanglement의 trade-off를 만듦
    - disentangled representation은 latent channel capacity restriction과 information preservation 사이의 균형을 만족하면 나타남
    - latent channel capacity restriction은 latent bottleneck을 통과할 때 high frequency detail의 손실이 발생해 재구성을 불완전하게 함
    -> 학습된 모델에서 data의 log-likelihood는 $\beta$-VAE의 disentangling을 평가하기에는 좋지 않은 metric

-> 그래서 새로운 disentanglement metric을 추가

 

3. Disentanglement Metric

Disentanglement Metric

Step 1. disentangled representation이 가질 수 있는 속성 정의

• (가정) data는 독립적이고 해석가능한 generative factor를 사용하는 시뮬레이터로부터 생성 ($\beta$-VAE derivation 가정과 동일)
  • For example, 물체 모양, 색상, 크기 속성 -> 작은 초록색 사과 생성
  • 독립된 속성으로 인해 빨간 사과, 초록색 사과 생성이 가능
• separate latent로 인코딩한 generative factor로부터 얻어지는 disentangled representation
  • 단순한 linear classifier로도 분류 가능
  • 독립된 latent representation이 disentangled일 필요는 없기 때문에 PCA를 적용하는 것도 가능
    - 이런 방식으로 학습한 표현은 일반적으로 generative factor와 일치하지 않으므로 interpretability가 떨어짐
    - cross-correlation은 disentangled metric으로 적합하지 않음

Step 2. Disentangled Metric 정의

• 추론된 latent의 독립성과 interpretability를 모두 측정하는 metric을 제안
  • 하나의 data generative factor를 고정하고 다른 것들은 random sampling 하여 생성된 이미지를 추론
  • 독립성, interpretability가 추론된 latent에서 유지되는 경우 고정된 generative factor와 연관된 latent와의 분산이 작음
  • low capacity linear classifier를 사용해 얻은 accuracy value를 disentanglement metric score로 사용
  • target factor와 연관된 latent의 분산이 작을 수록 제안된 metric의 값은 커짐
• Disentanglement Metric Score
  
  1. vector $z^{b}_{diff}$를 가지는 batch $B$ 구성
  2. factor $y \sim Unif[1...K]$인 $y$ 선택
  3. for $L$ sample의 Batch 마다 :
     - 두개의 latent representation $v_{1, l}$, $v_{2, l}$ sampling
     - 이미지 $x_{1, l} \sim Sim(v_{1, l})$를 생성한 다음, encoder $q(z|x)$를 사용해서 latent factor $z_{1, l}$ 추론
     - $v_{2, l}$도 동일과정 적용
  4. 추론된 latent represnetation의 절대값 차이 $z^{l}_{diff} = |z_{1,l}-z_{2,l}|$ 계산
  5. $z^{l}_{diff}$의 평균 $z^{b}_{diff} = {1 \over L} \Sigma^{L}_{l=1}z^{l}_{diff}$을 사용해서 $p(y|z^{b}_{diff})$를 예측
  6. 이 predictor의 정확도를 disentanglement metric score로 사용
• predictor의 목표는 주어진 $z^{b}_{diff}$에 대해서 고정된 generative factor $y$를 예측하는 것
  • nonlinear disentangling 능력을 없애기 위해서 단순 linear classifier를 사용

4. Experiments

- Settings

• dataset : celebA, chairs, faces
• comparisons : VAE, InfoGAN, DC-IGN

- Qualitative Benchmarks 

• $\beta$-VAE는 supervision 없이 수행 가능하므로 unlabelled data의 generative factor를 학습
  • (chair data) DC-IGN과 달리 design, chair width, leg style 학습 
  • $\beta$-VAE만이 3개의 factor를 발견

chair data

• $\beta$-VAE의 disentangled factor 비교
  • (celebA data) $\beta$-VAE와 InfoGAN 만이 disentangled factor를 학습
  • $\beta$-VAE는 더 많은 disentangled factor를 찾음 (skin color, image saturation, age/gender)
  • $\beta$-VAE는 더 정확하게 disentangled factor를 구분 (sunglasses의 존재)
  • VAE는 entangled representation을 학습 (emotion, glass, gender가 같이 바뀜)

Learnt latent factors of celebA data

celebA data

• $\beta$-VAE의 latent는 InfoGAN보다 smooth contimuous transformation을 학습
  • (3D faces) azimuth angles에 대한 연속적인 interpolate
  • $\beta$-VAE는 넓은 범위의 azimuth angle을 학습

3D faces data

• $\beta$-VAE는 robust하게 더 많은 latent factor를 발견하고 깔끔하게 disentangled representation을 학습
  • data에 대한 불필요한 가정이 없기 때문에 train이 안정적이기 때문
• VAE와 비교했을 때 $\beta$ 조절에 따라서 disentangled latent representation 품질이 달라짐
  • $\beta$를 늘리면 더 좋은 disentangledment를 얻을 수 있음
  • 대신 흐릿한 reconstruction과 일부 factor에 대한 representation 손실이 생김

- Quantitative Benchmarks

• 제안한 disentanglement metric 사용하고, 모델들의 representation을 비교
  • $\beta$-VAE는 unsupervised 방법임에도 불구하고, semi-supervised인 DC-IGN과 비슷한 성능을 보임
  • $\beta$가 작은 경우 reconstruction이 entangled representation과 많이 연관되어 있음
  • $\beta$가 큰 경우 높은 disentangled score를 가지고, 흐릿한 reconstruction과 연관되어 있음

Disentanglement metric & representation 비교

- Understanding the effect of $\beta$

• $\beta$ coefficient를 활용해 독립적인 generative factor로 부터 disentangled representation을 학습하는 제한된 최적화를 고려
• 좋은 disentanglement를 얻기 위해서는 $\beta \gt 1$이 요구됨
  • $\beta$가 너무 작거나 너무 큰 경우 모델은 entangled latent representation을 학습
    - latent $z$ bottleneck의 capacity가 너무 작거나 크게 구성되기 때문
  • 좋은 disentangled representation은 흐릿한 reconstruction으로 이어짐
    - latent $z$의 capacity가 제한되기 때문
    - entangled representation은 깔끔한 reconstruction이 가능
  • 적절한 $\beta$ 값을 찾는 것은 좋은 결과를 얻을 수 있지만, 완벽한 reconstruction에 투자할 필요는 없음
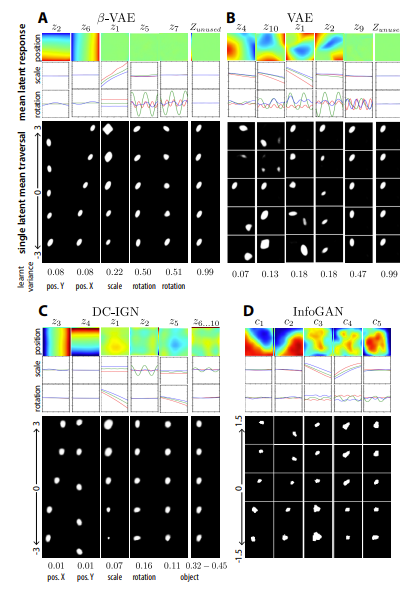
• $\beta$-VAE, DC-IGN만 PostX, PostY, Scale, Roatation에 대한 disentanglement를 잘 얻었음

Representations learnt by $\beta$-VAE ($\beta=4$)