[Paper 리뷰] MSMC-TTS: Multi-Stage Multi-Codebook VQ-VAE based Neural TTS

MSMC-TTS: Multi-Stage Multi-Codebook VQ-VAE based Neural TTS

---

• Vector-quantized, compact speech representation을 도입하여 neural text-to-speech의 성능을 향상할 수 있음
• MSMC-TTS
  • Vector-Quantized Variational AutoEncoder based feature를 채택하여 acoustic feature를 서로 다른 time resolution의 sequence로 encoding 하고, 이를 multiple codebook으로 quantize 함
  • Prediction 과정에서는 multi-stage predictor는 Euclidean distance와 triplet loss를 최소화하여 input text sequence를 Multi-Stage Multi-Codebook Representation에 stage-wise로 mapping 함
• 논문 (TASLP 2023) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS)는 text를 해당하는 speech audio로 변환하는 것을 목표로 하고, 특히 neural network를 활용하는 neural TTS는 high-fidelity의 성능을 보이고 있음
  • 일반적으로 neural TTS framework는 아래 그림과 같이 analysis, prediction, synthesis로 구성됨
    1. Analysis에서 raw waveform은 signal processing을 통해 pitch, line spectrum, mel-cepstra 등의 acoustic feature sequence로 compress 됨
       - Waveform과 비교하여 해당 feature는 더 짧은 sequence length와 더 적은 parameter로 speech를 나타낼 수 있으므로 text에서 더 쉬운 prediction이 가능함
    2. 이후 해당 feature로부터 waveform을 reconstruct 하기 위해 nerual vocoder를 적용함
       - 대표적으로 WaveGlow, MelGAN 등을 사용할 수 있고, 이를 통해 acoustic model로부터 예측된 acoustic feature를 처리하여 TTS를 수행할 수 있음
  • BUT, 예측된 acoustic feature로부터 합성된 audio는 ground-truth acoustic feature로 합성된 audio와 동일한 수준의 fidelity를 달성할 수 없음
    - Acoustic model의 prediction error로 인해 예측된 feature는 낮은 품질을 가지기 때문
    
  • 특히, prediction error는 ground-truth의 distribution과 차이를 만들기 때문에, ground-truth feature 만으로 training 된 vocoder에서 out-of-domain data에 대한 generalization 문제를 일으킴
    
    1. 한편으로 해당 문제를 해결하기 위해 기존에는 다음의 방법들이 도입됨
       - Self-attention based model을 도입하여 sequential modeling 성능을 향상하는 방법
       - Generative Adversarial Network (GAN), Flow-based 등의 generative model을 활용하는 방법
       - Target waveform과 예측된 acoustic feature를 align 하고 fine-tuned vocoder를 사용하는 방법
       - Acoustic feature를 사용하지 않고 text representation을 waveform에 직접 mapping 하는 end-to-end 방법
    2. BUT, 이러한 기존의 model-oriented approach들은 modeling complexity가 높고 training/inference를 위한 많은 computing resource가 필요함
       - 따라서, speech feature representation 측면에서 해당 문제들을 접근하는 것이 필요함

• 일반적으로 speech representation은 richer information을 반영하기 위해 higher dimension이나 larger space volume으로 할당되지만, overly large space는 input/output으로 사용될 때 overfit 또는 underfit 될 수 있음
  • 즉, large representation은 acoustic model의 prediction error를 증가시키고 vocoder의 generalization을 약화시킴
  • 따라서 고품질 TTS를 보장하기 위해 좋은 speech representation은 다음을 고려해야 함:
    
    1. Completeness : target speech는 speech representation으로부터 well-reconstruct 될 수 있어야 함 (self-consistency)
    2. Compactness : target speech는 적은 parameter와 small space volume으로 represent 될 수 있어야 함
       - 즉, speech representation은 high completness를 통해 high-fidelity의 reconstruction을 달성하면서 효과적인 prediction을 위한 high compactness를 보장해야 함
  • 이때 representation learning에서 주로 활용되는 autoencoder는 encoder-decoder architecture를 기반으로 target data의 latent representation을 학습할 수 있음
    - 여기서 input feature는 encoder에 의해 latent representation으로 변환되고, decoder에 의해 reconstruct 됨
    - 즉, reconstruction 품질이 좋을수록 representation의 completness가 높아짐
  • 한편으로 latent representation의 sparsity와 compactness를 control 하기 위해 다양한 constraint를 적용할 수 있음
    - 특히 vector-quantized variational autoencoder (VQ-VAE)를 통한 discrete latent representation은 뛰어난 compactness를 보임

Neural TTS Framework

-> 그래서 completeness, compactness를 모두 만족하는 speech representation을 얻기 위해 VQ-VAE를 채택한 MSMC-TTS를 제안

 

• MSMC-TTS
  • 먼저 neural vocoder에서 일반적으로 사용되면서 충분한 completeness를 가지는 mel-spectrogram을 기반으로 compact speech representation을 construct 하는 feature analyzer를 training
  • 이후, 해당 high-compactness representation의 completeness를 보완하기 위해 Multi-Stage Multi-Codebook (MSMC) approach를 도입
    - 이때 multi-codebook은 richer representation을 얻기 위해 vector를 quantize 하고, 서로 다른 time resolution에서 speech information을 equally preserve 하기 위해 speech sequence를 multiple sub-sequence로 quantize 함
  • 결과적으로 MSMC-TTS는 위 과정을 통해 얻어지는 Multi-Stage Multi-Codebook Representation (MSMCR)을 통해 text로부터 speech audio를 생성
    1. 여기서 MSMCR은 feature analyzer로 추출되고, nerual vocoder에 의해 audio로 reconstruct 됨
    2. 추가적으로 multi-stage predictor는 input text의 resolution에서 MSMCR을 예측하는 acoustic model로써, MSE와 triplet loss를 결합한 loss function으로 training 됨

< Overall of MSMC-TTS >

• Completeness, compactness를 만족하는 speech representation을 얻기 위해 VQ-VAE 기반의 MSMC approach를 도입하고, 해당 MSMCR을 활용하여 reconstruction을 수행
• 결과적으로 기존보다 고품질의 TTS 성능을 달성

2. Vector Quantization-based Compact Speech Representation

- Vector Quantized Variational AutoEncoder

• VQ-VAE는 encoder-decoder architecture를 기반으로 target data로부터 discrete latent representation을 학습하는 것을 목표로 함
  • 아래 그림과 같이 VQ-VAE는 encoder, decoder, VQ operation으로 구성됨
    1. 먼저, input speech sequence $\mathbf{x}=\{x_{1},x_{2},...,x_{L}\}$은 encoder $\mathbf{E}$를 통해 encoding됨:
       (Eq. 1) $\tilde{\mathbf{z}}=\mathbf{E}(\mathbf{x})$
    2. 그러면 vector-quantized latent representation $\mathbf{z}$는:
       (Eq. 2) $\mathbf{z}=Q(\tilde{\mathbf{z}};\mathbf{c})$
       - $\mathbf{c}$ : $N$ dimension을 가지는 $M$개의 codeword를 포함하는 codebook
    3. 각 latent vector $\tilde{z}_{i}$에 대해 quantizer $Q$는 representation을 모든 codeword와 compare 하고, Euclidean distance에 따라 가장 가까운 것을 quantized output $z_{i}$로 선택함:
       (Eq. 3) $z_{i}=c_{j^{*}} \,\, \mathrm{where}\,\, j^{*}=\arg\min_{1\leq j \leq M}|| \tilde{z}_{i}-c_{j}||_{2}^{2}$
       
    4. 최종적으로, output speech sequence $\hat{\mathbf{x}}$는 decoder $\mathbf{D}$를 통해 reconstruct 됨:
       (Eq. 4) $\hat{\mathbf{x}}=\mathbf{D}(\mathbf{z})$
  • Training 시 VQ-VAE는 $\mathbf{x}, \hat{\mathbf{x}}$ 간의 Euclidean distance를 최소화하여 speech reconstruction을 학습함
    - BUT, non-differentiable VQ operation으로 인해 decoder의 gradient는 encoder로 backpropagate 되지 않음
  • 따라서 논문은 encoder training을 위해, $\mathbf{z}, \tilde{\mathbf{z}}$ 사이의 Euclidean distance를 최소화하는 additional loss term을 도입하고, 이때 complete loss function은:
    (Eq. 5) $\mathcal{L}_{vqvae}=\mathcal{D}_{e}(\hat{\mathbf{x}},\mathbf{x})+\alpha\mathcal{D}_{e}(\tilde{\mathbf{z}},\text{sg}(\mathbf{z})) = \frac{1}{L}\sum_{i=1}^{L}|| \hat{x}_{i}-x_{i}||_{2}^{2}+\frac{\alpha}{L}\sum_{i=1}^{L}|| \tilde{z}_{i}-\text{sg}(z_{i})||_{2}^{2}$
    - $\mathcal{D}_{e}(*,*)$ : Euclidean distance, $\text{sg}(*)$ : stop-gradient operation, $\alpha$ : coefficient
  • Codebook 내의 codeword는 exponential moving average를 사용해 update 됨:
    (Eq. 6) $\hat{u}_{j}^{(t)}=\beta\hat{u}_{j}^{(t-1)}+(1-\beta)u_{j}, \,\, \hat{v}_{j}^{(t)}=\beta\hat{v}_{j}^{(t-1)}+(1-\beta)v_{j}, \,\, c_{j}=\frac{\hat{v}_{j}^{(t)}}{\hat{u}_{j}^{(t)}}$
    - $u_{j}, v_{j}$ : 각각 $t$-th training iteration에서 mini-batch $c_{j}$로 quantize 된 hidden vector $\{\tilde{z}_{i}\}$의 수와 합
    - $\beta$ : 0~1 사이의 coefficient로 논문에서는 0.99로 설정

VQ-VAE Framework

- Compactness of Vector-Quantized Representation

• Acoustic feature sequence는 index sequence로 represent 될 수 있음
  • $N$개의 number로 구성된 vector (number 당 $B$ bits)를 $1$에서 $M$ range를 가지는 하나의 integer로 compress 할 때의 compression rate $\mathcal{R}$은:
    (Eq. 7) $\mathcal{R}=\frac{N*B}{\log_{2}(M)}$
    - 이를 통해, 80-dim Mel-spectrogram (32-bit float-point number)을 $2560/\log_{2}(M)$배로 compress 할 수 있음
  • Compression ratio가 높을수록 feature compactness는 높아지지만, information loss도 증가하므로 feature completeness는 낮아짐
    - 따라서 고품질 reconstruction을 위해, 논문은 해당 VQ-representation (VQR)을 더욱 최적화할 수 있는 multi-stage multi-codebook approach를 도입함

3. Multi-Stage Multi-Codebook VQ-VAE

• MSMC-VQ-VAE based feature analyzer는 speech sequence를 Multi-Stage Multi-Codebook Representation (MSMCR)로 stage-wise로 encode 하는 것을 목표로 함
  • 즉, 서로 다른 time resolution의 sub-sequence set은 multiple codebook에 의해 각각 quantize 됨
  • 이를 위해 논문은 multi-head vector quantization과 multi-stage autoencoder를 활용

- Multi-Head Vector Quantization

• VQR에서 compression rate를 줄이면 richer representation을 얻을 수 있지만, 이를 VQ-VAE에서 계산하기는 어려움
  • 예시로, compression ratio를 절반으로 줄이기 위해서는 (Eq. 7)의 $\log_{2}(*)$ 연산으로 인해 codebook size는 제곱으로 커져야 함
    - 즉, 각 codeword를 training 하기 위한 computational requirement는 exponential 하게 증가함
  • 따라서 논문은 quantization 계산을 위해 Multi-Head Attention Mechanism을 응용한 Multi-Head Vector Quantization (MHVQ)을 도입함
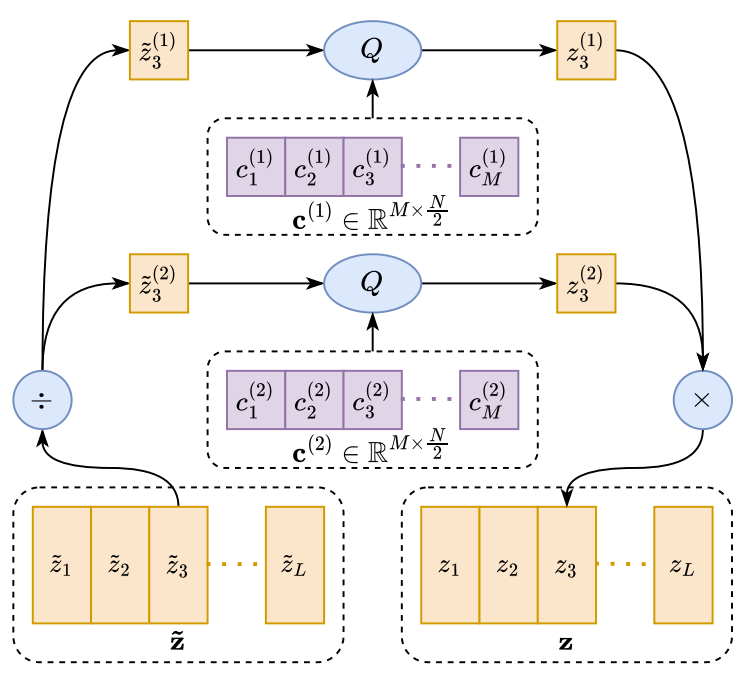
    1. 먼저 아래 그림처럼 MHVQ에서 하나의 VQ codebook $\mathbf{c}\in \mathbb{R}^{M\times N}$은 $H$개의 sub-codebook $\left\{ \mathbf{c}^{(i)}\in\mathbb{R}^{M\times \frac{N}{H}},\,\, \mathrm{for}\,\, i=1,2,..,H\right\}$으로 evenly chunk 됨
       
    2. 이때 input vector $x\in\mathbb{R}^{N}$은 다음과 같이 quantize 됨:
       (Eq. 8) $x^{(1)},...,x^{(H)}=\mathrm{Chunk}(x,H)$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, y^{(i)}=Q(x^{(i)};\mathbf{c}^{(i)})\,\, \mathrm{for}\,\, i=1,...,H$
       $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, y=\mathrm{Concat}(y^{(1)},...,y^{(H)})$
       - $x$는 $\frac{N}{H}$ dimensionality를 가지는 $H$개의 sub-vector로 chunck 된 후, 해당하는 codebook으로 quantize 됨
       - 이후 quantized sub-vector는 output vector $y$와 concatenate 됨
    3. 여기서 compression ratio는:
       (Eq. 9) $\mathcal{R}=\frac{1}{H}*\frac{N*B}{\log_{2}(M)}$
       
  • 위 방식을 통해 codebook 수를 doubling 하면서도, $\log_{2}(*)$로 인해 발생하는 requirement를 회피해 compression rate를 효과적으로 줄일 수 있음

Multi-Head Vector Quantization

- Multi-Stage AutoEncoder

• Completeness를 향상하는 것뿐만 아니라, segmental pronunciation과 같은 다양한 time resolution의 speech attribute를 well-represent 하는 것도 중요함
  • 그렇지 않으면 Cannikin Law에 따라 overly compressed attribute는 전체 품질에 심각한 영향을 줄 수 있음
  • 따라서 논문은 다양한 time resolution에서 speech sequence를 모델링하는 multi-stage autoencoder를 도입함
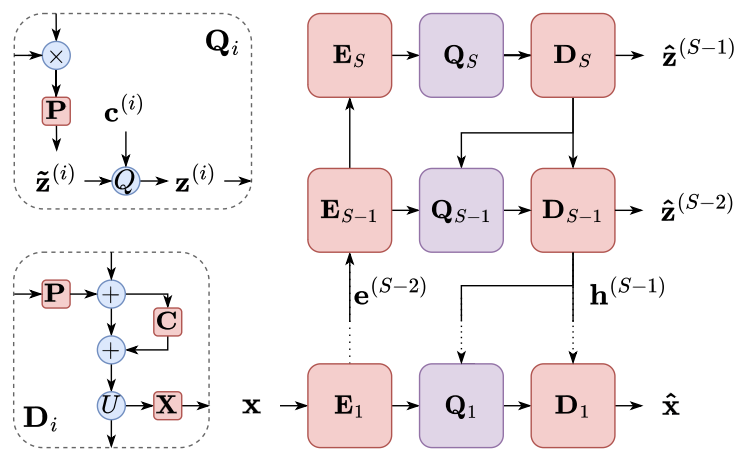
    1. 먼저 multi-stage autoencoder는 codebook group $C=\{\mathbf{c}^{(1)},...,\mathbf{c}^{(S)}\}$를 사용하여 input sequence $\mathbf{x}$를 multi-stage vector-quantized representation $Z=\{\mathbf{z}^{(1)},...,\mathbf{z}^{(S)}\}$로 encoding 함
       - $S$ : stage 수
       - 특히 MHVQ가 적용되는 경우, codebook $\mathbf{c}^{(i)}$는 sub-codebook group $\{\mathbf{c}^{(i,1)},...,\mathbf{c}^{(i,H)}\}$를 나타냄
    2. 이후 encoder는 input speech sequence $\mathbf{x}$를 encoding sequence $\{\mathbf{e}^{(1)},...,\mathbf{e}^{(S)}\}$로 encoding 함:
       (Eq. 10) $\mathbf{e}^{(i)}=\left\{\begin{matrix}
       \mathbf{E}_{i}(\mathbf{x}), & \mathrm{if}\,\, i=1 \\
       \mathbf{E}_{i}(\mathbf{e}^{(i-1)}), & \mathrm{if}\,\,i>1  \\
       \end{matrix}\right.$
    3. 각 encoder block 이전의 strided convolution layer는 sequence를 lower time resolution으로 downsampling 하고, sequence는 highest stage에서부터 단계적으로 quantize 됨:
       (Eq. 11) $\mathbf{z}^{(i)}=\left\{\begin{matrix}
       \mathbf{Q}_{i}(\mathbf{e}^{(i)},\phi,\mathbf{c}^{(i)}), & \mathrm{if}\,\,i=S \\
       \mathbf{Q}_{i}(\mathbf{e}^{(i)},\mathbf{h}^{(i+1)},\mathbf{c}^{(i)}), & \mathrm{if}\,\, i<S \\
       \end{matrix}\right.$
       - $\phi$ : no input, $\mathbf{c}^{(i)}$ : codebook (MVHQ가 적용된 경우, $\mathbf{c}^{(i)}=\{\mathbf{c}^{(i,1)},...,\mathbf{c}^{(i,H)}\}$)
       - 즉, quantizer block $\mathbf{Q}_{i}$에서 $\mathbf{e}^{(i)}$는 higher-stage decoder의 hidden sequence $\mathbf{h}^{(i+1)}$과 concatenate 되고, projection layer에 의해 변환되어 다음 quantization에 대한 $\tilde{\mathbf{z}}^{(i)}$를 얻음
  • Quantized sequence $\mathbf{z}^{(i)}$는 decoder $\mathbf{D}_{i}$에 의해 처리되어 다음 quantization과 decoding을 위한 $\mathbf{h}^{(i)}$를 얻음
    1. 여기서 next-stage quantized sequence $\mathbf{z}^{(i-1)}$이나 speech sequence $\mathbf{x}$를 예측하려면:
       (Eq. 12) $\left\{\begin{matrix}
       \mathbf{h}^{(i)},\hat{\mathbf{z}}^{(i-1)}=\mathbf{D}_{i}(\mathbf{z}^{(i)},\phi), & \mathrm{if}\,\, i=S \\
       \mathbf{h}^{(i)},\hat{\mathbf{z}}^{(i-1)}=\mathbf{D}_{i}(\mathbf{z}^{(i)}, \mathbf{h}^{(i+1)}), & \mathrm{if}\,\, 2\leq i \leq S-1 \\
       \mathbf{x} =\mathbf{D}_{i}(\mathbf{z}^{(i)},\mathbf{h}^{(i+1)}), & \mathrm{if}\,\, i=1  \\
       \end{matrix}\right.$
    2. Decoder $\mathbf{D}_{i}$는 quantized sequence $\mathbf{z}^{(i)}$를 projection을 통해 변환하고, $i<S$일 때 $\mathbf{h}^{(i+1)}$을 추가함
       - Residual convolutional layer는 이를 처리한 다음, $\mathbf{h}^{(i)}$로 repitition 하여 upsampling 함
       - Output sequence는 예측을 위해, 다른 neural network module $\mathbf{X}$에서도 처리됨
  • 결과적으로, loss function은:
    (Eq. 13) $\mathcal{L}_{msmc}=\mathcal{D}_{e}(\mathbf{x},\hat{\mathbf{x}})+\frac{\alpha}{S}\sum_{j=1}^{S}\mathcal{D}_{e}\left(\tilde{\mathbf{z}}^{j},\mathrm{sg}(\mathbf{z}^{(j)})\right)+\frac{\beta}{S-1}\sum_{j=1}^{S-1}\mathcal{D}_{e}\left(\hat{\mathbf{z}}^{(j)},\mathrm{sg}(\mathbf{z}^{(j)})\right)$
    - $\alpha, \beta$ : weight coefficient
    - (Eq. 13)은 $\mathcal{L}_{vqvae}$와 유사하지만, 두 번째 term은 모든 latent sequence에 대해 $\mathcal{D}_{e}$를 계산하고 세 번째 term은 예측된 latent sequence가 target에 가까워지도록 함
  • Multi-stage modeling에서 deep network는 lower-stage module에 대한 overfitting에 취약하므로 higher-stage latent sequence는 meaningless 함
    - 따라서 MSMC-TTS는 high-stage sequence에서 low-stage representation을 예측하도록 training 됨

Multi-Stage, Multi-Codebook VQ-VAE

4. MSMC-TTS

- System Framework

• MSMC-TTS는 아래 그림과 같이, analysis/prediction/synthesis의 3가지 module로 구성됨
  1. 먼저 analysis module에서 speech signal $\mathbf{s}$는 MSMCR $Z$로 변환됨
     • 이때 feature analyzer MSMC-VQ-VAE는 $\mathbf{s}$를 직접 모델링하지 않고, mel-spectrogram과 같은 acoustic feature $\mathbf{x}$를 모델링함
     • 해당 module은 loss function $\mathcal{L}_{msmc}$를 최소화하도록 training 된 다음, synthesis와 prediction을 위한 MSMCR $Z$와 codebook group $C$를 제공함 
  2. Synthesis에서 neural vocoder는 MSMCR을 해당하는 speech waveform으로 변환하는 것을 목표로 함
     • 이때 MSMCR sequence는 서로 다른 time resolution을 가지므로 repetition을 통해 동일한 resolution으로 up-sample 된 다음, concatenate 되어 input sequence를 형성함
     • 해당 module은 training set에서 추출된 ground-truth data로 training 된 다음, prediction module에서 예측된 MSMCR $P$로부터 audio를 생성함
  3. Prediction에서 acoustic model은 text sequence $\mathbf{t}$를 multiple sequence의 MSMCR $P$로 변환하는 것을 목표로 함
     • 이때 one-to-one mapping의 기존 acoustic model 보다는 one-to-many acoustic model을 사용해야 함
     • 특히 MSMCR의 latent sequence는 higher stage에서 lower stage로 추출되므로, generation process에서도 해당 pattern을 고려하여 timescale에서 sequence 간의 correlation을 추출해야 함
     • 결과적으로, MSMC-TTS는 text로부터 해당 sequence를 예측하는 acoustic model로써 Multi-Stage Predictor (MSP)를 채택하여 사용

Overall of MSMC-TTS

- Multi-Stage Predictor

• MSP는 non-autoregressive acoustic model인 FastSpeech를 기반으로 함
• Model Architecture
  • MSP는 크게 encoder와 decoder로 구성됨
  • 먼저 text (phoneme) sequence $\mathbf{t}$는 hidden vector $\mathbf{h}_{t}=\mathbf{E}_{t}(\mathbf{t})$로 encoding 된 다음, duration sequence $\hat{\mathbf{d}}=\mathbf{DP}(\mathbf{h}_{t})$에 따라 repition을 통해 upsampling 됨
    - 이때 $\hat{\mathbf{d}}$는 non-negative integer sequence이고, 각 integer는 해당 phoneme이 $\mathbf{x}$에서 지속되는 frame 수
    - $\mathbf{h}_{u}$는 strided convolution layer를 통해 해당하는 stage $\left\{ \mathbf{h}^{(1)}_{d},..., \mathbf{h}_{d}^{(S)} \right\}$에 따라 stage-wise로 downsampling 됨
    
  • Decoder는 highest stage에서 $P$를 예측함
    1. 먼저 $\mathbf{h}_{d}^{(S)}$는 decoder $\mathbf{D}_{S}$에 전달되어 predicted sequence $\tilde{\mathbf{p}}^{(S)}$를 얻은 다음, 해당하는 codebook $\mathbf{c}^{S}$에 의해 $\mathbf{p}^{(S)}$로 quantize됨
    2. Decoder의 last hidden output sequence와 $\mathbf{p}^{(S)}$는 repetition에 의해 upsampling 되고, 다음 decoder $\mathbf{D}_{(S-1)}$의 input으로써 $\mathbf{h}^{(S-1)}_{d}$과 concatenate 됨
    3. 나머지 sequence는 예측된 MSMCR $P$를 형성하기 위해 동일한 방식으로 recursive 하게 생성됨
  • Training 중에는 ground-truth MSMCR $Z$와 ground-truth duration $\mathbf{d}$를 사용할 수 있음
    - 따라서 MSP training을 forcing 하는 teacher를 채택해 $\hat{\mathbf{d}}$를 $\mathbf{d}$로 대체하고, $\left\{ \mathbf{z}^{(S)},..., \mathbf{z}^{(2)} \right\}$를 decoder에 input 함
• Loss Function
  • Input text를 expected codeword에 mapping 하기 위해, MSP는 continuous space에서 직접 codeword를 추정하도록 학습됨
  • 이를 위해, VQ-VAE와 마찬가지로 Euclidean distance를 최소화함:
    (Eq. 14) $\mathcal{L}_{e}=\frac{1}{S}\sum_{i=1}^{S}\mathcal{D}_{e}(\mathbf{p}^{(i)},\mathbf{z}^{(i)})$
    
  • 여기서 input vector $x$와 target codeword $t\in\mathbf{c}$ 사이의 Euclidean distance를 다른 codeword $\mathbf{c}/t = \{w|w\in \mathbf{c}, w\neq t\}$보다 작게 만들기 위해, triplet loss를 추가적으로 채택함
    - 이를 통해 예측된 vector가 expected codeword로 quantize되는 것을 보장할 수 있음
  • 결과적으로, MHVQ와 결합된 triplet loss는:
    (Eq. 15) $\mathcal{D}_{t}(x,t,\mathbf{c})=\frac{1}{M}\sum_{w\in \mathbf{c}/t}\max\left( 0, ||x-t||_{2}^{2}-||x-w||_{2}^{2}+\epsilon\right)$
    $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \mathcal{L}_{t}=\frac{1}{S}\sum_{j=1}^{S}\frac{1}{H}\sum_{k=1}^{H}\frac{1}{L_{j}}\sum_{i=1}^{L_{j}}\mathcal{D}_{t}\left(p_{i}^{(j,k)},z_{i}^{(j,k)},\mathbf{c}^{(j,k)}\right)$
    - $\epsilon$ : margin number로써 constant value
    - 이를 통해 output vector는 target과는 가까워지고, non-target codeword와는 멀리 떨어질 수 있음
  • 그러면 MSP의 final loss function은:
    (Eq. 16) $\mathcal{L}_{msp} =\mathcal{L}_{e} +\gamma \mathcal{L}_{t}$
    - $\gamma$ : weight coefficient

Multi-Stage Predictor

5. Experiments

- Settings

• Dataset : Nancy, CSMSC
• Comparisons : FastSpeech, VITS

- Results

• Standard TTS
  • 기본적인 MOS 품질 측면에서 MSMC-TTS는 가장 우수한 성능을 보임

모델 성능 비교

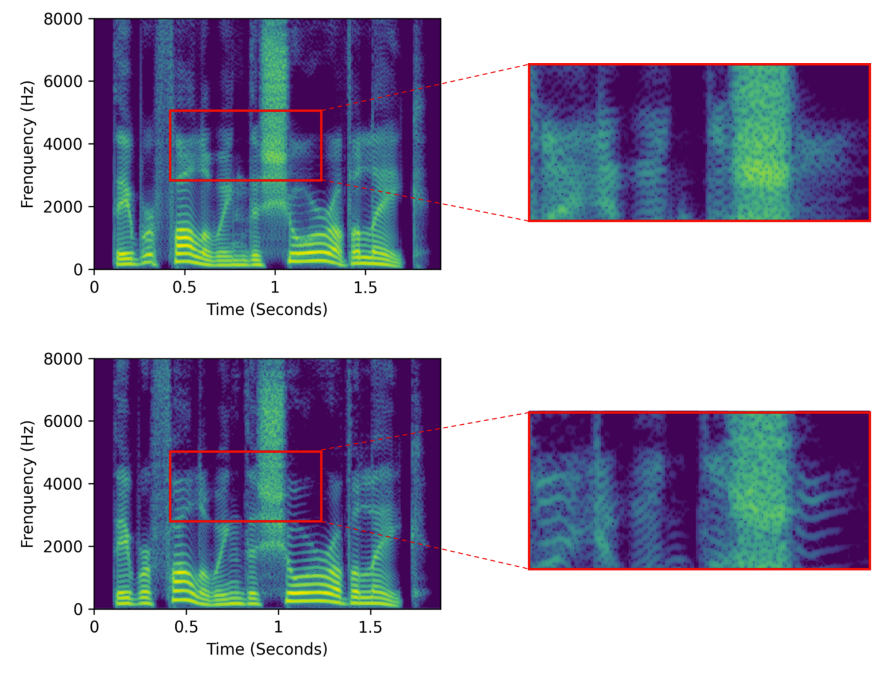
• 각 모델에서 생성된 audio를 비교해 보면 Mel-FS로 생성된 audio는 fuzzy spectrogram을 보임
  - 반면, MSMC-TTS로 생성된 audio는 low-/middle-frequency에서 smooth 하고 clear 한 harmonics를 가짐

생성된 Audio의 Spectrogram 비교 (위) Mel-FS (아래) MSMC-TTS

• 다양한 loss function으로 acoustic model을 training 해보면
  • Cross Entropy는 3.79 MOS로 가장 낮은 성능을 보임
    - 이는 continuous space에서 서로 다른 codework 간의 관계를 고려할 수 없으므로 classification fail 시 smothness의 문제가 나타나기 때문
  • 한편 MSE를 사용하는 경우, 4.13 MOS로 continuous space에서 codeword 추정에 적합함
  • 특히 weight 1의 triplet loss는 4.23 MOS를 달성하여 expressive speech를 합성할 수 있음
    - 여기서 $\gamma=100$과 같이 large weight를 선택하는 경우, 오히려 품질 저하가 발생할 수 있음

Loss function 비교

• Multi-codebook VQ와 multi-stage modeling의 효과를 확인해 보면, One-stage One-codebook (S1C1), One-stage Four-codebook (S1C4), Two-stage Four-codebook (S2C4) 중에서 S2C4가 가장 우수한 성능을 보임

Multi-Codebook, Multi-Stage의 효과

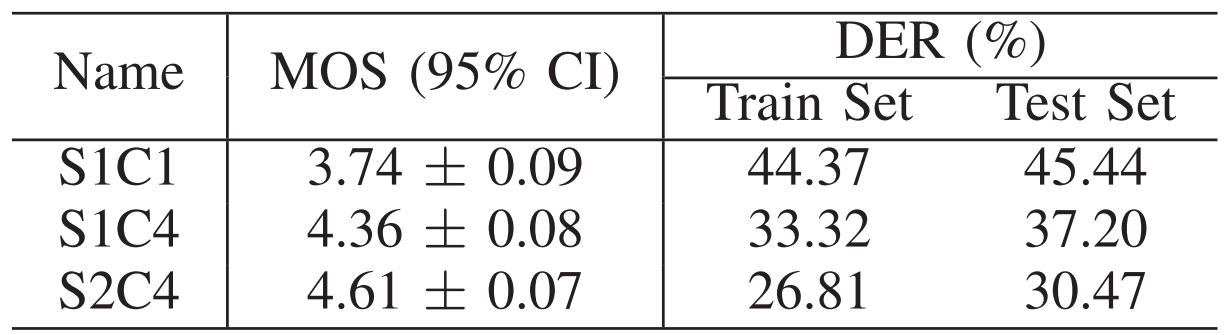
• 추가적으로 S1C1, S2C4로 합성된 audio의 spectrogram을 확인해 보면,
  • Singel-stage TTS의 경우 syllable switching에서 unstable 한 pitch generation이 나타남
  • S2C4의 경우, multi-stage modeling을 통해 다양한 time resolution에서 short-/long-time contextual information을 얻을 수 있음
    - 결과적으로 더 smooth 하고 natural 한 prosody로 이어짐

(좌) S1C1 (우) S2C4

• Resource-Limited Scenarios
  • 먼저 다음의 모델을 구성해 비교해 보면,
    - M1 : 4 layer의 600-dim Transformer block 
    - M2 : 3 layer의 128-dim Transformer block 
    - M3 : 4 layer의 128-dim 1D convolution block 
  • 일반적으로 parameter 수가 줄어들거나 transformer block이 1D CNN으로 대체되는 경우 상당한 MOS 저하가 나타남
  • 반면 MSMC-TTS는 parameter 수가 감소하여도 큰 성능 저하를 보이지 않음

Lightweight TTS

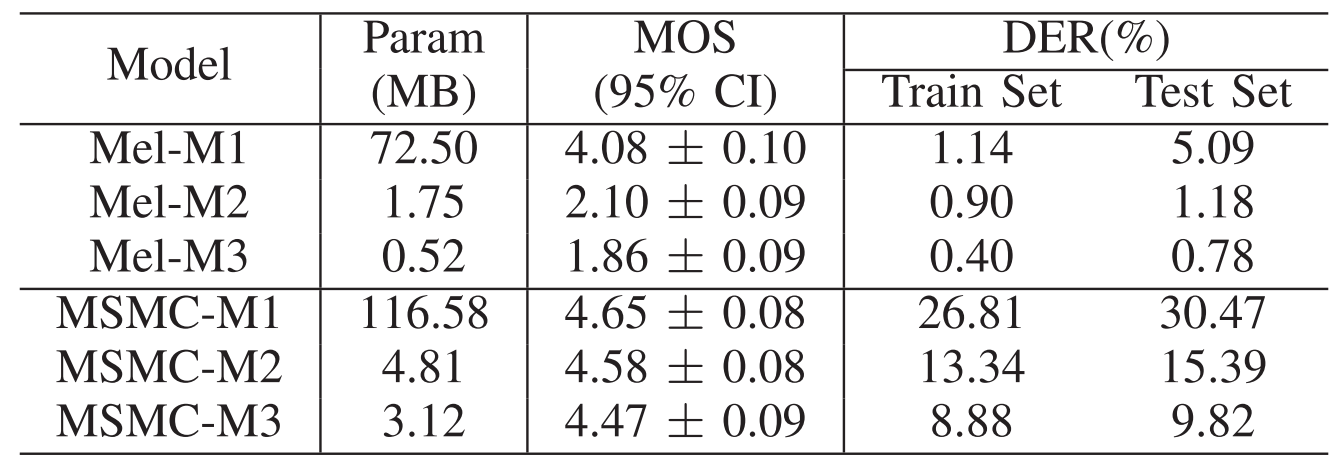
• Low-resource 측면에서
  • 다음의 dataset을 활용해 비교해 보면
    - D1 : 1000 text-audio pair
    - D2 : 1000 text-audio pair + 10000 audio (w/o transcript)
  • 일반적으로 D1 보다 D2를 사용했을 때 더 나은 성능을 보이지만, MSMC-TTS는 D1만을 사용해도 4.59 MOS의 높은 TTS 성능을 보임
    - 즉, MSMC-TTS는 기존 TTS에 비해 data requirement가 더 낮음

Low-Resource TTS

• Synthesis Evaluation
  1. VQ-VAE
     • Single-codebook singe-stage $Z_{1}$은 높은 compactness를 보이지만, reconstruction 측면에서 낮은 성능을 보임
     • $Z_{3}$과 같이 codebook size를 증가시키면 completeness 측면에서 $Z_{1}$보다 소폭 향상된 결과를 얻을 수 있음
       - 즉, codebook size만을 변경하는 것으로는 completness를 control 하는데 한계가 있음
  2. MHVQ
     • MVHQ를 적용하면 head 수에 따라 bitrate가 증가하지만, completness를 크게 향상할 수 있음
     • Codebook size만 증가시킨 $Z_{3}$에 비해 2-head vector quantization을 사용하는 $Z_{5}$는 더 높은 MCD를 달성함

Compactness와 Completness 간의 Trade-off

• 추가적으로 multi-stage representation을 사용하면 target speech에 대한 많은 information을 전달할 수 있음
  

Multi-stage Modeling 비교

• 다양한 representation으로 reconstruct 된 mel-spectrogram을 비교해 보면,
  • High-stage sequence는 coarse-grained, abstract information을 preserve 하는 경향이 있음
  • Low-stage modeling은 low-level, local information을 caputre 하는데 중점을 둠 

Stage별 Mel-spectrogram 비교