티스토리 뷰
반응형
* Python을 기준으로 합니다
최대공약수 (Greatest Common Divisor, GCD)
& 최소공배수 (Least Common Multiple, LCM)
- 개념
- 최대공약수 : 두 수의 약수들 중에서 공통되면서 가장 큰 약수
- 최소공배수 : 두 수의 배수들 중에서 공통되면서 가장 작은 배수
- 기본적으로 최대공약수, 최소공배수 모두 완전 탐색으로 찾을 수 있음
- 최대공약수의 경우 $O(N)$의 time complexity, 최소공배수는 $O(NM)$의 time complexity가 소모됨 - 이때 유클리드 호제법을 활용하면 최대공약수 계산을 $O(\log n)$으로 해결 가능함
- 유클리드 호제법
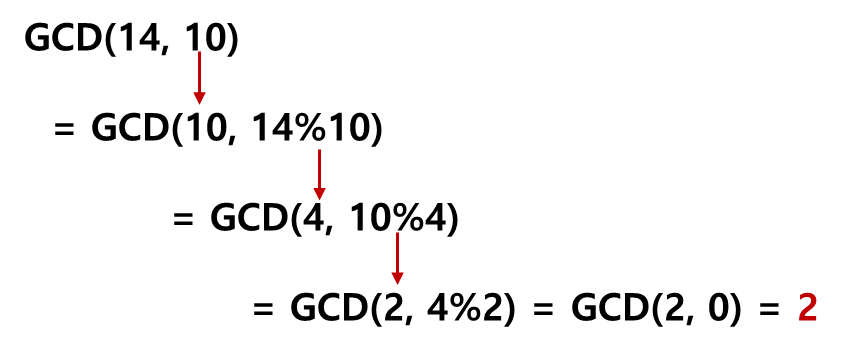
- 두 수 $a, b$ ($a>b$)에 대해, $a$를 $b$로 나눈 나머지를 $r$이라 하면, $a$와 $b$의 최대공약수는 $b$와 $r$의 최대공약수와 같다:
(Eq. 1) $\mathrm{GCD}(a,b) =\mathrm{GCD}(b,r)$
- $r = a%b$이고, $\mathrm{GCD}(a,0)=a$ - 보조적으로 최소공배수는 두 수 $a,b$의 곱을 최대공약수로 나누어 계산할 수 있음:
(Eq. 2) $\mathrm{LCM}(a,b) = (a\times b) / \mathrm{GCD}(a,b)$
- 두 수 $a, b$ ($a>b$)에 대해, $a$를 $b$로 나눈 나머지를 $r$이라 하면, $a$와 $b$의 최대공약수는 $b$와 $r$의 최대공약수와 같다:
- 기본적으로 최대공약수, 최소공배수 모두 완전 탐색으로 찾을 수 있음
- 구현
1. 기본적인 최대공약수, 최소공배수 구하기
- 반복문을 통해 완전 탐색으로 해결 가능함
#최대 공약수
def GCD(N, M):
for i in range(max(N, M), 0, -1):
if N % i == 0 and M % i == 0: #공통적인 약수이면
return i
#최소 공배수
def LCM(N, M):
for i in range(min(N,M), N*M+1):
if i % N == 0 and i % M == 0:
return i
#---------
print(GCD(10, 14)) #2
print(LCM(10, 14)) #702. 유클리드 호제법으로 최대공약수, 최소공배수 구하기
- 유클리드 호제법은 재귀로 구현 가능함
#유클리드 호제법을 통한 최대 공약수
def GCD(N, M):
if M == 0: #GCD(N, 0) = N
return N
else:
return GCD(M, N % M) #GCD(N,M) = GCD(M, N%M)
#최소 공배수
def LCM(N, M):
return (N*M)//GCD(N, M) #최소 공배수 = 두 수의 곱 / 최대 공약수
#---------
print(GCD(10, 14)) #2
print(LCM(10, 14)) #70- 다음과 같이 보다 간략하게 작성할 수도 있음
def GCD(N,M):
while M>0:
N, M = M, N%M
return N
print(GCD(10, 14)) #23. math 라이브러리 활용
- `math` 라이브러리의 `gcd(), lcm()`은 최대공약수, 최소공배수 계산을 지원함
import math
print(math.gcd(10, 14)) #2
print(math.lcm(10, 14)) #70
반응형
'Algorithm' 카테고리의 다른 글
| [Algorithm] 구현 - 시뮬레이션 (0) | 2024.05.09 |
|---|---|
| [Algorithm] 소수 판별 - 밀러-라빈 판정법 (0) | 2024.04.30 |
| [Algorithm] 소수 판별 - 에라토스테네스의 체 (0) | 2024.04.25 |
| [Algorithm] 최장 증가 부분 순열, 최장 공통 부분 수열 (0) | 2024.04.23 |
| [Algorithm] 신장 트리 - 프림 / 크루스칼 알고리즘 (0) | 2024.04.22 |
댓글

