티스토리 뷰
반응형
* Python을 기준으로 합니다
재귀 (Recursion), 분할 정복 (Divide and Conquer)
- 개념
- 재귀 : 자기 자신을 호출하는 것
- 재귀를 활용하면 함수는 시스템적으로 스택에 누적되는데, 해당 스택의 용량에는 한계가 있으므로 일정 횟수 이상을 넘어가면 overflow가 발생함
- Python은 일반적으로 1000의 재귀 상한을 가짐 (`sys.setrecursionlimit()`를 통해 재귀 상한을 늘릴 수 있음) - 반복문 대신 재귀를 사용하는 이유
- 점화식이 존재하는 경우 (e.g. 피보나치 수열, 파도반 수열 등)
- 가독성 향상을 위해 (e.g. DFS)
- 변수 사용을 줄이기 위해
- 점화식이 존재하는 경우 (e.g. 피보나치 수열, 파도반 수열 등)
- 재귀의 사용
- 문제를 해결할 수 있는 점화식 (상태)에 대한 정확한 정의가 필요함
- 재귀 호출이 멈추고 값이 반환되는 종료 조건이 명확해야 함
- 이때 종료조건은 가능한 최대한으로 설정하는 것이 좋음 (e.g. `x == 1 or x== 2` 보다는 `x <= 2`)
- 재귀를 활용하면 함수는 시스템적으로 스택에 누적되는데, 해당 스택의 용량에는 한계가 있으므로 일정 횟수 이상을 넘어가면 overflow가 발생함
- 분할 정복 : 주어진 문제를 해결 가능한 부분 문제로 재귀적으로 나누어 해결한 다음, 해당 결과들을 모아서 원래 문제를 해결하는 방법
- 구현
1. 재귀의 활용 예시
- 프로그래머스 - 콜라츠 추측
- Input : 콜라츠 추측을 계산할 현재 값 `num` / 반복 횟수 `iter`
- Condition : 짝수면 `num//2`, 반복 횟수 증가 / 홀수면 `num*3+1`, 반복횟수 증가
- Terminal : `num == 1`이면 반복횟수 return / `iter == 500`이면 -1 return

def collatz(num, iter):
#종료조건
if num == 1: #결과가 1이면 반복횟수를 return
return iter
if iter == 500: #500번 반복해도 1이 되지 않으면 -1 return
return -1
#recursion
if num % 2 == 0: #짝수면
return collatz(num//2, iter+1) #2로 나누기
else: #홀수면
return collatz(num*3+1, iter+1) #3 곱하고 1 더하기
def solution(num):
answer = collatz(num, 0)
return answer2. 분할 정복을 활용한 거듭제곱 계산
- 일반적인 반복문으로 $x$의 $n$ 거듭제곱을 계산하는 경우 $O(n)$의 time complexity를 소모하지만, 분할 정복을 활용하는 경우 $O(\log n)$으로 개선 가능
- e.g.) $x^{4}$는 $(x^{2})^{2}$로 나눌 수 있고, $x^{2}$는 $(x^{1})^{2}$로 나눌 수 있음
- 분할 정복 적용하기 : 지수 $n$을 절반씩 줄여나가면서 재귀적으로 부분 문제를 구성하고, 결과를 종합하여 최종 거듭제곱 값을 계산
- Terminal : $x^{1}$은 $x$
- 지수 $n$이 짝수이면, $(x^{2})^{n/2}$ 계산
- 지수 $n$이 홀수이면, $x \cdot (x^{2})^{(n-1)/2}$ 계산
def power(x, n):
if n == 1: #종료조건
return x # x^1 = x
elif n%2 == 0: #지수가 짝수면
return power(x*x, n//2) #(x^2)^(n/2)
else: #지수가 홀수면
return x * power(x*x, (n-1)//2) #x * (x^2)^((n-1)/2)
#-------
print(power(2, 10)) #1024- 행렬로 확장 : 위를 $m\times m$ 정방행렬 $X$에 대한 $n$ 거듭제곱 $X^{n}$ 계산으로 확장할 수 있음
#행렬 곱 계산
def multiply(X, Y):
XY = [[0]*len(Y[0]) for _ in range(len(X))]
for i in range(len(X)):
for j in range(len(Y[0])):
for k in range(len(X[0])):
XY[i][j] += X[i][k]*Y[k][j]
return XY
#행렬 거듭제곱 계산
def power(X, n):
if n == 1: #종료조건
return X
elif n%2 == 0: #지수가 짝수면
return power(multiply(X,X), n//2) #(X^2)^(n/2)
else: #지수가 홀수면
return multiply(X, power(multiply(X,X), (n-1)//2)) #X * (X^2)^((n-1)/2)
#--------
X = [[2, 3, 2], [4, 2, 4], [3, 1, 4]] #정방행렬
print(power(X, 10))
'''
[[403686240, 272883424, 460344192],
[541022144, 365719616, 616955392],
[424749920, 287122032, 484364192]]
'''- 계산 결과 확인 : `numpy.linalg`의 `matrix_power()`는 행렬 거듭제곱을 지원함
import numpy as np
X = [[2, 3, 2], [4, 2, 4], [3, 1, 4]] #정방행렬
print(np.linalg.matrix_power(X, 10)) #행렬 거듭제곱 계산
'''
[[403686240, 272883424, 460344192],
[541022144, 365719616, 616955392],
[424749920, 287122032, 484364192]]
'''3. 피보나치 수열
- 피보나치 수열의 점화식은:
(Eq. 1) $\mathrm{fibo}(n) = \left\{\begin{matrix}
0, & n=0 \\
1, & n=1 \\
\mathrm{fibo}(n-2)+\mathrm{fibo}(n-1), & \mathrm{otherwise} \\
\end{matrix}\right.$ - 따라서 반복문 / 재귀를 활용하여 피보나치 수열을 구현할 수 있음
def fibo(n):
if n<=2: #종료조건
return 1
return fibo(n-2)+fibo(n-1)
print(fibo(10)) #55- 이때 꼬리 재귀 (tail recursion)를 통해 연산 없이 결과값을 바로 반환하도록 함으로써 재귀 호출을 개선할 수 있음
def fibo(n, first, second):
if n<=1:
return second
return fibo(n-1, second, first+second) #꼬리 재귀
print(fibo(10,0,1)) #55- 비슷하게, 피보나치 수열은 부분 문제로 나눌 수 있으므로 분할 정복을 활용할 수 있음
- 이때 앞선 거듭제곱 계산, 병합 정렬 등과 달리 피보나치 수열은 같은 부분 문제들이 중복되므로 분할 정복을 사용하면 $O(2^{n})$의 time complexity를 가짐
- 즉, 동일한 부분 문제들이 중복되는 경우 분할 정복은 비효율적일 수 있음
- 이 경우 다이나믹 프로그래밍을 활용하는 것이 좋음
def fibo(n):
if n==0: #종료조건
return 0
elif n==1: #종료조건
return 1
else:
return fibo(n-1)+fibo(n-2)
print(fibo(10)) #55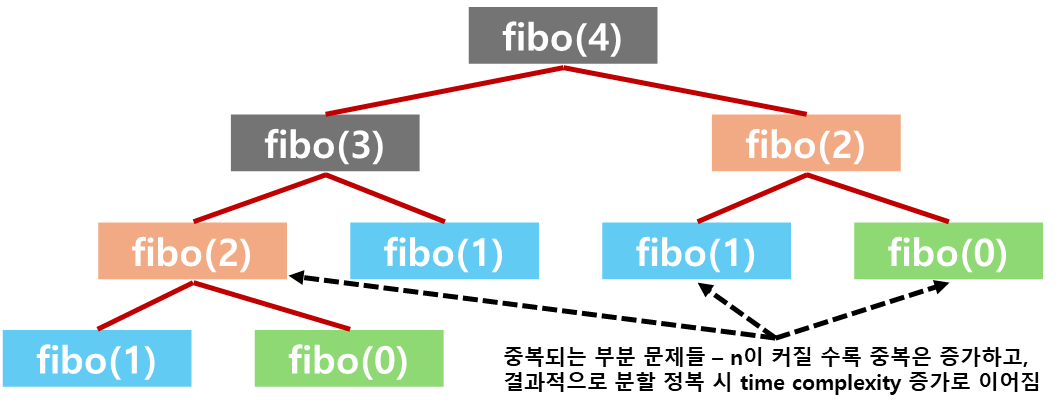
- 한편으로 앞선 행렬 거듭제곱을 활용하면 분할 정복을 기반으로 피보나치 수열을 $O(\log n)$의 time complexity로 해결 가능함
- 이를 위해 피보나치 수열을 $2\times 2$ 정방행렬로 표현하면:
(Eq. 2) $F = \begin{bmatrix}
\mathrm{fibo}(2) & \mathrm{fibo}(1) \\
\mathrm{fibo}(1) & \mathrm{fibo}(0) \\
\end{bmatrix} = \begin{bmatrix}
1 & 1 \\
1 & 0 \\
\end{bmatrix}$ - 해당 행렬에 대한 $n$ 거듭제곱을 계산하여 일반화하면 $n$번째 피보나치 수를 얻을 수 있음:
(Eq. 3) $F^{n} =\begin{bmatrix}
\mathrm{fibo}(2) & \mathrm{fibo}(1) \\
\mathrm{fibo}(1) & \mathrm{fibo}(0) \\
\end{bmatrix}^{n} = \begin{bmatrix}
\mathrm{fibo}(n+1) & \mathrm{fibo}(n) \\
\mathrm{fibo}(n) & \mathrm{fibo}(n-1) \\
\end{bmatrix}$
- 이를 위해 피보나치 수열을 $2\times 2$ 정방행렬로 표현하면:
#행렬 곱 계산
def multiply(X, Y):
XY = [[0]*len(Y[0]) for _ in range(len(X))]
for i in range(len(X)):
for j in range(len(Y[0])):
for k in range(len(X[0])):
XY[i][j] += X[i][k]*Y[k][j]
return XY
#행렬 거듭제곱 계산
def power(X, n):
if n == 1: #종료조건
return X
elif n%2 == 0: #지수가 짝수면
return power(multiply(X,X), n//2) #(X^2)^(n/2)
else: #지수가 홀수면
return multiply(X, power(multiply(X,X), (n-1)//2)) #X * (X^2)^((n-1)/2)
#--------
#행렬 거듭제곱을 활용한 피보나치 계산
def fibo(n):
if n==0:
return 0
elif n==1:
return 1
F = [[1,1],[1,0]] #피보나치 행렬
fibo = power(F, n) #행렬 거듭제곱 계산
return fibo[0][1]
print(fibo(10)) #55반응형
'Algorithm' 카테고리의 다른 글
| [Algorithm] 그리디 (0) | 2024.04.18 |
|---|---|
| [Algorithm] 백트래킹 (0) | 2024.04.16 |
| [Algorithm] 최단 경로 - 플로이드-워셜 알고리즘 (0) | 2024.04.14 |
| [Algorithm] 최단 경로 - 벨만-포드 알고리즘 (0) | 2024.04.11 |
| [Algorithm] 최단 경로 - 다익스트라 알고리즘 (0) | 2024.04.10 |
댓글

