티스토리 뷰
반응형
* Python을 기준으로 합니다
소수 판별 - 에라토스테네스의 체 (Sieve of Eratosthenes)
- 개념
- 소수 : 2보다 큰 자연수 중 1과 자기 자신 만을 약수로 가지는 수
- 기본적으로 완전 탐색을 사용할 수 있지만, $O(n)$의 time complexity가 소모되므로 큰 수에 대해서는 비효율적임
- 이때 자연수의 약수는 대칭적으로 구해진다는 것을 고려하면, $O(\sqrt{n})$의 time complexity로 줄일 수 있음 - 에라토스테네스의 체 : $N$ 보다 작거나 같은 모든 소수를 찾을 때 사용할 수 있고, $O(n \log \log n)$의 time complexity를 가짐
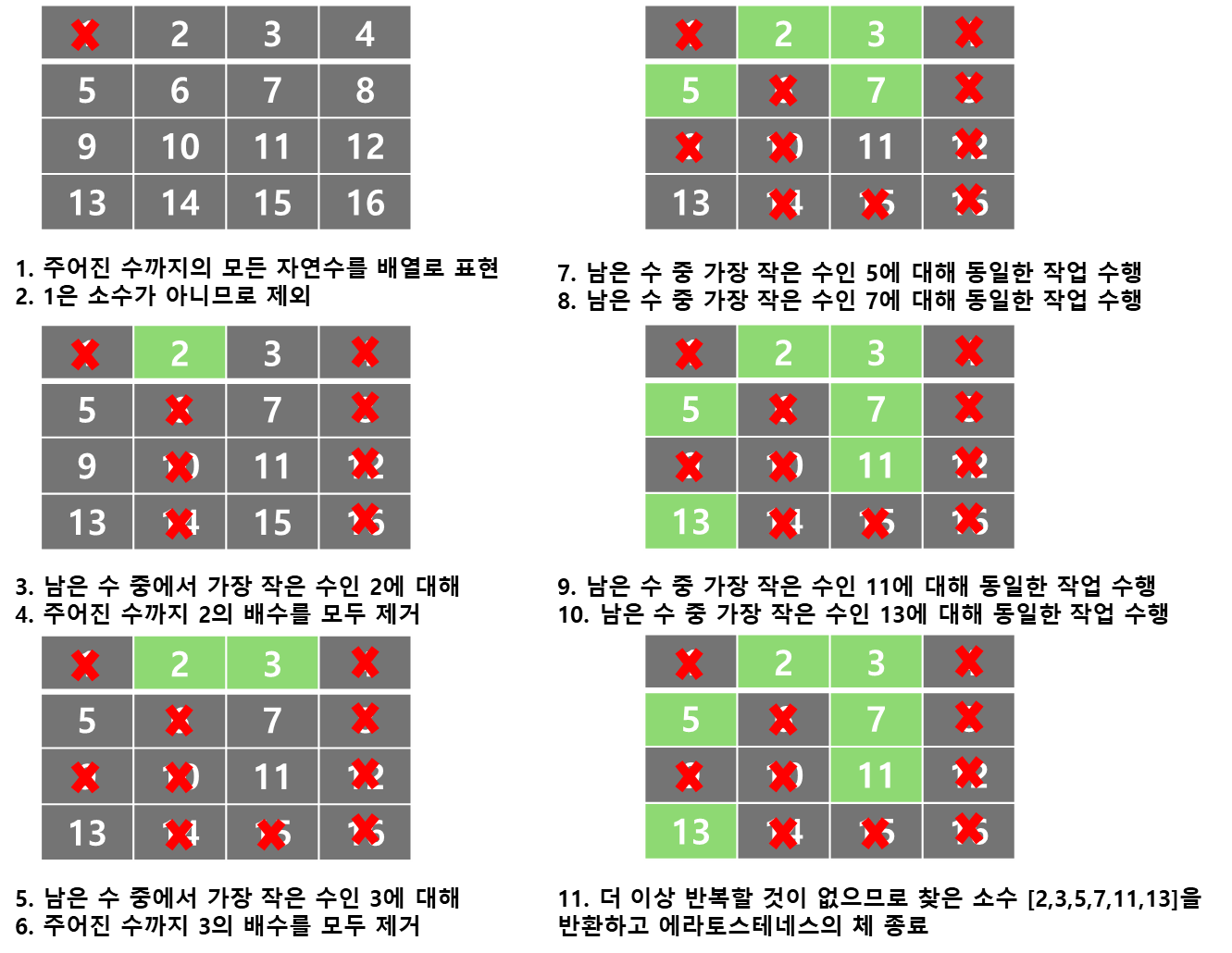
- 에라토스테네스의 체 동작과정
- 2부터 $N$까지의 모든 자연수를 나열
- 남은 수 중에서 처리되지 않은 가장 작은 자연수 $x$을 찾음
- 남은 수 중에서 $x$의 배수를 모두 제거
- 이때 $x$은 제거하지 않음 - 탐색이 끝날 때 때까지 위 2~3번 과정을 반복
- 기본적으로 완전 탐색을 사용할 수 있지만, $O(n)$의 time complexity가 소모되므로 큰 수에 대해서는 비효율적임
- 구현
1. 기본적인 소수 판별법
- 반복문을 통해 주어진 수까지 완전 탐색을 수행하여 소수를 구할 수 있음
def prime_test(x):
for i in range(2, x): #2부터 x-1까지
if x%i == 0: #특정 수의 배수이면
return False #소수가 아님
return True
print(prime_test(12)) #False
print(prime_test(13)) #True- 약수의 대칭성을 활용하면 time complexity를 줄일 수 있음
def prime_test(x):
for i in range(2, int((x**0.5))+1): #2부터 sqrt(x)+1까지
if x%i == 0: #특정 수의 배수이면
return False #소수가 아님
return True
print(prime_test(12)) #False
print(prime_test(13)) #True2. 에라토스테네스의 체를 사용한 소수 판별
- 주어진 수까지의 모든 소수를 찾는데 유용하지만, 메모리를 많이 소모함
def eratos(x):
sieve = [True for i in range(x+1)] #모든 수가 소수(True)인 것으로 체를 초기화
sieve[1] = False #1은 소수가 아님
for i in range(2, int(x**0.5)+1): #2부터 sqrt(x)+1까지
if sieve[i] == True: #i가 소수이면
j = 2
while i*j <= x: #i에서부터 주어진 수 x까지 i의 모든 배수들은
sieve[i*j] = False #소수가 아님
j += 1
return sieve
#------
n = 100
s = eratos(n) #1~100까지의 모든 소수 구하기
for i in range(1, n):
if s[i]:
print(i, end=' ')
#2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
반응형
'Algorithm' 카테고리의 다른 글
| [Algorithm] 소수 판별 - 밀러-라빈 판정법 (0) | 2024.04.30 |
|---|---|
| [Algorithm] 최대공약수, 최소공배수 (0) | 2024.04.26 |
| [Algorithm] 최장 증가 부분 순열, 최장 공통 부분 수열 (0) | 2024.04.23 |
| [Algorithm] 신장 트리 - 프림 / 크루스칼 알고리즘 (0) | 2024.04.22 |
| [Algorithm] 다이나믹 프로그래밍 (0) | 2024.04.19 |
댓글

