티스토리 뷰
반응형
* Python을 기준으로 합니다
최장 증가 부분 수열 (Longest Increasing Subsequence, LIS)
& 최장 공통 부분 수열 (Longest Common Subsequence, LCS)
- 개념
- 부분 수열 : 주어진 수열 중 일부를 뽑아 새로운 수열을 만들 때, 기존의 상대적인 순서를 유지하는 수열
- 최장 증가 부분 수열 (LIS) : 부분 수열의 원소가 오름차순을 유지하면서 가장 길이가 긴 수열
- 일반적으로 다이나믹 프로그래밍으로 해결가능함
- LIS 길이 계산에 다이나믹 프로그래밍 적용하기
- 다이나믹 프로그래밍을 활용하기 위해서는 전체 문제가 중복되는 최적 부분 구조로써 분해 가능해야함
- 최적 부분 구조 : 전체 수열에 대한 LIS 길이는 각 원소로 끝나는 LIS 길이 중 최대값을 구하는 문제와 같음
- 중복 : 이때 각 원소로 끝나는 LIS는 이전 LIS 길이를 참조하여 계산할 수 있음 - 즉, 특정 index의 LIS 길이는 이전에 계산된 LIS 길이들 중, 현재 index에 해당하는 수열의 값보다 작은 수열 값을 가지는 index들에 대한 최대 LIS 길이+1로 계산됨
- 점화식으로 표현하면:
(Eq. 1) $\left\{\begin{matrix}
\mathrm{dp}[1] = 1, & \textrm{terminal condition} \\
\mathrm{dp}[N] = \max(\mathrm{dp}[K])+1, & 1\leq K < N,\, \mathrm{seq}[K]<\mathrm{seq}[N] \\
\end{matrix}\right.$
- 다이나믹 프로그래밍을 활용하기 위해서는 전체 문제가 중복되는 최적 부분 구조로써 분해 가능해야함
- 일반적으로 다이나믹 프로그래밍으로 해결가능함
- 최장 공통 부분 수열 (LCS) : 두 수열의 공통된 부분 수열 중에서 가장 길이가 긴 수열
- LIS와 마찬가지로 다이나믹 프로그래밍으로 해결 가능함
- LCS 길이 계산에 다이나믹 프로그래밍 적용하기
- 두 수열의 원소가 같은지, 같다면 두 원소의 위치가 이전에 찾은 원소의 다음에 있는지를 확인해야 함
- $\mathrm{LCS}(i,j)$를 $x[1,...,i], y[1,...,j]$ 수열의 LCS 길이라고 하자
- $x[i]$와 $y[j]$의 원소가 같을 때 LCS 길이는, $\mathrm{LCS}(i-1, j-1)+1$과 같음
- $x[i], y[j]$의 원소가 다르다면, $\mathrm{LCS}(i-1, j), \mathrm{LCS}(i, j-1)$의 최대값과 같음 - 점화식으로 표현하면:
(Eq. 2) $\left\{\begin{matrix}
\mathrm{LCS}(0,0)=0, & \textrm{terminal condition} \\
\mathrm{LCS}(i-1,j-1)+1, & \textrm{if} \,\, x[i]==y[j]\\
\max(\mathrm{LCS}(i-1, j), \, \mathrm{LCS}(i,j-1)), & \textrm{if} \,\, x[i]\neq y[j] \\
\end{matrix}\right.$
- 구현
1. 최장 증가 부분 수열의 길이 계산
- LIS 길이 계산은 다이나믹 프로그래밍을 활용할 수 있고 $O(n^{2})$의 time complexity를 가짐
def LIS(seq):
n = len(seq)
dp = [1]*n #LCS 길이를 저장할 dp 배열 초기화 (자기 자신의 길이는 1)
for i in range(1, n):
for j in range(i):
#앞에 위치한 수열의 원소들 중 현재 원소(seq[i])보다 작은 경우에 대해 (부분 수열 조건)
if seq[i] > seq[j]:
dp[i] = max(dp[i], dp[j]+1) #최대값으로 LCS 길이 업데이트
return max(dp) #최대 LCS 길이 반환
#-------
s = [1,4,2,3,1,5,6,3]
print(LIS(s)) #5 -> 증가하는 부분 수열 [1,2,3,5,6]의 길이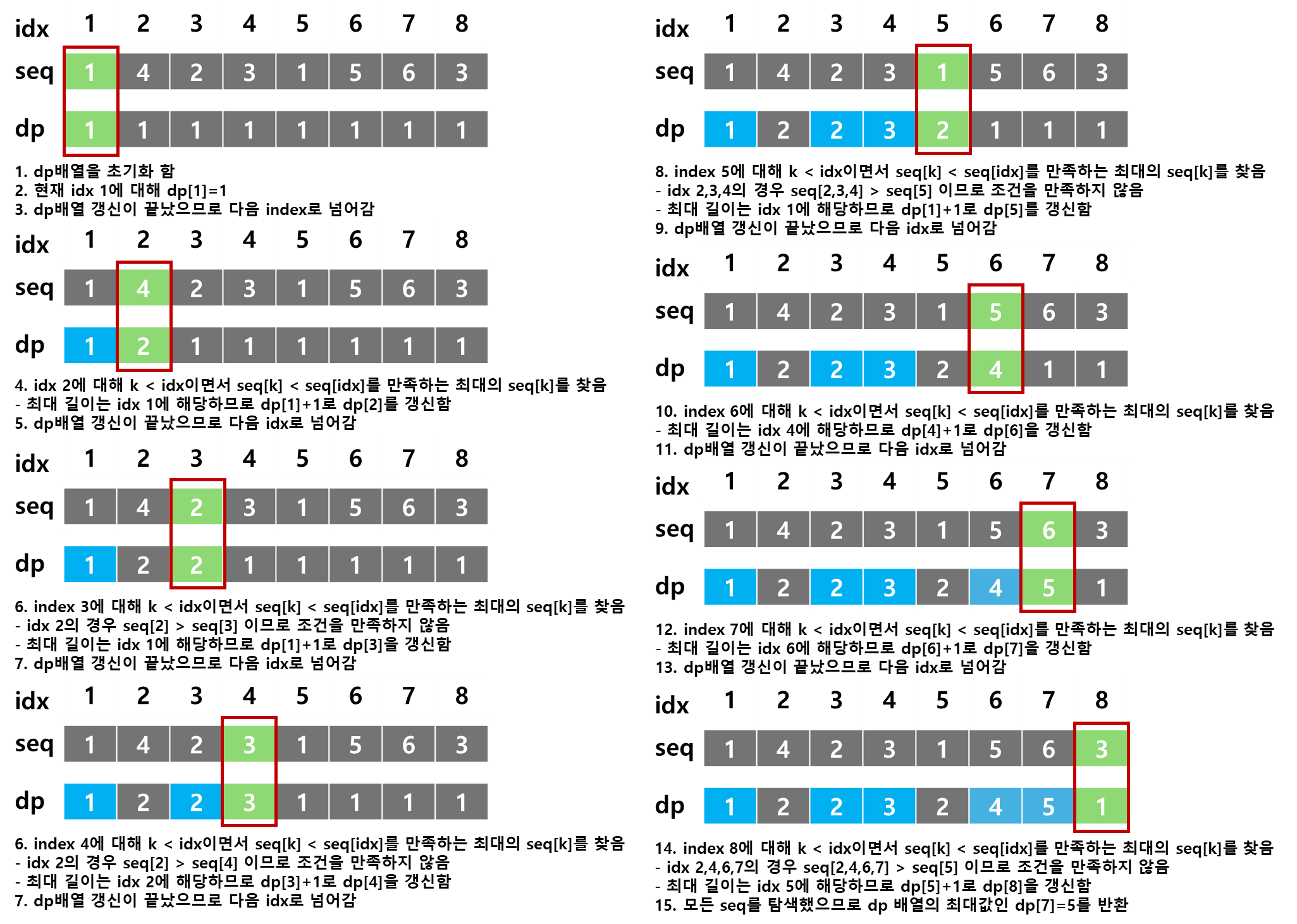
2. 최장 공통 부분 수열의 길이 계산
- LCS 길이 계산도 마찬가지로 다이나믹 프로그래밍을 활용하고, $M, N$ 길이의 각 두 수열에 대해 $O(MN)$의 time complexity를 가짐
def LCS(seq1, seq2):
m = len(seq1)
n = len(seq2)
dp = [[0]*(n+1) for _ in range(m+1)] #dp배열 초기화 (0,0)
for i in range(1, m+1):
for j in range(1, n+1):
if seq1[i-1] == seq2[j-1]: #두 수열의 원소가 같이면
dp[i][j] = dp[i-1][j-1]+1
else: #두 수열의 원소가 다르면
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[m][n], dp #LCS 길이, 역추적을 위한 DP 배열 반환- 이때 앞서 구해진 `dp`배열을 역추적하여 LCS를 구할 수 있음
import collections
def LCS_trace(seq1, seq2, dp):
lcs = collections.deque()
m = len(seq1)
n = len(seq2)
while m > 0 and n > 0:
v = dp[m][n] #dp 배열의 가장 마지막 위치에서 시작
#현재 길이가 이전의 모든 길이들 보다 크면
if v > dp[m][n-1] and v > dp[m-1][n] and v > dp[m-1][n-1]:
m -= 1
n -= 1
lcs.appendleft(seq1[m]) #뒤에서 부터 추적하므로 맨앞에 추가
#현재 길이가 이전 값과 같거나 첫번째 수열에 해당하는 길이보다 큰 경우
elif v == dp[m][n] and v > dp[m-1][n]:
n -= 1 #두번째 수열 위치 이동
else:
m -= 1 #첫번째 수열의 위치 이동
return lcs- 결과 확인
s1 = [1,2,6,4,3,5,7]
s2 = [1,3,2,4,5]
l, dp = LCS(s1, s2)
print(l) #4 : 최장 공통 부분 수열 길이
print(LCS_trace(s1, s2, dp)) #최장 공통 부분 수열 : [1,2,4,5]
반응형
'Algorithm' 카테고리의 다른 글
| [Algorithm] 최대공약수, 최소공배수 (0) | 2024.04.26 |
|---|---|
| [Algorithm] 소수 판별 - 에라토스테네스의 체 (0) | 2024.04.25 |
| [Algorithm] 신장 트리 - 프림 / 크루스칼 알고리즘 (0) | 2024.04.22 |
| [Algorithm] 다이나믹 프로그래밍 (0) | 2024.04.19 |
| [Algorithm] 그리디 (0) | 2024.04.18 |
댓글

