티스토리 뷰
반응형
* Python을 기준으로 합니다
이진 탐색 (Binary Search), 파라메트릭 서치 (Parametric Search)
- 개념
- 이진 탐색 : 정렬된 데이터가 있을 때, 검색 범위를 절반으로 줄여나가면서 값을 탐색하는 방식
- 반드시 정렬된 데이터에서만 사용 가능하지만, $O(\log n)$의 time complexity를 가짐
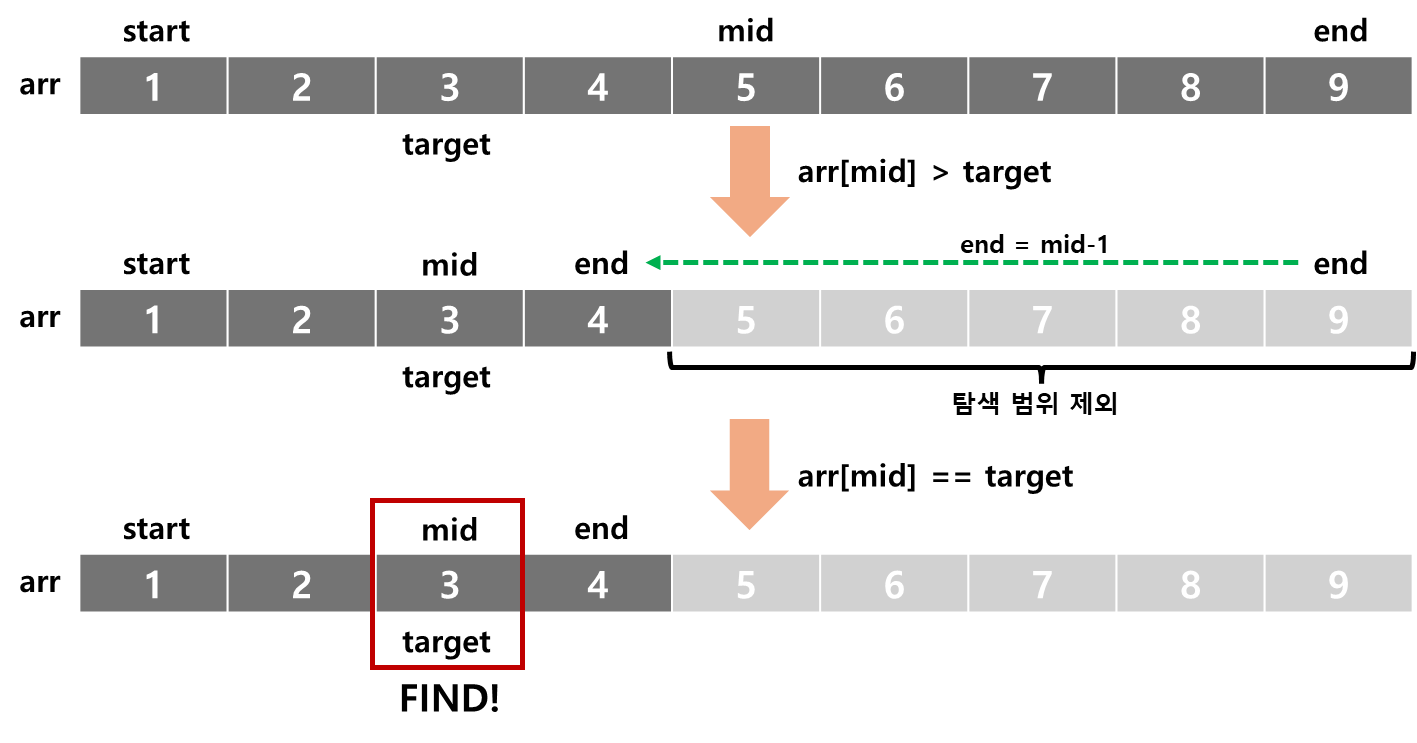
- 이진 탐색의 동작
- 배열의 시작점과 끝을 start, end로 정함
- 가운데를 mid로 정하고, mid에 해당하는 값이 탐색 값이면 탐색을 종료하고 값을 반환
- mid에 해당하는 값이 탐색하려는 값보다 크면 mid의 오른쪽 배열에 대해 이진 탐색 수행, 작으면 mid 왼쪽 배열에 대해 이진 탐색 수행
- 위 2~3 과정을 반복
- 이진 탐색의 응용
- 이진 탐색은 탐색 범위를 계속해서 좁혀나가는 것에 목적이 있으므로, 이 점을 응용하여 직접 탐색 범위와 기준을 정의하고 해당 기준으로 데이터를 탐색할 수도 있음
- mid 포인터를 기준으로하는 탐색 조건을 변형하여 사용하면 됨
- 파라메트릭 서치 : 선택지에 따른 실행 내용을 함수로 만들고, 선택지를 함수의 parameter로 제공하여 값에 따라 Yes/No와 같은 두 갈래의 탐색 방향을 결정하는 방식
- 이때 다음 기준을 만족해야 적용 가능함
- 주어진 선택지에서 최대/최소값을 구할 수 있어야 함
- 위 조건을 만족한다면 다른 작거나 큰 값에서도 최대/최소값을 구할 수 있어야 함 (정렬되어야 함) - 파라메트릭 서치의 동작
- 주어진 선택지 $X$의 범위를 결정하고 start에 $X$의 최소값, end에 $X$의 최대값을 설정
- start, end의 중간인 mid를 찾고, mid가 정답이 될 수 있는지를 판단
- 정답 여부에 따라 start/end를 이동하고, 서로 교차할 때까지 위 과정을 반복
- 예시) 길이가 서로 다른 $K$개의 랜선이 주어질 때, $N$개를 만들 수 있는 최대의 랜선 길이
- 선택지 (랜선의 길이)가 주어지고, 최대의 랜선 길이 (최대값)을 찾는 문제이므로 파라메트릭 서치를 적용 가능함
- 아래 구현 파트의 3. 파라메트릭 서치 활용 참고
- 이때 다음 기준을 만족해야 적용 가능함
- 구현
1. 이진 탐색의 구현
- 반복문을 활용한 구현
def binary_search(arr, target, start, end):
while start <= end:
mid = (start+end) // 2
if arr[mid] == target: #일치하는 값이 있으면
return mid #해당 index 반환
elif arr[mid] > target: # 현재 값이 target보다 작으면
end = mid-1 #mid의 왼쪽 배열 탐색
else: #현재 값이 target 보다 크면
start = mid+1 #mid의 오른쪽 배열 탐색
return None #탐색 결과가 없으면- 재귀를 활용한 구현
def binary_search(arr, target, start, end):
if start > end:
return None #탐색 값이 없으면
mid = (start+end)//2
if arr[mid] == target: #일치하는 값이 있으면
return mid
elif arr[mid]>target: #현재 값이 target보다 작으면 왼쪽 배열 탐색
return binary_search(arr, target, start, mid-1) #recursion
else: #현재 값이 target보다 더 크면 오른쪽 배열 탐색
return binary_search(arr, target, mid+1, end) #recursion- 결과 확인
test = [1, 9, 7, 2, 4, 3, 6, 8, 5]
target = 3
test = sorted(test) #binary search는 정렬된 상태에서만 가능
idx = binary_search(test, target, 0, len(test)-1)
if idx:
print(test[idx]) #3
else:
print('not exist')
#------
target2 = 1000
idx2 = binary_search(test, target2, 0, len(test)-1)
if idx:
print(test[idx2])
else:
print('not exist') #not exist2. bisect 라이브러리를 사용한 이진 탐색의 구현
- `bisect` 라이브러리는 이진 탐색을 지원함
- `bisect_left(배열, target)` : 탐색된 값의 왼쪽 index 반환
- `bisect_right(배열, target)` : 탐색된 값의 마지막 index+1 반환
import bisect
test = [1, 9, 7, 2, 4, 3, 3, 3, 6, 8, 5]
target = 3
test = sorted(test) #binary search는 정렬된 상태에서만 가능
print(test) #[1, 2, 3, 3, 3, 4, 5, 6, 7, 8, 9]
print(bisect.bisect_left(test, 3)) #2 - 배열에서 첫번째 3의 index
print(bisect.bisect_right(test, 3)) #5 - 중복된 값이 있을 때 마지막 index+1을 반환3. 파라메트릭 서치 활용
- 예시 문제 : BOJ 1654 - 랜선 자르기
- 선택지 (랜선의 길이)가 주어지고, 최대의 랜선 길이 (최대값)을 찾는 문제이므로 파라메트릭 서치를 적용 가능함
- 랜선의 길이를 저장할 배열 `lan`을 만들고 start를 최소 길이 $1$, end를 최대 길이 (`lan`의 최대값)으로 설정
- 이진 탐색을 이용하여 start, end의 mid를 계산하고, mid의 정답 여부를 판단함
- mid 만큼 랜선을 자를때 $N$개 이상의 랜선을 만들 수 있다면, mid 보다 더 크게 자를 수 있음 (mid의 오른쪽 탐색)
- 반대로 $N$개의 랜선을 만들 수 없다면, mid 보다 작은 값으로 랜선을 잘라야 함 (mid의 왼쪽 탐색) - 위 과정을 start, end가 교차할 때까지 반복
import sys
input = sys.stdin.readline
K, N = map(int, input().split()) #input 받기
lan = [int(sys.stdin.readline()) for _ in range(K)] #랜선 길이를 저장할 배열
lan = sorted(lan) #이진 탐색은 반드시 정렬되어야 함
start = 1 #랜선 최소길이
end = max(lan) #랜선 최대길이
def binary_search(arr, start,end):
while start <= end:
mid = (start+end)//2
count = 0 #랜선 개수
for x in arr: #랜선 길이 마다 반복
count += x // mid #각 랜선을 mid 길이로 나누었을 때 (잘랐을 때) 랜선의 개수
if count >= N: #N개 이상의 랜선을 만들 수 있다면, mid 보다 더 크게 자를 수 있음
start = mid+1 #mid의 오른쪽 탐색
else: #N개의 랜선을 만들 수 없다면, mid 보다 작은 값으로 랜선을 잘라야 함
end = mid-1 #mid의 왼쪽 탐색
return end
print(binary_search(lan, start, end))반응형
'Algorithm' 카테고리의 다른 글
| [Algorithm] 위상 정렬 (0) | 2024.04.09 |
|---|---|
| [Algorithm] DFS, BFS (0) | 2024.04.08 |
| [Algorithm] 완전 탐색 (0) | 2024.04.05 |
| [Algorithm] 정렬 (0) | 2024.04.04 |
| [Algorithm] 슬라이딩 윈도우 (0) | 2024.04.02 |
댓글

