티스토리 뷰
반응형
* Python을 기준으로 합니다
백트래킹 (Backtracking)
- 개념
- 백트래킹 : 가능성이 없는 해는 포기하여 되돌아가고, 가능성이 높은 해결책만을 탐색하는 방법
- 여러 제약 조건을 만족하는 상태를 탐색해야 하는 제약 충족 문제에 적합한 방식
- 대표적으로 DFS는 더 이상 탐색할 경로가 없으면 (해가 없으면) 되돌아가서 다른 깊이를 탐색하는 방식으로 동작하므로 백트래킹의 예시로 볼 수 있음
- 즉, 백트래킹은 DFS를 기본 골격으로 함 - 백트래킹의 동작
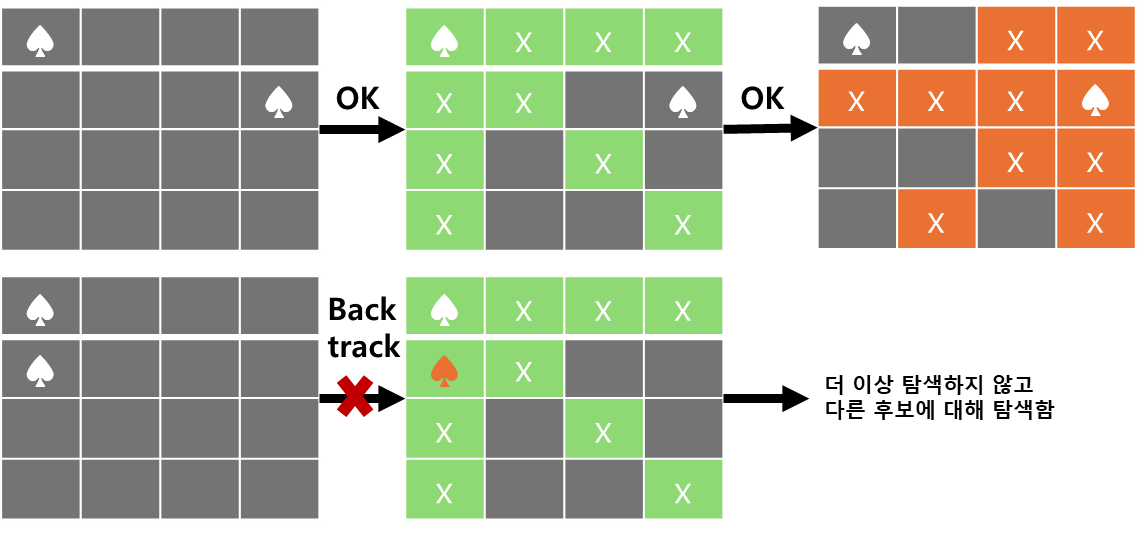
- 가능한 해들의 후보 집합을 정의하고 정의된 집합을 그래프로 표현함
- 이를 상태 공간 트리 (state space tree)라고 함 - 유망 함수를 정의하고,
- 상태 공간 트리를 루트에서부터 DFS로 탐색하면서, 유망 함수에 따라 방문한 노드가 정답이 아니라고 판단되면 더 이상 탐색하지 않고 이전 노드로 돌아가서 다른 해를 탐색함
- 즉, 백트래킹은 상태 공간 트리의 노드들을 가지치기 (pruning)하므로 탐색 효율성을 높일 수 있음
- 가능한 해들의 후보 집합을 정의하고 정의된 집합을 그래프로 표현함
- 주요 예시 : 부분 집합의 합, N-Queen 문제, 스도쿠 등
- 구현
1. N-Queen 문제에 백트래킹 적용하기
- N-Queen 문제 예시 : 프로그래머스 - N-Queen
- $N\times N$ 체스판에 대해 $N$개의 queen을 놓을 때 서로 공격할 수 없는 위치에 배치하는 방법을 탐색하는 문제
- N-Queen 문제는 완전 탐색을 수행하면 $O(N^{N})$의 time complexity를 가지지만, 백트래킹을 적용하면 $O(N!)$로 단축할 수 있음

def nqueen(n, queen, check1, check2, check3):
result = 0
if queen == n: #모든 퀸을 놓을 수 있다면
result += 1
else:
for i in range(n):
#유망 함수 : queen이 추가될 때마다 상하좌우, 양 대각선에 놓을 수 없다면 탐색하지 않음
# == 새로 추가된 queen에 대해 상하좌우, 양 대각선에 놓을 수 있다면 탐색함
if not check1[i] and not check2[i+queen] and not check3[i-queen+n]:
#현재 위치에서 새로운 queen을 놓을 수 없는 위치를 True로 업데이트
check1[i] = True
check2[i+queen] = True
check3[i-queen+n] = True
result += nqueen(n, queen+1, check1, check2, check3) #다음 queen을 계산
#백트래킹 되면 해당 위치 초기화
check1[i] = False
check2[i+queen] = False
check3[i-queen+n] = False
return result
def solution(n):
check1 = [False]*n #상하좌우
check2 = [False]*(n*2) #대각선1
check3 = [False]*(n*2) #대각선2
return nqueen(n, 0, check1, check2, check3)2. 백트래킹 응용
- 문제 예시 : 프로그래머스 - 피로도
- Input : 현재 피로도 `k`, 배열 `dungeon` : [최소 필요 피로도, 소모 피로도] 형태
- 현재 피로도 `k`가 던전의 $i$번째 던전의 최소 필요 피로도 `dungeon[i][0]`보다 낮으면 백트래킹하면 되는 문제
- 현재 피로도가 던전의 최소 피로도보다 크거나 같으면 탐색하는 것과 동치

def backtrack(k, count, dungeons, check):
result = count
for i in range(len(dungeons)): #던전 만큼 반복
#현재 피로도가 던전의 최소 필요 피로도보다 크거나 같고, 탐색하지 않은 던전이라면 탐색함
if k >= dungeons[i][0] and not check[i]:
check[i] = True #던전 탐색
#현재 탐색한 던전 수와 추가 탐색했을 때 던전 수 중에서 최대값으로 갱신
result = max(result, backtrack(k-dungeons[i][1], count+1, dungeons, check))
check[i] = False #백트래킹 되면 던전 탐색 취소
return result
def solution(k, dungeons):
check = [False]*len(dungeons) #던전 탐색 여부
answer = backtrack(k, 0, dungeons, check)
return answer
반응형
'Algorithm' 카테고리의 다른 글
| [Algorithm] 다이나믹 프로그래밍 (0) | 2024.04.19 |
|---|---|
| [Algorithm] 그리디 (0) | 2024.04.18 |
| [Algorithm] 재귀, 분할 정복 (0) | 2024.04.15 |
| [Algorithm] 최단 경로 - 플로이드-워셜 알고리즘 (0) | 2024.04.14 |
| [Algorithm] 최단 경로 - 벨만-포드 알고리즘 (0) | 2024.04.11 |
댓글

