티스토리 뷰
반응형
* Python을 기준으로 합니다
최단 경로 - 다익스트라 (Dijkstra) 알고리즘
- 개념
- 다익스트라 알고리즘 : 그래프의 최단 경로를 찾기 위한 알고리즘 중 하나로, BFS를 기반으로 가장 비용이 적은 노드만을 선택하는 그리디 방식으로 동작함
- 그래프에서 간선의 가중치가 모두 양수라는 조건하에서 사용 가능함
- 다익스트라 알고리즘은 각 노드에 대한 최단 거리를 배열 저장하고 계속 갱신한다는 특징이 있음 - 다익스트라 알고리즘의 동작 과정
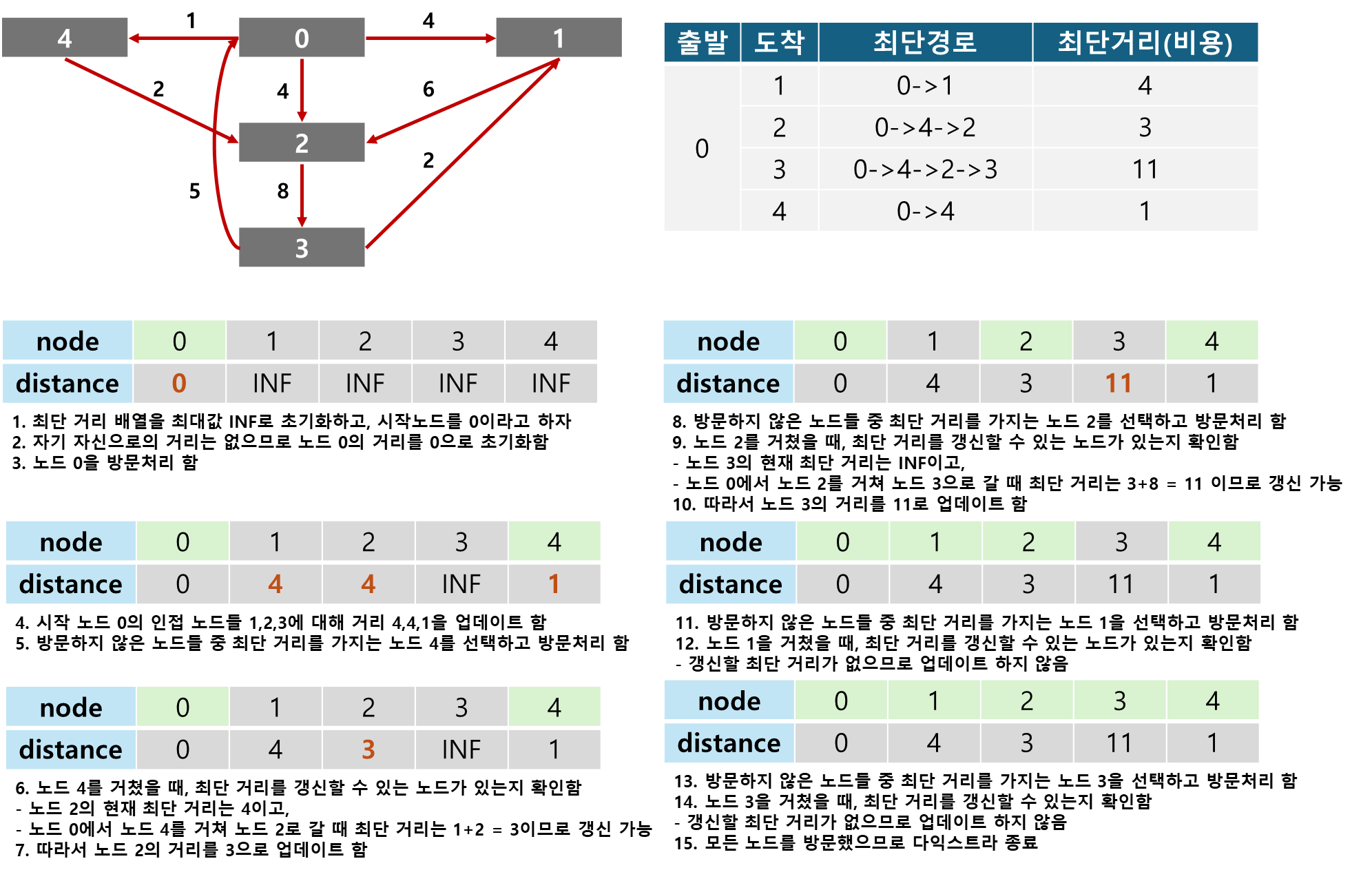
- 시작 노드를 설정하고, 최단 거리를 저장할 배열을 매우 큰 값(INF)으로 초기화함
- 방문하지 않은 노드 중에서 가장 최단 거리(최소 비용)를 가진 노드를 선택함
- 해당 노드를 거쳐 다른 노드로 가는 최단 거리를 계산하고, 현재까지 구한 최단 거리와 비교하여 작은 값으로 최단 거리 배열을 갱신함
- 위 2~3 과정을 반복
- Time Complexity
- 기본적인 다익스트라 알고리즘은 $V$개의 노드에 대해 $O(V^{2})$의 time complexity를 가짐
- 우선순위 큐를 활용하여 개선된 다익스트라 알고리즘은 $V$개의 노드, $E$개의 간선에 대해 $O(E \log V)$를 보장함
- 그래프에서 간선의 가중치가 모두 양수라는 조건하에서 사용 가능함
- 구현
1. 기본적인 다익스트라 알고리즘의 구현
- 최단 거리를 저장하는 배을 선언한 다음, 각 단계마다 방문하지 않은 노드 중에서 가장 짧은 최단 거리를 가진 노드를 선택함
- 이때 노드 선택을 위해 최단 거리 배열을 순차 탐색함
import sys
INF = sys.maxsize #최대값
def shortest_path(distance, visited):
min_val = INF
idx = 0
for i in range(5): #노드개수 만큼
if distance[i] < min_val and not visited[i]:
min_val = distance[i]
idx = i
return idx
def dijkstra(graph, start):
distance = [INF] * 5
visited = [False] * 5
# 시작 노드 초기화
distance[start] = 0
visited[start] = True
for node, cost in graph[start]:
distance[node] = cost # 시작 노드의 인접 노드에 대한 거리 업데이트
for _ in range(5-1): #노드개수 -1 만큼
cur = shortest_path(distance, visited) # 가장 짧은 거리인 노드를 찾아서
visited[cur] = True # 방문 처리
for node, cost in graph[cur]: #해당 노드의 인접 노드에 대해
new_cost = distance[cur] + cost
if new_cost < distance[node]: # 기존 거리보다 더 짧은 거리가 있으면
distance[node] = new_cost #최단 거리 갱신
return distance- 결과 확인
#인접 리스트 형식 그래프
graph = [
[(1,4),(2,4),(4,1)],
[(2,6)],
[(3,8)],
[(0,5),(1,2)],
[(2,2)]
]
#0에서 시작했을 때 최단거리
print(dijkstra(graph, 0)) #[0, 4, 3, 11, 1]2. 우선순위 큐를 활용한 다익스트라 알고리즘의 개선
- 최단 거리 배열에 대한 순차 탐색 과정에서 소모되는 time complexity를 우선순위 큐를 사용해 개선함
- 최소힙의 특징을 활용하여 앞선 기본 다익스트라 구현의 `shortest_path()` 함수 부분을 대체할 수 있음
import heapq #우선순위 큐는 힙을 사용함
def dijkstra(graph, start):
prique = [] #우선순위 큐
distance = [INF] * 5 #거리 초기화
#시작 노드 초기화
heapq.heappush(prique, (0, start)) #시작 노드를 우선순위 큐에 push
distance[start] = 0
while prique:
#기본 다익스트라 구현의 shortest_path()를 대체하는 부분
dist, cur = heapq.heappop(prique) #우선순위 큐 pop을 통해 가장 짧은 거리인 노드를 찾음 (최소힙의 특징)
#이미 방문한 노드면
if distance[cur] < dist:
continue
#해당 노드의 인접 노드에 대해
for node, cost in graph[cur]:
new_cost = dist + cost
if new_cost < distance[node]: # 기존 거리보다 더 짧은 거리가 있으면
distance[node] = new_cost #최단 거리 갱신
heapq.heappush(prique, (new_cost, node)) #갱신된 최단거리와 노드를 우선순위 큐에 push
return distance- 결과 확인
graph = [
[(1,4),(2,4),(4,1)],
[(2,6)],
[(3,8)],
[(0,5),(1,2)],
[(2,2)]
]
#0에서 시작했을 때 최단거리
print(dijkstra(graph, 0)) #[0, 4, 3, 11, 1]반응형
'Algorithm' 카테고리의 다른 글
| [Algorithm] 최단 경로 - 플로이드-워셜 알고리즘 (0) | 2024.04.14 |
|---|---|
| [Algorithm] 최단 경로 - 벨만-포드 알고리즘 (0) | 2024.04.11 |
| [Algorithm] 위상 정렬 (0) | 2024.04.09 |
| [Algorithm] DFS, BFS (0) | 2024.04.08 |
| [Algorithm] 이진 탐색, 파라메트릭 서치 (0) | 2024.04.06 |
댓글

