[Paper 리뷰] SpatialCodec: Neural Spatial Speech Coding

SpatialCodec: Neural Spatial Speech Coding

---

• Multi-channel recording에 embed 된 spatial cue를 정확하게 reconstruct 하고 preserve 하기 위한 효과적인 encoding 방식이 필요함
• SpatialCodec
  • Single-channel neural sub-band와 SpatialCodec의 two phase로 구성된 neural audio coding framework  
  • Neural sub-band codec은 low bitrate로 reference channel을 encode 하고
  • SpatialCodec은 decoder end에서 정확한 multi-channel reconstruction을 위해 relative spatial information을 capture 함
• 논문 (ICASSP 2024) : Paper Link

---

1. Introduction

• Audio/Speech codec은 signal을 낮은 bitrate code로 compressing 하는 것을 목표로 함
  • 일반적으로는 signal model이나 psycho-acoustic을 활용하여 수행됨
    - CLEP, SPEEX, OPUS 등의 codec은 linear predictive modeling을 활용하고 MP3는 perceptual coding을 활용함
    - BUT, 이러한 기존 방식들은 매우 낮은 bitrate로 인해 reconstruction 성능의 한계가 있음
  • Neural codec은 기존 codec들의 낮은 bitrate에서의 고품질 reconstruction 문제를 해결 가능함
    - 대표적으로 SoundStream은 residual vector quantization (RVQ)를 활용하고, EnCodec은 transformer를 활용하여 code 분포를 모델링함
  • 이러한 neural codec은 주로 VQ-VAE나 GAN-based vocoder를 활용하여 구조적으로 파생됨
    - 따라서 해당 codec으로 얻어지는 encoded information은 generation task에서 learned representation으로 사용할 수도 있음

• 한편으로 spatial audio codec은 spatial information을 preserve 하면서 multi-channel audio를 compress 하는 것을 목표로 함
  • 이와 같은 multi-channel codec은 MPEG-3D audio, MPEG-Surround와 같이 playback/multi-speaker system에서 활용됨
  • 이때 spatial audio codec은 다음의 pipeline으로 주로 구성됨
    1. Multi-channel audio를 mono/stereo로 downmix 하고 기존 audio codec으로 code 함
    2. 일부 sub-band spatial parameter가 multi-channel audio로부터 추출되어 channel-wise, band-wise로 code 됨
    3. 이후 decoder는 앞선 2가지 component의 multi-channel audio를 resynthesize 함
  • 이러한 기존의 spatial codec은 특정한 playback system만을 고려하고 inter-channel/inter-band correlation을 fully exploit 하지 못함
    - 따라서 적절한 reconstruction을 위해서는 system이 각 channel에 대해 개별적으로 coding 된 large band를 가져야 하므로, coding bitrate가 높아져야 함

-> 그래서 neural network를 사용하여 coding bitrate 문제를 해결하는 SpatialCodec을 제안

 

• SpatialCodec
  • SpatialCodec은 기존 방법들과 비슷하게 two-branch로 구성됨
    1. First branch에서는 reference channel audio를 coding 하고
    2. Second branch는 spatial information을 coding 함
  • Decoder 측면에서 first branch의 decoder는 reconstructed reference channel을 output 함
    - 이후 second branch의 decoder output과 reconstructed reference channel을 함께 사용하여 모든 non-reference channel을 합성함
  • 추가적으로 spatial cue preservation을 evaluation 하기 위한 몇 가지 metric을 제시함
    - Ground-truth spatial feature에 대한 cosine similarity를 계산하는 Spatial Similarity
    - Spectral quality와 main directivity에 대한 beamforming performance (PESQ, SNR, STOI)

< Overall of SpatialCodec >

• Single-channel neural sub-band와 SpatialCodec의 two-branch로 구성된 neural audio coding framework  
• First branch에서는 low bitrate로 reference channel을 encode 하고, Second branch는 정확한 multi-channel reconstruction을 위해 relative spatial information을 capture 함
• 결과적으로 12kpbs의 bitrate만으로 96kps의 기존 방식보다 뛰어난 성능을 달성

2. Problem Formulation

• 논문은 reverberant 환경에서 $M$-channel microphone array의 spatial audio recording을 compress 하는 문제를 고려함
  • 우선 $s(t)$와 $h_{i}(t)$를 각각 speaker의 clean speech와 speaker에서 $i$-th microphone까지의 Room Impulse Response (RIR)이라 하자
    1. 그러면 $M$-channel microphone array에 의해 caputre 된 mixture signal $\mathbf{x}(t)$는 time $t$에 대해 다음과 같이 정의됨:
       (Eq. 1) $\mathbf{x}(t)=[h_{1}(t),...,h_{M}(t)]*s(t)$
       - $*$ : convolution operation
    2. $\mathbf{x}(t) = [x_{1}(t),...,x_{M}(t)]$에는 speaker의 direct path에서 capture 한 음성과 $M$-channel array를 사용한 early, late reflection이 포함됨
  • 이때 SpatialCodec의 목표는 $\mathbf{x}$를 low bitrate representation $\mathbf{C}$로 compress 했을 때, decoder에서 reconstruct 되는 multi-channel audio $\hat{\mathbf{x}}$가 모든 spatial cue를 preserve 하는 것
    - 이를 위해 SpatialCodec은 encoder $\Psi_{Enc}$, quantizer $\Psi_{Quant}$, decoder $\Psi_{Dec}$로 구성됨
  • 결과적으로 $\hat{\mathbf{x}}$는 spectral (perceptual quality)와 spatial (direct path, early, late reflection) 모두에서 $\mathbf{x}$에 근사하도록 jointly optimize 됨:
    (Eq. 2) $\hat{\mathbf{x}}=\Psi_{Dec}(\mathbf{C}); \,\, \mathrm{where}\,\, \mathbf{C}=\Psi_{Quant}(\Psi_{Enc}(\mathbf{x}))$

3. Method

• SpatialCodec의 architecture는 크게 two-branch로 구성됨
  1. Microphone array의 reference channel을 coding 하기 위해 pre-train 된 single-channel sub-band codec
  2. Multi-channel audio signal을 reconstruct 하기 위해 spatial information을 coding 하는 SpatialCodec

- Single-Channel Sub-band Codec (First Branch)

• Reference channel sub-band codec은 neural frequency-domain sub-band codec과 같음
  • Input $x_{ref}\in \mathbb{R}^{2\times T\times F}$는 reference channel audio의 STFT이고, 여기서 $2$는 실수/허수부에 해당함
    
  • 전체 encoder-decoder architecture는 실수-허수를 channel dimension으로 처리하는 residual block이 포함된 2D-CNN으로 구성
    1. 해당 architecture는 1D-CNN이 2D-CNN으로 대체되고, downsampling time이 downsampling frequency가 된다는 점을 제외하면 HiFi-Codec과 동일함
    2. Encoder, decoder 모두 6개의 convolution layer를 가지고, 각 layer 다음에 residual unit이 추가됨
       - Encoder의 경우, time dimension에 대한 6개 layer의 kernel, stride는 각각 3과 1
       - Frequency dimension의 kernel, stride는 각각 $[5,3,3,3,3,4], [2,2,2,2,1]$
       - 모든 layer의 output channel size는 $[16, 32, 64, 128, 128, 256]$
    3. 여기서 640 point FFT를 사용하여 encoder가 frequency dimension을 321에서 6개의 convolutional sub-band로 compress 하도록 함
       - 이후 residual vector quantization을 사용하여 해당 6개의 sub-band를 independently code 함
       - 이때 decoder는 encoder의 반대로 구성됨
  • 각 residual unit에는 2개의 residual block이 포함되고, 각 block에는 skip connection이 있는 3개의 2D time-dilated CNN layer가 존재함
    - 첫 번째 block의 kernel, dilation size는 (time, freq) 순서로 각각 $[(3,3), (3,5), (3,5)], [(1,1), (3,1), (5,1)]$
    - 두 번째 block의 kernel, dilation size는 $[(7,3),(7,5),(7,5)], [(1,1), (3,1),(5,1)]$

- SpatialCodec (Second Branch)

• SpatialCodec은 6개의 convolution layer에 대한 input, output, channel dimension을 제외하고 앞선 reference channel codec과 동일한 구조를 가짐
  • 먼저 SpatialCodec의 input은 reference channel STFT와 channel dimension으로 concatenate 된 spatial covariance를 사용함
    1. $M$-channel STFT $\mathbf{X}(t,f)\in \mathbb{C}^{M\times 1}$이 주어졌을 때, spatial covariance matrix $\Phi(t,f)\in \mathbb{C}^{M\times M}$은:
       (Eq. 3) $\Phi(t,f)=\mathbf{X}(t,f)\mathbf{X}(t,f)^{H}$
    2. 이후 $\Phi(t,f)$의 실수부와 허수부는 reference channel STFT의 실수부, 허수부와 concatenate 되어 각 time-frequency bin에 대해 $2(M^{2}+1)$ dimensional 실수 feature를 제공함
       - 그리고 해당 feature는 SpatialCodec에 feed 될 때, channel dimension으로 처리됨
  • Encoder의 모든 layer에 대한 output channel dimension은 $[128,128,128,128,256,256]$
    - Spatial decoder의 경우 output은 모든 non-reference channel에 대한 Complex Ratio Filter (CRF) $W_{m}(t,f)\in \mathbb{C}^{2L+1,2K+1},\, m\in [1,...,M-1]$
    - 이때 CRF는 spatial relative transfer function을 encode 함
  • Reference channel STFT의 output이 $\hat{X}_{ref}\in\mathbb{C}^{T\times F}$라고 하면, $m\in [1,...,M-1]$에 대한 모든 non-reference channel은:
    (Eq. 4) $\hat{X}_{m}^{\textrm{non_ref}}(t,f)=\sum_{l=-L}^{L}\sum_{k=-K}^{K}W_{m}(t,f,l,k)\hat{X}_{ref}(t+l,f+k)$
    - 따라서 last layer의 spatial decoder output channel dimension은 $2\times (2L+1) \times (2K+1) \times (M-1)$
    

Overall of SpatialCodec

- Training and Loss

• First branch의 training loss는 HiFi-Codec의 방식을 따라, reconstruction loss, adversarial loss, codebook learning loss로 구성됨
  • 여기서 weight $\lambda=5$의 time-domain SNR loss를 추가로 사용하고, 이때 SNR loss는:
    (Eq. 5) $L_{SNR}(x,\hat{x})\triangleq -10\log_{10}\left(\frac{||x||^{2}}{||x-\hat{x}||^{2}}\right)$
    
  • Second branch는 first branch와 개별적으로 training 되고, training 중에 Complex Ratio Filter (CRF)는 first branch에서 reconstruct 된 reference channel 대신 original reference channel audio에 적용됨
    1. 이는 pre-training 이후에도 first branch는 기존 음성과 perceptually equivalent 한 reconstructed speech를 output 할 수 있기 때문
       - 그러면 underlying spectrogram이나 waveform이 exact match 되지 않음
    2. 결과적으로 reconstructed speech에 CRF를 적용하면, first branch의 mismatching 문제로 인해 original non-reference channel audio를 learning target으로 사용할 수 없음
  • 따라서 training 중에는 (Eq. 4)와 달리 다음을 사용함:
    (Eq. 6) $\hat{X}_{m}^{\textrm{non_ref}}(t,f)=\sum_{l=-L}^{L}\sum_{k=-K}^{K}W_{m}(t,f,l,k)X_{ref}(t+l,f+k)$
    - $\hat{X}_{ref}$는 original reference channel signal $\hat{X}_{ref}$를 대체
  • 그런 다음, 모든 non-reference channel에 대해 평균화된 time-domain SNR loss를 적용함:
    (Eq. 7) $L_{all}=\frac{1}{M-1}\sum_{m=1}^{M-1}L_{SNR} \left(\mathrm{ISTFT}(X_{m}^{\textrm{non_ref}}), \mathrm{ISTFT}(\hat{X}_{m}^{\textrm{non_ref}}) \right)$

- Inference

• 추론 시에는 (Eq. 4)를 사용하여 $\hat{X}_{m}^{\textrm{non_ref}}$를 얻음
  1. First branch의 sub-band codec은 reference channel audio를 reconstruct 하고,
  2. 이후 second branch의 SpatialCodec은 $M-1$ complex ratio filter를 reconstruct 하여 $M-1$ non-reference channel audio를 reconstruct 함

4. Experiments

- Settings

• Dataset : AISHELL-2
• Comparisons : HiFi-Codec, EnCodec

- Results

• Overall Comparisons
  • SpatialCodec은 12kpbs의 bitrate만으로 다른 높은 bitrate를 사용하는 모델들보다 더 나은 성능을 달성함
  • 특히 각 channel이 적절한 coding rate로 code 되더라도 channel-independent (CI) coding은 spatial information을 잘 preserve 하지 못함

Audio reconstruction 실험 결과

• Spatial Performance
  • DoA error 측면에서 SpatialCodec은 EnCodec과 결합할 때, 가장 우수한 성능을 보임
  • RTF error의 경우, SpatialCodec은 sub-band codec과 결합했을 때 최고의 성능을 발휘함
  • Spatial Similarity (SS) 측면에서 SpatialCodec은 reference channel codec과 결합했을 때 0.95의 높은 성능을 달성함
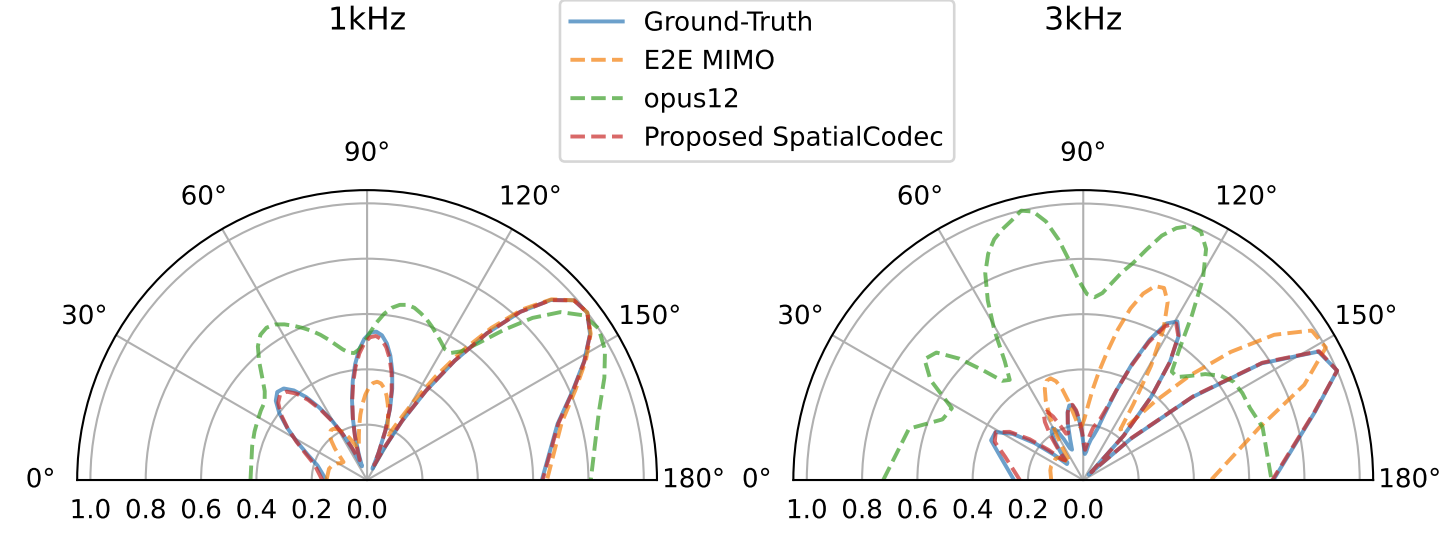
• SpatialCodec을 포함한 각 codec들의 $B=50$ normalized spatial feature를 확인해 보면
  • SpatialCodec은 1kHz, 3kHz frequency 모두에서 ground-truth와 상당히 align 되는 결과를 보임
  • 반면 OPUS12와 MIMO E2E는 ground-truth pattern과 상당한 차이를 보임
  • 결과적으로 spatial performance 측면에서 SpatialCodec은 reference channel codec과 결합될 때 뛰어난 성능을 달성할 수 있음

Spatial Feature Visualization

• Beamforming Performance
  • SpatialCodec은 intrusive, non-intrusive beamforming metric에 대해 모두 좋은 결과를 보임
    - 즉, 뛰어난 spectral reconstruction 성능을 보임
  • 실제로 PESQ, STOI, SNR 모두에서 SpatialCodec은 기존 방식들보다 우수한 성능을 보임