[Paper 리뷰] Pruning Self-Attention for Zero-Shot Multi-Speaker Text-to-Speech

Pruning Self-Attention for Zero-Shot Multi-Speaker Text-to-Speech

---

• Personalized speech generation을 위해서는 target speaker의 limited data를 사용해서 Text-to-Speech를 수행해야 함
• 이를 위해 text-to-speech 모델은 out-of-domain data에 대해 amply generalize 되어야 함
• Self-Attention Pruning
  • Generalization을 위해 text-to-speech 모델의 transformer에 대해 spase attention을 통한 pruning을 적용
  • Attention weight가 threshold 보다 낮은 self-attention layer에서 redundant connection을 pruning
  • 이때 pruning strength를 결정하기 위해 differentiable pruning method를 도입
• 논문 (INTERSPEECH 2023) : Paper Link

---

1. Introduction

• Text-to-Speech (TTS) 모델은 target speaker에 대한 충분한 training data를 사용하여 고품질의 음성을 합성할 수 있음
  • Target speaker의 limited data에 대한 Out-of-Domain (OOD) 합성의 경우, few-/zero-shot TTS 모델을 사용함
  • 특히 zero-shot TTS 모델은 target speaker에 대한 training data가 필요하지 않는다는 장점이 있음
    - 일반적으로 reference encoder를 사용하여 reference speech에서 style을 추출하는 방식을 사용함
    - BUT, zero-shot TTS 모델은 seen/unseen speaker 모두에 대해서 generalization 되어야 하므로 training과 추론 간의 domain mismatch 문제가 존재함
  • 이때 zero-shot TTS 모델의 합성 성능을 향상하기 위해서는, unseen speaker의 OOD data 뿐만 아니라 training data에 따른 다양한 generalization 능력이 필수적임
    - Training/test data 간의 high-degree mismatch가 있는 경우 overfitting을 방지하기 위해 더 많은 generalization이 필요하고, domain mismatch가 거의 없는 경우 overgeneralization이 발생할 수 있기 때문
    - 따라서 pruning 시 optimal generalization strength를 찾을 수 있어야 함

-> 그래서 zero-shot TTS 모델에 대한 OOD generalization을 위해 sparse attention pruning method를 제안함

 

• Self-Attention Pruning
  1. Self-attention layer에서 redundant connection을 제거하는 sparse attention mechanism을 TTS 모델에 적용
     • TTS 모델은 high-weight residual connection만을 사용하는 condition에서 training 되기 때문에 sparse attention mechanism을 통해 generalization ability를 크게 향상 가능
     • 특히 self-attention module에 sparsity를 반영하면 low-weight connection을 통한 backpropagation을 방지하기 때문에 TTS training에 사용되는 parameter 수가 reduce 되고 overfitting을 방지할 수 있음 
  2. Sparse attention에 대한 optimal pruning technique을 제안함
     • Attention weight가 pre-determined threshold 미만인 connection을 제거하는 vanilla pruning
     • Domain mismatch 정도에 대해 pruning strength를 adjust 하는 learnable threshold를 활용한 differentiable pruning method

 

< Overall of This Paper >

• TTS 모델의 핵심이 되는 transformer을 중심으로 self-attention module에 sparsity를 반영하여 connection을 pruning
• 추가적으로 generalization 정도를 control 할 수 있는 differentiable pruning technique을 도입
• 결과적으로 OOD zero-shot TTS에 대해 뛰어난 성능을 달성

2. Method

• 논문에서는 transformer-based zero-shot multi-speaker TTS 모델인 StyleSpeech를 baseline으로 pruning을 설계함
  • StyleSpeech architecture는 transformer-based phoneme encoder와 mel-spectrogram decoder, variance adaptor, reference encoder로 구성됨
  • Variance adaptor는 phoneme-level embedding에서 pitch, energy, duration을 예측하고, 예측된 duration을 사용하여 해당 embedding을 frame-level로 expand 함
  • Reference encoder는 input reference speech에서 speaker representation을 추출하고, Style-Adaptive Layer Normalization을 통해 encoder, decoder에 condition 함

Overview of StyleSpeech

- Sparse Attention

• Redundant connection을 pruning 하는 sparse attention은 deocoder에만 적용됨
  • 이는 다음의 이유 때문:
    1. Decoder의 frame-level sequence length $N$이 encoder의 phoneme-level sequence length보다 훨씬 길게 나타남
       - 즉, decoder가 encoder 보다 더 많은 수의 self-attention connection ($N\times N$)을 가지고 있음
    2. Encoder에 sparse attention을 적용하면 기존 self-attention module의 capacity가 감소하기 때문에 오히려 모델 성능이 저하됨
       
  • 결과적으로 논문에서는 decoder pruning을 위해 sparse mask를 정의하고, 이를 decoder self-attention module의 모든 attention head에 적용함
    - 이때 vanilla pruning, differentiable pruning 두 가지의 pruning 방식으로 나눌 수 있음
• Vanilla Pruning (VP)
  • Input sequence $\mathbf{x}$에 대해 2개의 linear transformation $W_{q}, W_{k}$를 통해 얻어진 query $Q$, key $k$가 주어진다고 하자:
    (Eq. 1) $Q=W_{q}\mathbf{x},\,\,K=W_{k}\mathbf{x}$
  • 그러면 multi-head self-attention layer의 $h$-th head의 attention probability $\mathcal{A}_{h}$는:
    (Eq. 2) $\mathcal{A}(i,j)=softmax\left(\frac{Q_{h}K_{h}^{T}}{\sqrt{d}}\right)_{(i,j)}$
    - $Q_{h}, K_{h}$ : 각각 $h$-th head의 query/key, $d$ : 해당 dimension
    - $\mathcal{A}_{h}(i,j)$ : $j$-th key에 해당하는 $i$-th query의 weight score
    
  • 다음으로 $h$-th head의 sparse mask matrix $SM^{h}$를 다음과 같이 정의할 수 있음:
    (Eq. 3) $SM^{h}_{(i,j)}=\left\{\begin{matrix}
    1 &  \mathrm{if}\,\, \mathcal{A}_{h}(i,j)\geq \mu_{i}\\
    0 &  \mathrm{if}\,\, \mathcal{A}_{h}(i,j)<\mu_{i}\\
    \end{matrix}\right.$
    (Eq. 4) $\mu_{i}=\frac{1}{N}\sum_{j=1}^{N}\mathcal{A}_{h}(i,j)$
    - $N$ : input sequence $\mathbf{x}$의 length
  • 결과적으로 $\mathcal{A}_{h}$에 적용된 $SM^{h}$ mask는 key axis를 따라 average attention weight $\mu_{i}$ 보다 작은 weight를 가지는 weak connection을 pruning 함
    1. 이때 실험적으로 head-axis를 따라 combine 된 common sparse mask를 사용하는 것이 $SM^{h}$를 각 head에 개별적으로 적용하는 것보다 성능이 우수한 것으로 나타남
    2. 즉, 다른 모든 head에 대한 각 head의 activated position을 고려하기 위해 adjusted sparse mask $SM_{OR}:=\bigcup_{h=1}^{H}SM^{h}$를 정의함
       - 여기서 $H$는 head의 개수이고 이를 모든 attention head에 동일하게 적용하고, $SM_{OR}$ mask는 training, inference 모두에서 사용됨

Overview of Differentiable Pruning

• Differentiable Pruning (DP)
  • Vanilla Pruning (VP)에서 $SM^{h}$의 threshold는 attention weight $\mu_{i}$의 평균으로 passively determine 됨
    - BUT, optimal threshold는 layer 수, generation task, domain mismatch degree 등에 따라 달라질 수 있으므로 threshold는 felxibly 하게 선택되어야 함
  • 따라서 논문에서는 learnable threshold를 사용하는 Differentiable Pruning (DP)를 제안함
    1. 먼저 learnabel threshold $\theta/N$를 inherit 하는 $h$-th head의 hard sparse mask $SM^{h}_{hard}$를 정의하면:
       (Eq. 5) ${SM^{h}_{hard}}_{(i,j)}=\left\{\begin{matrix}
       1 & \mathrm{if}\,\,\mathcal{A}_{h}(i,j)\geq \theta/N \\
       0 & \mathrm{if}\,\, \mathcal{A}_{h}(i,j)<\theta/N \\
       \end{matrix}\right.$
       - $\theta$ : trainable threshold parameter, $N$ : input length에 따라 threshold value를 adjust 하는 sequence length
       - 이때 binary mask $SM_{hard}^{h}$를 구하는 과정은 non-differentiable 하기 때문에 gradient descent를 통해서 $\theta$를 update 할 수 없음
    2. $\theta$의 update를 위해 Sigmoid function으로 정의된 differentiable soft sparse mask $SM^{h}_{soft}$를 도입함:
       (Eq. 6) $SM_{soft}^{h}=\sigma \left(\frac{\mathcal{A}_{h}-\theta/N}{T}\right)$
       - $T$ : $SM_{soft}^{h}$에서 $SM_{hard}^{h}$로 근사하기 위한 temperature ($=0.01$로 설정)
       - $SM_{soft}^{h}$의 값은 attention weight가 threshold $\theta$보다 큰 경우, 1에 가까움
  • 이를 기반으로 아래 [Algorithm1]의 two-phase training method를 적용함
    1. Phase 1에서 전체 모델은 soft sparse mask $SM_{soft}$를 사용하여 기존의 TTS loss term $\mathcal{L}_{tts}$로 training 되어 threshold $\theta$를 포함한 parameter를 update 함
       
       • 이때 pruning behavior를 보장하기 위해 regularization term $\mathcal{L}_{sp}$를 추가함:
         (Eq. 7) $\mathcal{L}_{sp}=\frac{1}{LH}\sum_{l=1}^{L}\sum_{h=1}^{H}\left(\overline{SM}_{soft}^{h}-R\right)^{2}$
         - $R$ : pruning strength를 indirectly determine 하는 hyperparameter, 0과 1 사이 값을 가지며 $R$ 값이 낮을수록 더 많은 connection을 제거함
         - $L$ : transformer layer 수, $H$ : 각 layer의 head 개수
       • Sparsity loss $\mathcal{L}_{sp}$는 모든 attention head와 decoder layer에 걸쳐 soft sparse mask $\overline{SM}_{soft}^{h}$와 $R$ 사이의 average $L2$-distance로 정의됨
         - 해당 loss term은 모델이 ODD data로 generalize 되도록 강제하고, 이를 사용하지 않으면 threshold $\theta$가 수렴되지 않음
         - 이는 $\mathcal{L}_{tts}$만 사용했을 때 in-domain data에 대해 $\theta$가 0으로 stuck 되어 connection이 pruning 되지 않은 경우, 모델이 가장 낮은 training loss를 얻기 때문
       • 요약하자면, Phase 1에서 $\theta$를 update 할 때 기존 tts loss term $\mathcal{L}_{tts}$와 regularization term $\mathcal{L}_{sp}$ 2가지 term을 사용함
         - $\mathcal{L}_{tts}$는 $\theta$를 0으로 줄이고, $\mathcal{L}_{sp}$는 OOD data에 대한 generalization을 위해 loss가 0이 되는 것을 방지함
       • 결과적으로 threshold는 서로 반대되는 두 loss에 의해 balance 되고, $\mathcal{L}_{tts}$를 충분히 최소화하는 범위 내에서만 self-attention connection을 pruning 함
         - 이때 sparsity ratio $R$을 변경하여 generalization 정도를 제어할 수 있음
    2. Phase 2에서 $\theta$를 제외한 모델 parameter는 Phase 1에서 threshold $\theta$가 학습한 hard sparse mask $SM_{hard}$를 사용하여 update 됨
       - 이때는 $\mathcal{L}_{sp}$를 사용하지 않고, fixed pruning strength를 사용하여 hard pruning condition에서 모델을 training 함
       - 최종적으로 Phase 2의 결과로 얻어진 모델을 inference에 사용함

Differentiable Pruning Algorithm

3. Experiments

- Settings

• Dataset : LibriTTS, VCTK
• Comparisons : StyleSpeech
  - VP : Vanilla Pruning
  - DP : Differentiable Pruning

- Results

• Evaluation on Zero-Shot TTS
  • VP를 적용한 모델은 CER을 제외한 모든 metric에서 baseline보다 뛰어난 성능을 발휘함
  • DP의 경우, 음질 측면에서 baseline, VP보다 뛰어난 성능을 보임
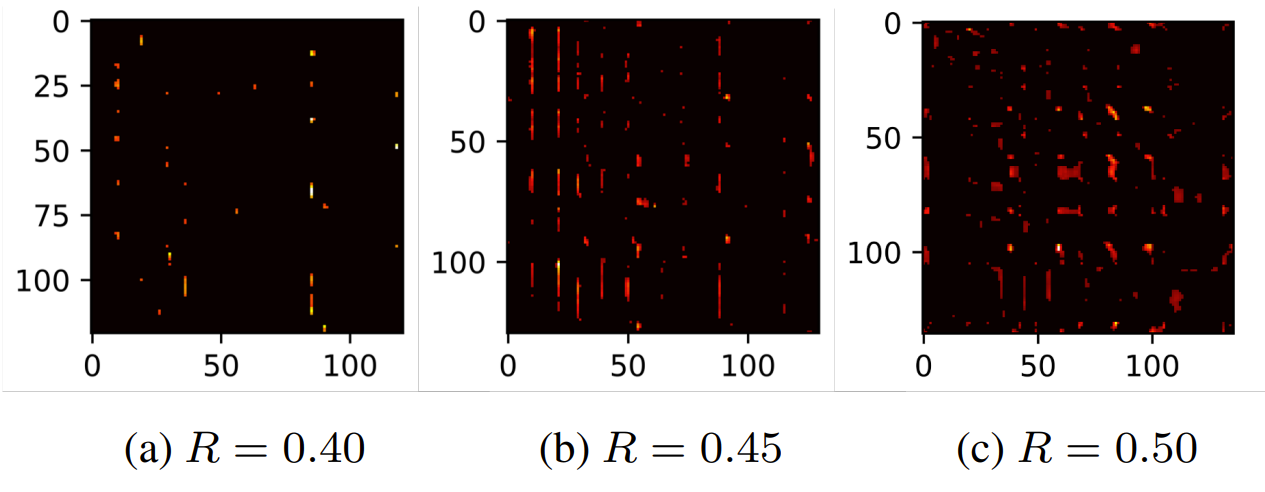
    - 이때 sparsity ratio $R$에 대해 과도한 pruning ($R : 0.45 \rightarrow 0.40$)을 적용한 경우, overgeneralization으로 인해 오히려 성능이 저하되는 것으로 나타남
  • 결과적으로 DP를 사용하면 zero-shot TTS의 성능을 크게 향상할 수 있음

Pruning 결과 비교

• Ablation Study
  • Hard mask $SM_{hard}$를 사용하지 않는 경우, 성능이 저하되는 것으로 나타남
    - Hard pruning은 text-to-mel conversion process에서 low-weight connection을 완전히 제외하여 모델의 generalization 성능을 향상할 수 있음
  • Regularization term $\mathcal{L}_{sp}$를 제거하는 경우에도 마찬가지로 성능 저하가 발생함
    - 이때 thresholds $\theta$가 initial value $0$에서 전혀 update 되지 않는 것으로 나타남

Ablation Study 결과

• Analysis of Differentiable Pruning
  • DP의 final threshold를 확인해 보면, $R$이 작을수록 threshold $\theta$가 커지므로 더 많은 connection이 pruning 됨
  • Pruned attention head를 확인해 보면, pruned TTS 모델은 몇 개의 self-attention connection 만을 사용하는 것으로 나타남
    - 이는 DP가 decoder의 in-domain data overfitting을 방지하고 generalization 성능을 향상한다는 것을 의미

Final DP Threshold

Pruned Attention Head