[Paper 리뷰] NAS-TasNet: Neural Architecture Search for Time-Domain Speech Separation

NAS-TasNet: Neural Architecture Search for Time-Domain Speech Separation

---

• Fully convolutional time-domain network인 Conv-TasNet은 speech separation에서 많이 사용되어 왔음
• Conv-TasNet의 성능을 극대화하기 위해 Neural Architecture Search를 도입할 수 있음
• NAS-TasNet
  • Conv-TasNet의 search space를 구축하기 위한 candidate operation의 정의
  • 최적의 separation module 구조를 결정하기 위한 gradient descent / reinforcement learning를 활용한 두 가지 search strategy 활용
  • 균형적인 parameter 업데이트를 위한 auxiliary loss 도입
• 논문 (IEEE Access 2022) : Paper Link

---

1. Introduction

• Real world에서 음성 작업은 주로 multi-speaker 환경에서 발생하므로 음성 처리 시스템은 distinct speaker의 음성을 구별할 수 있어야 함
  
  • 따라서 speech separation은 monaural speech를 constituent sound로 분리하는 것을 목표로 함
  • 기존의 speech separation은 time-frequecny domain에서 STFT를 사용하여 얻어지는 spectrogram을 활용했음
    - Spectrogram을 input으로 사용하여 각 source에 대한 spectrogram을 추정하는 방법
    - Mask를 추정한 다음, mixture representation과 곱해 각 source의 spectrogram에서 signal을 분리하는 방법
  • BUT, spectrogram 방식에는 두 가지 문제점이 존재
    1. Clean source phase에 대한 reconstruction이 까다로움
       - Phase 추정의 error로 인해 분리 성능이 제한됨
    2. 효과적인 분리를 위해서는 high-resolution frequency decomposition과 STFT를 위한 더 긴 temporal window가 필요함
       - High-resolution STFT는 latency를 늘려 실시간 활용을 어렵게 함
  • 따라서 time-frequency domain이 아닌 time-domain에서 직접적인 분리를 수행해야 함
• Conv-TasNet은 Temporal Convolutional Network (TCN)을 활용하는 time-domain mask estimation separation 모델임
  • Stacked dilated 1D CNN이 긴 receptive field를 커버함으로써 성능 향상을 달성했음
  • RNN, Transformer 등을 활용한 최신 모델들이 등장했지만, Conv-TasNet은 계산 복잡도 / latency 등의 측면에서 여전히 최신 모델들보다 우수함
• Neural Architecture Search (NAS)는 수동 설계의 한계를 극복하면서 최적의 성능과 효율성을 보장하는 모델을 탐색할 수 있는 방법임
  • 특히 speech separation을 위한 Conv-TasNet은 다양한 parameter로 구성되어 있음
    - 각 layer의 hyperparameter 조합에 따른 Conv-TasNet의 최적 성능에 대한 조사는 아직 이루어지지 않음
  • 결과적으로 NAS를 활용해 각 layer별로 최적의 hyperparameter 조합을 탐색한다면, Conv-TasNet의 성능과 효율성은 극대화될 수 있음

-> 그래서 Conv-TasNet을 기반으로 NAS를 적용하여 speech separation을 위한 최적의 모델인 NAS-TasNet을 탐색

 

• NAS-TasNet
  • Conv-TasNet에 NAS를 적용하기 위한 search space를 정의하는 candidate operation을 결정
  • NAS 적용 시 발생하는 architecture parameter 업데이트 불균형을 해결하기 위해 auxiliary loss를 활용
    - Long-term dependency를 capture 하고 모델의 학습 능력을 향상할 수 있음
  • Gradient / Reinforcement learning을 활용한 NAS를 통해 최적의 모델 구조를 탐색

< Overall of NAS-TasNet >

• NAS를 speech separation에 적용하는 최초의 시도
• Conv-TasNet에 적합한 search space 구성과 높은 GPU memory 사용을 극복하는 NAS 방법 제시
• Conv-TasNet에 대한 탐색 성능을 개선하는 auxiliary loss의 도입 

2. Search Space Configuration for Separation Network

• Single-channel speech separation은 mixture waveform $\mathbf{x} \in \mathbb{R}^{1 \times T}$에서 $N$개의 source $\mathbf{s}_{1}, ..., \mathbf{s}_{N} \in \mathbb{R}^{1 \times T}$에 대한 추정으로 정의될 수 있음:
  $\mathbf{x} = \sum^{N}_{i=1} \mathbf{s}_{i}$
• Conv-TasNet은 encoder, separator, decoder 3가지로 구성됨
  • Encoder $\mathcal{E}$는 input mixture signal $x$를 latent reperesentation $\mathbf{v}_{\mathbf{x}} = \mathcal{E}(\mathbf{x}) \in \mathbb{R}^{C_{\mathcal{E}} \times L}$로 변환
  • Separator $\mathcal{S}$는 $N$개의 source $\mathbf{s}_{1}, ..., \mathbf{s}_{N} \in \mathbb{R}^{T}$ 각각에 대해 대응하는 mask $\hat{\mathbf{m}_{i}} \in \mathbb{R}^{C_{\mathcal{E}} \times L}$을 추정
    - Latent space $\hat{\mathbf{v}_{i}}$에 대한 추정 latent representation은, element-wise 추정 mask $\hat{\mathbf{m}_{i}}$와 encoded mixture representation $\mathbf{v}_{\mathbf{x}}$를 곱해서 얻어짐
  • Decoder $\mathcal{D}$는 latent space vector $\hat{\mathbf{s}_{i}} = \mathcal{D}(\hat{\mathbf{v}_{i}})$로 부터 target source를 추정
    - 각 1D CNN block은 dilation factor $d$가 exponential 하게 증가하도록 구성하여 모델이 큰 receptive field를 가지도록 함
    - 결과적으로 dilated network는 input의 long-term dependency를 처리할 수 있는 충분한 temporal context window를 가지게 됨
  • Separation model은 $R$번 repeat 하는 $X$개의 convolutional block stack으로 구성
    - 여기서 일반 Conv-TasNet 대신 아래의 개선된 TDCN++를 사용
    1. 모든 feature와 frame에 대한 globla layer noramlization이 frame에 대한 feature-wise layer normalization으로 대체
    2. Longer-range skip-residual connection의 사용
    3. Learnable scaling parameter를 도입

Conv-TasNet architecture

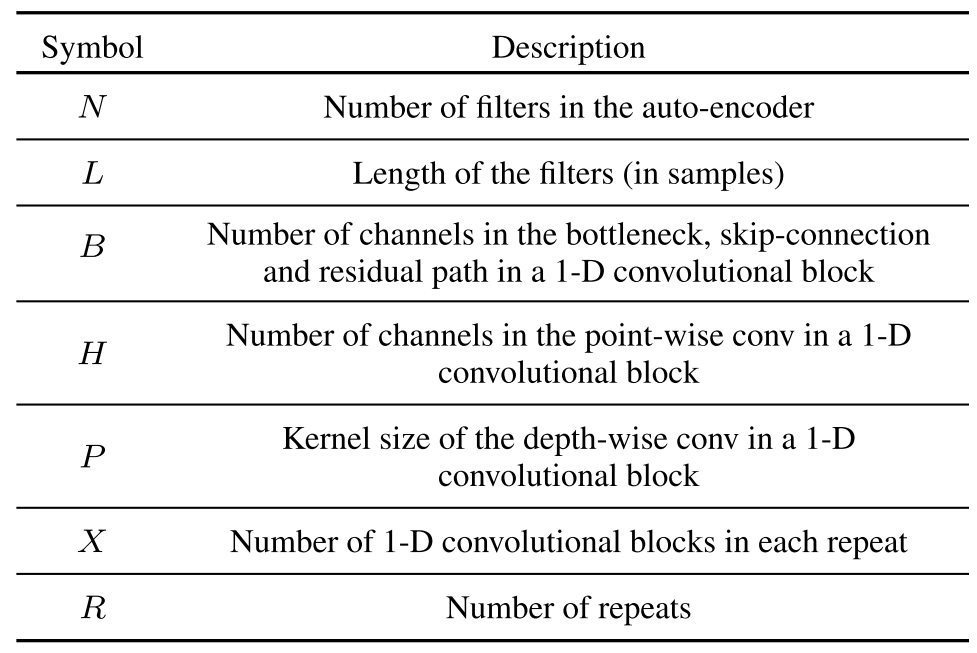
• Conv-TasNet의 hyeperparameter 중 $N$과 $L$을 제외한 모든 hyperparameter는 separation module과 관련되어 있음
  • AutoEncoder variable ($N, L$)도 성능 최적화에 중요한 요소이지만 복잡도가 증가함
    - 따라서, 본 논문에서는 NAS를 1D convolutional block 기반 separation module에만 적용
  • 결과적으로 separation module의 $H, P, X, R$에 대한 최적 조합을 결정하기 위한 NAS를 설계해야 함

최적화를 위한 주요 hyperparameter

• Search space는 2가지 종류가 존재
  1. Network-based search space
     - 전체 network를 탐색하는 방식
  2. Cell-based search space
     - Cell 별로 NAS를 수행하고 cell structure를 repeating 하여 network를 구성하는 방식
     -> 본 논문에서는 network-based search space를 활용함
• NAS-TasNet의 search space는 kernel size $P$와 expansion ratio $H$에 대해 구성됨
  • Kernel size $\{3, 5 \}$와 expansion ratio $\{ \times 1, \times 2, \times 4 \}$를 가지는 1D convolution block 집합을 활용
  • Layer와 repeat count ($X, R$)에 대한 search space를 설계하기 위해, zero layer를 추가
    - Zero layer는 input과 동일한 차원의 zero tensor를 출력
    - 모든 1D convolution block은 skip connection을 포함하고 있기 때문에, block 사이에 zero layer를 추가하는 것은 block 하나를 생략하는 것과 동일한 효과를 가짐
  • Repeat에서 layer 수를 조정하면 exponential dilation pattern이 깨질 수 있음
    - Zero layer를 제외한 하나의 repeat layer의 index를 재할당하여 1D convolution block의 dilation을 조정
  • Mixed operation은 7개의 candidate operation으로 구성:
    2개의 kernel size, 3개의 convolution channel, 1개의 zero layer
  • NAS hyperparameter $B, R_{max}, X_{max}$의 설정
    - $B$ : separator $\mathcal{S}$의 bottelneck size (128)
    - $X_{max}$ : 각 repeat에서 1D convolution block의 최대 개수 (8)
    - $R_{max}$ : 3, 4 두 가지 값으로 실험

Search space 구성을 위한 candidate operation

3. Architecture Search Strategy

• 앞서 정의된 network-based search space를 기반으로 architecture search를 수행

- Differentiable Architecture Search

• DARTS는 candidate operation의 discrete set에 대한 relaxtion을 제시
  • 가능한 모든 operation에 대해 특정 operation의 categorical choice를 softmax로 relax 함
    - Relaxtion은 search space를 continuous 하게 만들기 때문에 gradient descent를 활용한 architecture 최적화가 가능하게 만듦
  • DARTS를 수행하기 위해,
    - 모든 candidate operation과 architecture parameter $\alpha$를 포함하는 mixed operation으로 over-parameterize 된 network (mixed operation network)를 구성
    - 이때 Architecture를 Directed Acyclic Graph (DAG)로 표현하면, mixed operation network를 DAG의 특정 edge $e_{i}$를 활용하여 $\mathcal{N} (e, ..., e_{n})$으로 나타낼 수 있음
  • Search space의 모든 architecture를 포함하는 mixed operation network를 구성하기 위해,
    - 각 edge를 mixed operation $m_{\mathcal{O}}$로 설정
    - $\mathcal{O} = \{ o_{i} \}$ : Candidate primitive operation, $\mathcal{N}(e = m^{1}_{\mathcal{O}}, ..., e_{n} = m^{n}_{\mathcal{O}})$ : network
• DARTS에서 mixed operation과 input이 각각 $m_{\mathcal{O}}, x$로 정의된 경우, $m_{\mathcal{O}}(x)$는 $\{ o_{i}(x) \}$의 weighted sum과 같음
  • 이때 weight는 $N$개의 실수값 architecture parameter $\alpha_{i}$에 softmax를 적용하여 계산됨:
    $m_{\mathcal{O}}(x) = \sum^{N}_{i=1} p_{i}o_{i}(x) = \sum^{N}_{i=1} \frac{exp(\alpha_{i})} {\sum_{j} exp(\alpha_{j})} o_{i}(x)$
    - Architecture parameter $\alpha_{i}$는 softmax를 사용하여 mixed operation에서 해당하는 candidate operation의 확률을 결정
  • Over-parameterized network를 통해 DARTS는 model parameter $w$와 architecture parameter $\alpha$를 업데이트하여 architecture의 objective function을 최적화하는 bi-level optimization을 수행
    - 학습이 진행됨에 따라 성능을 향상하는 operation의 $\alpha_{i}$가 증가하고 나머지는 감소됨
    - 학습 완료 시, $\alpha$ 값이 가장 큰 operation을 제외한 나머지를 모두 pruning 하여 최적화된 architecture를 결정

DARTS의 동작 과정

- Architecture Search with GPU Memory Saving

• DARTS는 모든 $N$개 path에 대한 output feature map이 계산되어 저장되어 많은 양의 GPU memory가 필요함
  • Time-domain speech separation 작업의 경우, input이 대용량의 raw audio data이기 때문에 DARTS의 weighted sum 계산 시 memory 부족 문제가 발생함
  • 따라서, memory를 효과적으로 활용할 수 있는 ProxylessNAS를 활용하여 DARTS를 수행
    - Binarization을 통해 over-parameterized mixed operation network에서 하나의 path만 유지하도록 함
    - 이때, $N$개 실수 path weight $\{ \alpha_{i} \}$를 아래의 binary gate를 통하여 binarization: 
    $g = binarize (p_{1}, ..., p_{N}) = \left \{ \begin{matrix} [1,0, ..., 0] \\ ... \\ [0,0, ..., 1] \end{matrix} \right.$
    - Binary gate $g$를 적용한 mixed operation의 output은:
    $m^{Binary}_{\mathcal{O}}(x) = \sum^{N}_{i=1} g_{i} o_{i}(x) = \left \{ \begin{matrix} o_{1}(x) \\ ... \\ o_{N}(x) \end{matrix} \right.$
  • Binary gate를 사용한 mixed operation은 runtime 시 memory에서 하나의 path만 activate 됨
    - 결과적으로 over-parameterized network를 학습하는데 필요한 memory 요구사항이 줄어듦
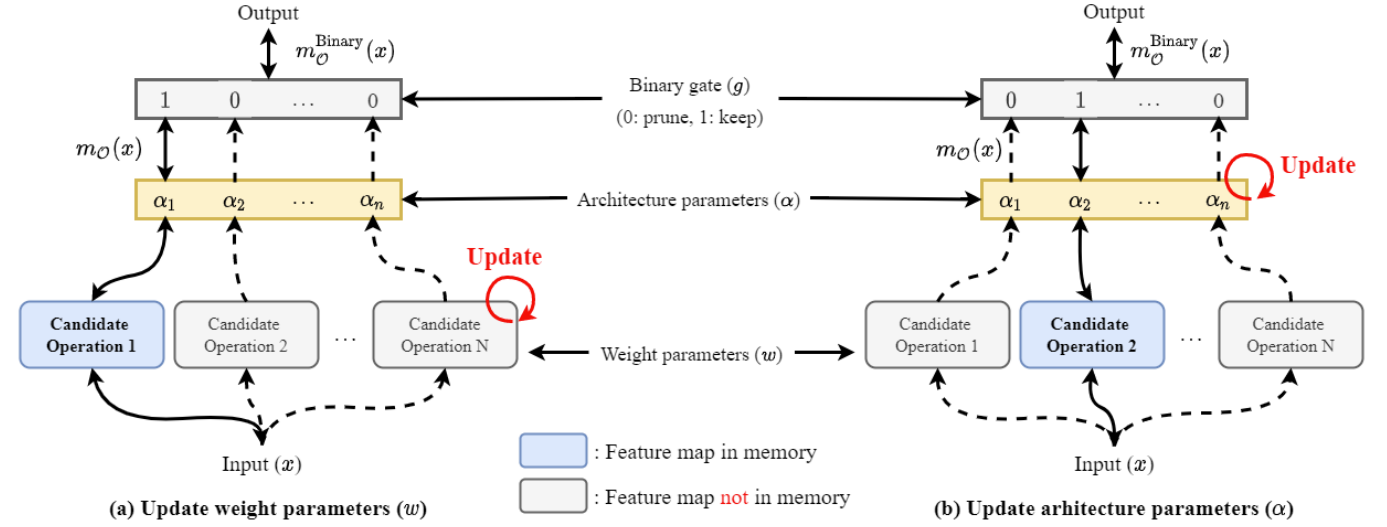
• Mixed operation network에서 binarized architecture parameter에 대한 학습 과정은
  • Network weight parameter 학습
    1. Architecture parameter $\alpha$를 freeze 하고 input data의 각 batch에 대해 binary gate를 stochastic sampling 함
    2. Active path에 대한 weight parameter는 training set의 gradient descent를 통해 업데이트됨
  • Architecture parameter $\alpha$ 학습
    1. Weight parameter $w$가 freeze 되고 binary gate를 reset 함
    2. Architecture parameter는 validation split을 통해 업데이트됨
  • Weight parameter $w$와 달리 architecture parameter $\alpha$는 mixed operation 계산에 포함되지 않으므로 일반적인 gradient descent를 통해 업데이트할 수 없음
    - 이때, 계산 그래프에 포함된 binary gate $g$는 $\partial m^{Binary}_{\mathcal{O}}(x)/\partial g$와 같이 backpropagation을 통해 계산될 수 있음
    - 하지만 $\partial m^{Binary}_{\mathcal{O}} (x) / \partial g$를 계산하기 위해서는, mixed operation $m^{Binary}_{\mathcal{O}}(x)$의 ouptut을 계산하고 저장해야 함
    -> 결과적으로 architecture parameter 업데이트를 위해서는 기존보다 $N$배의 GPU memory를 요구함
  • GPU memory 문제를 해결하기 위해,
    - $N$개의 candidate 중에서 하나의 path를 선택하는 작업은 여러 개의 binary selection operation으로 factorize 함
    - 이때 Multinomial 분포 ($p_{1},..., p_{N}$)를 기반으로 두 개의 path를 sampling 하고 다른 모든 path를 mask 함
    -> 따라서 candiate 수가 일시적으로 $N$에서 2로 감소하게 되므로, 두 sampling path에 대한 architecture parameter를 업데이트할 수 있음
  • 최종적으로 architecture parameter에 대한 학습이 완료되면, 중복 path를 제거하여 compact architecture를 얻음

ProxylessNAS의 동작 과정

- Model Size-aware Objective Function

• Separation 작업은 scale-invariant source-to-distortion ratio (SI-SDR)을 최대화하는 것을 목표로 함
  • 따라서 objective function으로써 negative permutation-invariant SI-SDR이 사용됨
  • 이때 loss function $\mathcal{L}_{-SI-SDR}$은 추정값 $\hat{\mathbf{s}}$와 target clean source $t$에 대해 정의됨:
    $\mathcal{L}_{-SI-SDR} = - SI-SDR(\mathbf{t}^{*}, \hat{\mathbf{s}}) = -10 log_{10} \left ( \frac { || \alpha \mathbf{t}^{*} ||^{2}} {|| \alpha \mathbf{t}^{*} - \hat{\mathbf{s}}||^{2}} \right )$
    - $\mathbf{t}^{*}$ : SI-SDR을 최대화하는 source의 permutation
    - $\alpha = \hat{\mathbf{s}}^{T} \mathbf{t}^{*} / || t ||^{2}$ : scalar 값

• SI-SDR 외에 architecture searh 과정에서 더 적은 parameter를 가지도록 모델 size를 최적화할 수 있음
  • Floating-point operations (FLOPs)를 활용하여 효율적인 architecture를 탐색할 수 있음
    - BUT, FLOPs는 non-differentiable 하므로 ProxylessNAS에서 제안된 FLOPs에 대한 loss function term이 반영된 architecture search objective function을 사용
  • 각 $o_{j}$ $o_{j}$를 선택할 확률을 나타내는 path weight $p_{j}$와 연관되어 있는 candidate set $\{ o_{j} \}$에 대한 mixed operation이 있다고 할 때, mixed operation의 expected FLOPs는:
    $\mathbb{E} [FLOPs_{i}] = \sum_{j} p^{i}_{j} \times F(o_{j}^{i})$
    - $\mathbb{E} [FLOPs_{i}] = $i$th mixed operation의 expected FLOPs
    - $F(\cdot)$ : predicton function
    - $F(o^{i}_{j})$: $o^{i}_{j}$의 predicted latency
  • 위를 통해 추정된 FLOPs는 architecture parameter에 따라 미분가능함
    - 이때, $\mathbb{E}[FLOPs_{i}]$의 gradient는 $\partial \mathbb{E}[FLOPs_{i}]/\partial p^{i}_{j} = F(o^{i}_{j})$
    - 전체 network에 대한 expected FLOPs는 mixed operation들의 expected FLOPs의 합과 같음:
    $\mathbb{E}[FLOPs] = \sum_{i} \mathbb{E} [FLOPs_{i}]$
  • 따라서, network의 expected latency는 scaling factor $\lambda_{2} (>0)$을 곱하여 negative SI-SDR loss에 더해지고, 이때 최종 loss function은:
    $\mathcal{L} = \mathcal{L}_{-SI-SDR} + \lambda_{1} || w ||^{2}_{2} + \lambda_{2} \mathbb{E} [FLOPs]$
    - $\lambda_{1} || w ||^{2}_{2}$ : weight decay term

- Reinforce-based Approach

• Gradient 방식 외에 Reinforcement learning을 활용하여 architecture search를 수행할 수 있음
  • 이때 binarized parameter를 업데이트하는 objective는 reward $R(\cdot)$을 최대화하는 최적의 binary gate를 결정하는 것으로 볼 수 있음
  • 따라서, accuracy term을 SI-SDR로 변경하고, latency를 FLOPs로 변경한 reward는:
    $R(\mathcal{N}_{g}) = SI-SDR (\mathcal{N}_{g}) \times \left [ \frac{FLOPs(\mathcal{N}_{g})} {T_{ref}} \right ]^{w}$
    - $\mathcal{N}_{g}$ : sampling 된 binary gate가 있는 현재 sampling network
    - $T_{ref}$ : network의 reference target FLOPs로, hard constraint로 사용
    - $w$ : SI-SDR과 FLOPs 간의 trade-off를 조절하는 weight factor
  • 결과적으로 reward function은 hard constraint하에서 SI-SDR을 최대화함
• Reinforcement 기반 NAS는 mixed operation network에서 binarized parameter에 대해 아래의 업데이트를 수행함:
  $J(\alpha) = \mathbb{E}_{g \sim \alpha} [ R(\mathcal{N}_{g})] = \sum_{i} p_{i} R(\mathcal{N}(e=o_{i}))$
  $\nabla_{\alpha}J(\alpha) = \sum_{i} R(\mathcal{N}(e=o_{i})) \nabla_{\alpha}p_{i}$
  $\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =\sum_{i} R(\mathcal{N}(e=o_{i}))p_{i} \nabla_{\alpha} log (p_{i})$
  $ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \mathbb{E}_{g \sim \alpha} [R(\mathcal{N}_{g}) \nabla_{\alpha} log (p(g))] $
  $ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \approx \frac{1}{M} \sum_{i=1}^{M} R(\mathcal{N}_{g^{i}}) \nabla_{\alpha} log (p(g^{i}))$
  - $g^{i}$ : $i$th sampled binary gate
  - $p(g^{i})$ : sampling probability (policy)
  - $\mathcal{N}_{g^{i}}$ : binary gate $g^{i}$를 기반으로 하는 compact network
  - $M$ : reinforcement NAS의 hyperparameter, 하나의 mini-batch에서 sampling 된 architecture 수를 의미

4. Auxiliary Loss

• NAS 수행 중 mixed operation 간의 architecture parameter 업데이트 불균형 문제를 완화하고, 모델의 분리 성능을 향상하기 위해 auxiliary loss를 도입
  • Gradient-based search 시 architecture parameter는 각 mixed operation에 할당됨
    - 이때, mixed operation의 output은 candidate operation output의 weighted sum
    - Weight는 architecture parameter에 softmax를 적용한 값
  • NAS가 진행됨에 따라 architecture parameter를 업데이트하면서 weight가 수정되고, candidate operation 중 가장 적합한 operation의 weight가 증가함
    - 각 mixed operation의 weight는 특정한 candidate operation에 대한 confidence level이 될 수 있고, weight가 증가할수록 weight 분포의 entropy는 감소함
  • 이때, entropy는 확률 분포의 무작위성을 의미하고, 이산형 확률 분포의 entropy는:
    $H = - \sum^{N}_{i=1} p_{i} ln(p_{i})$
    -$H$ : 확률 분포의 entropy, $N$ : candidate operation 수
    - $p_{i}$ : mixed operation에서 해당 candidate operation의 확률로, DARTS의 mixed operation에 대한 weight의 weighted sum
  • NAS epoch에 대한 mixed operation의 각 weight 분포의 entropy 감소를 확인해 보면,
    - 앞쪽에 위치한 mixed operation의 entropy는 거의 감소하지 않는 반면, 마지막에 위치한 operation의 entropy는 급격하게 감소함
    - Mixed operation의 위치에 따라 architecture parameter 업데이트가 다르다는 것을 의미
  • 이는 separation module의 깊이에 따라 gradient가 비효율적으로 backpropagate 되기 때문에 전면부의 layer는 discriminative feature를 제공할 수 없기 때문
    - 결과적으로 초반의 mixed operation는 discriminating feature의 부재로 candidates 간의 perference를 결정할 수 없기 때문에, 무작위로 선택되는 것임
• Auxiliary loss는 서로 다른 위치를 가지는 mixed operation들 간의 parameter 업데이트 불균형을 해결할 수 있음
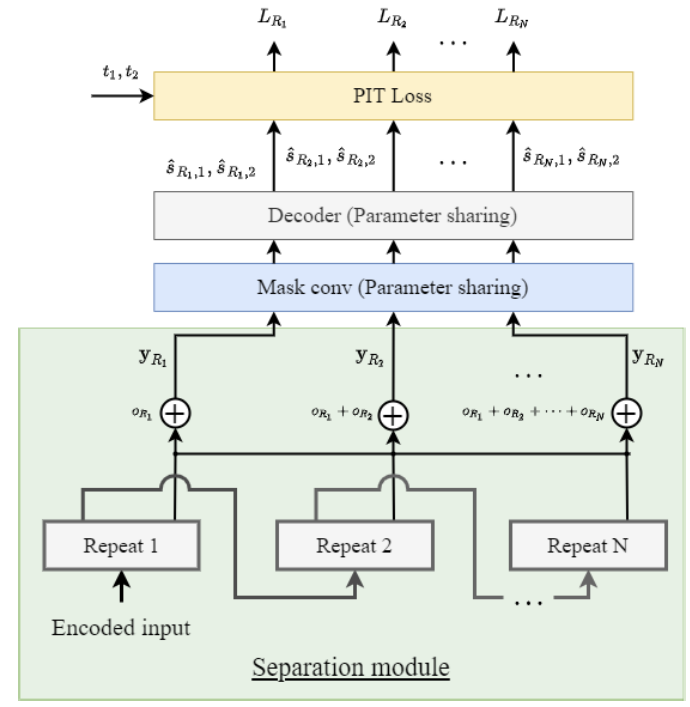
  • 각 repeat 별 layer의 skip connection output에 대한 element-wise sum을 $y_{R_{n}}$이라고 하고, 각 repeat 별 loss를 $L_{R_{n}}$이라 하자.
    - $L_{R_{n}}$을 사용하면 추가적인 모델을 사용하지 않고 기존 mask network와 decoder를 재사용하여 repeat 개수만큼 loss를 계산할 수 있음
    - 이때 초기의 1D CNN block repeat에 대한 mask 추정이 이후의 repeat loss 보다 더 높다고 가정하기 때문에, 초기 repeat의 영향을 제어하기 위해 weighted sum을 활용
    - Weighting pattern을 유지할 수 있는 moving average를 적용
  • 따라서, auxiliary loss $L_{aux}$는:
    $L_{aux} = L_{R_{t}} = \left \{ \begin{matrix} L_{R_{t}}, \, t=1 \\ \alpha L_{R_{t}} + (1-\alpha)L_{R_{t-1}}, \, t>1  \end{matrix} \right.$
    - $\alpha$ : 0과 1 사이의 smoothing constant로 weight 감소 정도를 나타냄
    - $\alpha$가 크면 earlier repeat decay로 인한 loss가 빨라짐

Conv-TasNet에 대한 auxiliary loss 획득 과정

5. Experiments

- Settings

• Dataset : WSJ0-2mix, WSJ0-3mix
• Comparisons : Conv-TasNet, TDCN++

- Experimental Results of Architecture Search

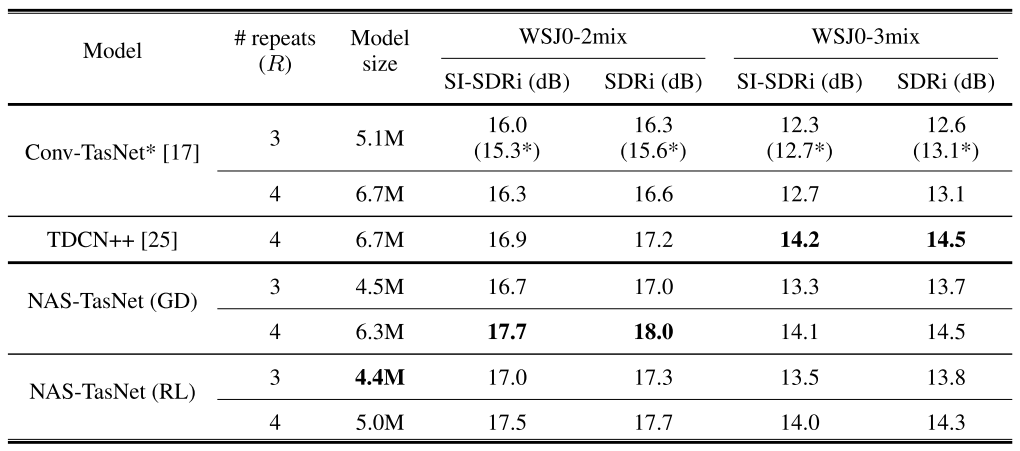
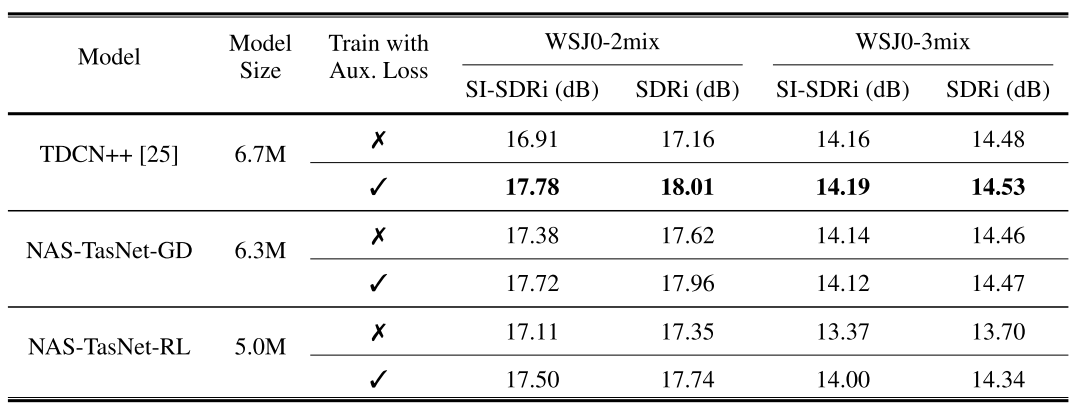
• Reinforcement learning을 통해 탐색된 모델은 크기가 2M 더 작은데도 불구하고 WSJ0-2mix에서 더 좋은 성능을 보임
  • 탐색된 모델에 대한 WSJ0-3mix에 대한 일반화를 비교한 결과, NAS-TasNet은 backbone과 유사한 성능을 보임
    - 탐색된 모델이 WSJ0-2mix에 대해 overfitting 되지 않았다는 것을 의미
  • NAS를 위해 4개의 RTX 2080 Ti GPU에 대해 2일이 소모됨 (추정 효율성은 8 GPU days)

성능 비교 결과

• NAS를 통해 얻어진 compact separation module을 확인해 보면,
  • NAS-TasNet-GD의 경우 zero layer를 활용하여 모델 크기를 조정
  • NAS-TasNet-RL의 경우 zero layer를 사용하지 않고 layer의 channel expansion ratio를 제어하여 모델 크기를 조정
  • 많은 수의 parameter를 가진 candidate operation이 각 반복에서 front layer로 선호됨

NAS를 통해 탐색된 model 구조들

- Auxiliary Loss Effect

• Auxiliary loss는 mixture operation 간의 parameter 업데이트 불균형을 해소하고, layer들이 무작위로 선택되는 것을 방지함
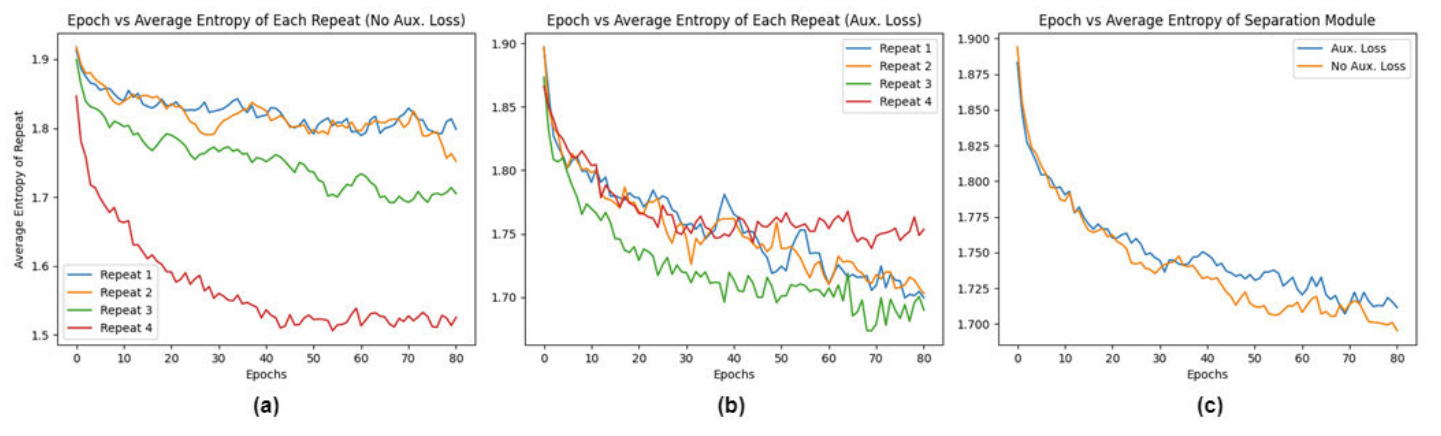
• Auxiliary loss의 효과를 조사하기 위해 auxiliary loss의 여부에 따른 repeated mixed operation에 대한 평균 entropy 감소를 비교
  • (a) Auxiliary loss가 적용되지 않은 경우
    - 가장 큰 entropy 감소는 network 마지막에 위치한 repeat 4에서 관찰되었고, network 전면부에 위치한 repeat 1, 2는 entropy 감소가 적었음
    - 결과적으로 network 전면부에 대한 operation을 빠르게 수렴되어 다양한 operation을 시도하지 못해 거의 무작위로 선정됨
  • (b) Auxiliary loss가 적용된 경우
    - 모든 repeat에 대해 평균 entropy는 비슷한 수준으로 감소
    - 전체 network에 대해 parameter 업데이트가 균형을 이루었다는 것을 의미
  • (c) 전체 separation module에 대한 평균 entropy를 비교
    - Auxiliary loss 사용 여부와 무관하게 전체 separation module에 대한 entropy 감소는 비슷하게 나타남
    - 결과적으로 auxiliary loss는 mixed operation 간의 entropy 편차를 줄인다고 볼 수 있음

Auxiliary loss 여부에 대한 entropy 비교

• Auxiliary loss 사용에 대한 spearaion accuracy 향상 여부를 비교해 보면,
  • Auxiliary loss를 사용했을 때, WSJ0-2mix, WSJ0-3mix 모두에서 성능 향상이 관찰됨
  • 탐색된 NAS-TasNet에 대해서도 auxiliary loss가 적용되었을 때, 더 나은 성능을 보임

Auxiliary loss 적용에 따른 성능 비교 결과