[Paper 리뷰] On Loss Functions and Evaluation Metrics For Music Source Separation

On Loss Functions and Evaluation Metrics For Music Source Separation

---

• Music source separation을 위해 어떤 loss function이 효과적인 분리를 제공하는지 조사
• 대표적인 Audio source separation loss들을 포함한 벤치마킹 평가
• Signal-to-Distortion ratio를 대체할 수 있는 평가 지표를 조사
• 논문 (ICASSP 2022) : Paper Link

---

1. Introduction

• Music source separation은 혼합된 오디오 신호에서 원래 신호를 복구하는 것을 목표로 함
  
  • 대부분의 Music source separation은 time-frequency domain에서 동작하는 회귀모델을 활용
    - Source의 magnitude spectrogram을 추정하거나 separation mask를 추정하는 방식
  • Spectrogram-based model은 time-domain으로 돌아가기 위한 phase를 무시하는 경우가 많음
    - Mixture의 phase를 활용할 수 있지만 error를 발생시킬 수 있음
    - 학습 단계에서 phase error를 캡처하기 위해 phase-sensitive time-domain loss를 사용할 수 있음
  • Scale-invariant time-domain loss는 source separation에서 대중적으로 사용되는 방식
    - Spectrogram 신호에 대한 scale-invariant 회귀 loss를 고려할 수 있음
  • L1, L2 loss는 각각 uni-modal로 가정되는 출력 분포의 중앙값과 평균을 예측할 수 있음
    - 실제 분포가 가정된 분포와 다르면 예측이 제대로 이뤄지지 않을 수 있음
    - Adversarial loss나 Deep feature loss 같은 regularizer를 고려 가능

-> 그래서 Music source separation에서 어떤 loss의 사용이 최적의 분리를 제공할 수 있는지를 조사

 

< Overall of this paper >

• 대표적인 Audio source separation loss에 대한 조사 및 벤치마킹 평가
• Loss와 인간 판단 간의 연관성 파악을 위한 주관적 평가

논문에서 고려된 Source Separation Loss들

2. Audio Source Separation Losses

- Time Domain Losses

• $\mathcal{T}$개 sample의 audio $x_{t}$가 주어지면, $K$개의 서로 다른 source $\tilde{y}_{t,k}$를 추출
  • 일반적인 회귀 Loss (L1, L2 loss)
    - $L1_{tme} = \frac{1}{\mathcal{T} K} \sum_{t,k} | \tilde{y}_{t,k} -  y_{t,k} |$ 
    - $L2_{time} = \frac{1}{\mathcal{T} K} \sum_{t,k} | \tilde{y}_{t,k} - y_{t,k} |^{2}$
  • Signal-to-Distortion ratio (SDR), Scale-Invariant SDR (SISDR)은 training, evaluation 과정에서 자주 사용됨
    - $ SISDR_{time} = \frac{-10}{\mathcal{T} K} \sum_{t,k} log_{10} \begin{pmatrix} \left | \frac{\tilde{y}^{T}_{t,k} y_{t,k}} {|y_{t,k}|^{2}} y_{t,k} \right |^{2} \\ \hline \left | \frac{\tilde{y}^{T}_{t,k} y_{t,k}} {|y_{t,k}|^{2}} y_{t,k} - \tilde{y}_{t,k} \right |^{2} \end{pmatrix} $
  • 일부 케이스에서는 scale-invariant 가정이 성립하기 어려우므로, Scale-dependent SDR (SDSDR)이 더 선호될 수 있음
    - $SNR = \frac{10}{\mathcal{T} K} \sum_{t,k} log_{10} ( \frac{|y_{t,k}|^{2}} {|\tilde{y}_{t,k} - y_{t,k}|^{2}} )$
    - $L_{down} = SNR + \frac{10} {\mathcal{T} K} \sum_{t, k} log_{10} ( ( \frac {\tilde{y}^{T}_{t,k}y_{t,k}} {|y_{t,k}|^{2}} ) ^{2} )$
    - $SDSDR_{time} = -min(SNR, L_{down})$
  • SISDR과 동치인 log-compressed L2 loss를 사용할 수 있고, 추가적으로 L1 loss의 변형도 함께 고려
    - $LOGL2_{time} = \frac{10} {\mathcal{T} K} \sum_{k} log_{10} \sum_{t} |\tilde{y}_{t,k} - y_{t,k}|^{2}$
    - $LOGL1_{time} = \frac{10} {\mathcal{T} K} \sum_{k} log_{10} \sum_{t} |\tilde{y}_{t,k} - y_{t,k}|$

- Spectrogram-based Losses

• 대부분의 source separation model은 source $k$ 별로 magnitude spectrogram $|\tilde{Y}_{n,w,k}|$를 추정
  • $STFT(x_{t}) = X_{n,w}$ : Short-Time Fourier Transform
    - $n$ : $N$개의 전체 frame의 frame index
    - $w$ : $\Omega$개의 frequency bin의 index 
  • L1, L2 와 같은 일반적인 회귀 loss
    - $L1_{freq} = \frac{1}{N \Omega K} \sum_{n,w,k} \left | |\tilde{Y}_{n,w,k}| - |Y_{n,w,k}| \right |$
    - $L2_{freq} = \frac{1}{N \Omega K} \sum_{n,w,k} \left | |\tilde{Y}_{n,w,k}| - |Y_{n,w,k}| \right |^{2}$
• $|\tilde{Y}_{n,w,k}|$는 phase information을 포함하지 않음
  • $|\tilde{Y}_{n,w,k}|$에 time-domain 신호를 합성하려면 Inverse STFT (ISTFT)를 통한 phase information이 필요
    - $\tilde{y}_{t,k} = ISTFT(|\tilde{Y}_{n,w,k}| \angle X_{n,w})$
    - 입력 mixture의 noisy phase로써 $\angle X_{n,w}$를 주로 사용하지만 error를 발생시킬 수 있음
  • Phase Sensitive Target $Y^{PSA}_{n,w,k}$를 사용해 noisy phase의 영향을 완화
    - $Y^{PSA}_{n,w,k} = |Y_{n,w,k}| cos(\angle X_{n,w} - \angle Y_{n,w,k})$
    - $L_{PSA} = \frac{1}{N \Omega K} \sum_{n,w,k} \left | |\tilde{Y}_{n,w,k}| - Y^{PSA}_{n,w,k} \right |^{2}$
• Mask-based model은 spectrogram 신호와 함께 사용됨
  
  • Ratio mask는 mixture $X_{n,w}$에서 source를 필터링함
    - $M_{n,w,k} = \frac{|Y_{n,w,k}|} {\sum_{k} |Y_{n,w,k}|}$
    - $|Y_{n,w,k}| = M_{n,w,k} \bigodot |X_{n,w}|$
  • Mask-based model loss
    - $L1_{mask} = \frac{1}{N \Omega K} \sum_{n,w,k} | \tilde{M}_{n,w,k} - M_{n,w,k}|$
    - $L2_{mask} = \frac{1}{N \Omega K} \sum_{n,w,k} | \tilde{M}_{n,w,k} - M_{n,w,k}|^{2}$
• Source separation model은 다른 source로 부터 간섭을 받기 쉬움
  
  • Dissimilarity loss는 각 source에 대한 L2 항을 추가하여 다른 source의 간섭을 완화
    - $L_{dissim} = \frac{1}{N \Omega K} \sum_{n,w,k} ( \left | |\tilde{Y}_{n,w,k}| - |Y_{n,w,k}| \right |^{2} - \beta \sum_{\tilde{k}} \left | |\tilde{Y}_{n,w,k}| - |Y_{n,w, \tilde{k} \neq k}| \right |^{2})$
• $SISDR_{time}$를 spectrogram에 적용하면 $Y_{n,k,w}$와 $\tilde{Y}_{n,k,w}$를 각각 $Y_{nw,k}$와 $\tilde{Y}_{nw,k}$로 reshape 시킴
  • 이때 $LOGL1_{freq}$, $LOGL2_{freq}$을 spectrogram에 적용 가능
    - $LOGL1_{freq} = \frac{10}{N \Omega K} \sum_{k} log_{10} \sum_{n,w} \left | |\tilde{Y}_{n,w,k}| - |Y_{n,w,k}| \right |$
    - $LOGL1_{freq} = \frac{10}{N \Omega K} \sum_{k} log_{10} \sum_{n,w} \left | |\tilde{Y}_{n,w,k}| - |Y_{n,w,k}| \right |^{2}$
• Log magnitude $L_{mag}$와 spectral convergence $L_{sc}$로 구현된 Multi-resolution STFT loss $L_{MRS}$
  • 다양한 FFT size, window, overlap을 가지는 single-resolution STFT로 구성됨
    - $L_{sc} = \frac{1}{K} \sum_{k} \frac{\sqrt{\sum_{n,w} (|\tilde{Y}_{n,w,k}| - |Y_{n,w,k})^{2} }} {\sqrt{\sum_{n,w} |Y_{n,w,k}|^{2} }}$
    - $L_{mag} = \frac{1}{K} \sum_{n,w,k} (log_{10} | \tilde{Y}_{n,w,k}| - log_{10} |Y_{n,w,k}|)$
    - $L_{MRS} = \frac{1}{O} \sum_{o} (L^{(o)}_{sc} + L^{(o)}_{mag})$
    

- Adversarial Loss

• Adversarial loss를 위해 label smoothing과 함께 least-square의 변형을 적용
  • Separation을 위한 adversarial 구성
    1. Paired $X$와 unpaired $\hat{X}$로 이루어진 mixture에서 그럴듯한 separated magnitude spectrogram인 $\tilde{Y}$를 생성하는 separator $f$
    2. Separator에 의해 생성된 fake인 $\tilde{Y}$와 실제 녹음 $Y$, $\hat{Y}$를 판별하는 discriminator $D$
  • 학습 안정성을 위해 L2 loss로 separator를 pretrian하고, source 당 하나씩 $k$개의 DCGAN-like discriminator를 train
    - $L^{real \_ unpair}_{k} = \frac{1}{4} ( D_{k}(\hat{Y}_{n,w,k})-0.9)^{2}$
    - $L^{real \_ pair}_{k} = \frac{1}{4} (D_{k}(Y_{n,w,k}) - 0.9)^{2}$
    - $L^{fake \_ unpair}_{k} = \frac{1}{4} (D_{k} (f(\hat{X}_{n,w})_{k}) - 0.1)^{2}$
    - $L^{fake \_ pair}_{k} = \frac{1}{4} (D_{k} (f(X_{n,w})_{k}) - 0.1)^{2}$
    - $L_{k} = L^{real \_ unpair}_{k} + L^{real \_ pair}_{k} + L^{fake \_ unpair}_{k} + L^{fake \_ pair}_{k}$
  • 각 반복마다 $L_{k}$ loss를 기반으로 각 disciminator $k$를 업데이트하고, $L_{adv}$ loss로 separator를 학습
    - $L_{sep} = \frac{1}{K} \sum_{k} (D_{k}(f(X_{n,w})_{k}) -0.9)^{2} + (D_{k}(f(\hat{X}_{n,w})_{k})-0.9)^{2}$
    - $L_{adv} = L2_{freq}+\gamma L_{sep}$

Adversarial Loss 구성

- Deep Feature Loss

• $J$ layer가 있는 nerual network $\Phi$를 통해 target $Y$와 추정된 magnitude spectrogram $\tilde{Y}$를 얻을 수 있음
  
  • $\Phi$가 미분가능하면 target audio embedding과 추정된 audio embedding 사이의 거리를 사용하여 $\Phi$의 모든 layer $j$에서 deep feature loss를 정의 가능
  • 이때, deep feature loss는 L2 distance를 기반으로 함
    - $L^{\Phi , j}_{feat} = \frac{1}{C_{j} H_{j} W_{j} K} \sum_{c,h,w,k} | \Phi_{j}(\tilde{Y}_{n,w,k}) - \Phi_{j}(Y_{n,w,k})|^{2}$
    - $C_{j} \times H_{j} \times W_{j}$ : 각 layer $j$의 embedding shape
  • 어떤 feature가 activate 되는지에 대한 정보를 캡처하는 style reconstruction loss를 활용할 수 있음
    - Gram Matrix $G^{\Phi (Y)}_{j} = \frac{\Psi_{Y} \Psi^{T}_{Y}} {C_{j} H_{j} W_{j} }$
    - $\Psi_{Y}$ : $C_{j} \times H_{j} \times W_{j}$로 reshape된 $Y$ embedding이고, $G^{\Phi (Y)}_{j}$는 $C_{j} \times C_{j}$ shape을 가짐
    - $L^{\Phi , j}_{sty} = \sum_{c, c} | G^{\Phi(\tilde{Y})}_{j} - G^{\Phi(Y)}_{j}|^{2}$
  • 실험을 위해 $\Phi$는 VGGish model을 사용하고 $L2_{freq}$ loss로 정규화된 deep feature loss를 사용
    - $L_{deep \_ feat} = L2_{freq} + \delta L^{\Phi , j} _{feat} + \lambda L^{\Phi , j}_{sty}$

3. Experiments

- Settings

• Dataset : MUSDB18 (보컬, 베이스, 드럼, 그 외에 대한 4가지 music source)
• Model : OpenUnmix 기준으로 개별적인 loss들 벤치마킹 평가 

OpenUnmix 구조

- Objective Evaluation

• SDR은 높을 수록 좋고 Loss 기반의 평가 지표는 낮을 수록 좋음
  • 공통적으로 $L1_{mask}$와 $L2_{mask}$의 성능이 가장 낮게 나타남
    - Mask가 mixture의 silent region에 대해 잘못 정의되어 있기 때문
  • $L1_{time}$, $L2_{time}$도 마찬가지로 나쁜 성능을 보인 반면, $SISDR_{time}$, $SDSDR_{time}$, $LOGL1_{time}$, $LOGL2_{time}$과 같은 다른 time-domain loss는 좋은 성능을 보임
    - Loss에 포함된 로그 압축이 mask-based model에서 발생하는 low-energy phase artifact를 감소시키기 때문

SDR 기반 분리 품질 평가 (높을수록 좋음)

• Scale-invariant loss와 $LOGL1$과 $LOGL2$에 기반한 변형 loss들이 time-domain과 spectrogram 신호 모두에서 효과적으로 사용될 수 있음
  • $SISDR_{freq}$, $LOGL1_{freq}$, $LOGL2_{freq}$와 같은 loss도 좋은 성능을 보임
  • $L2_{freq}$ loss는 adverasrial train과 phase-sensitive loss와 결합해서 사용했을때 효과적임
    - Deep feature loss와 결합했을 때는 분리 품질이 크게 개선되지 않음

Loss 기반 분리 품질 평가 (낮을수록 좋음)

- Subjective Evaluation

• $LOGL1_{freq}$, $LOGL1_{time}$, Adversarial Loss, $L2_{freq}$, $SISDR_{freq}$에 대한 MOS기반 주관적인 분리 품질 평가
  • $L2_{freq}$가 대체적으로 선호되는 경향

MOS 기반 주관적 분리 품질 평가

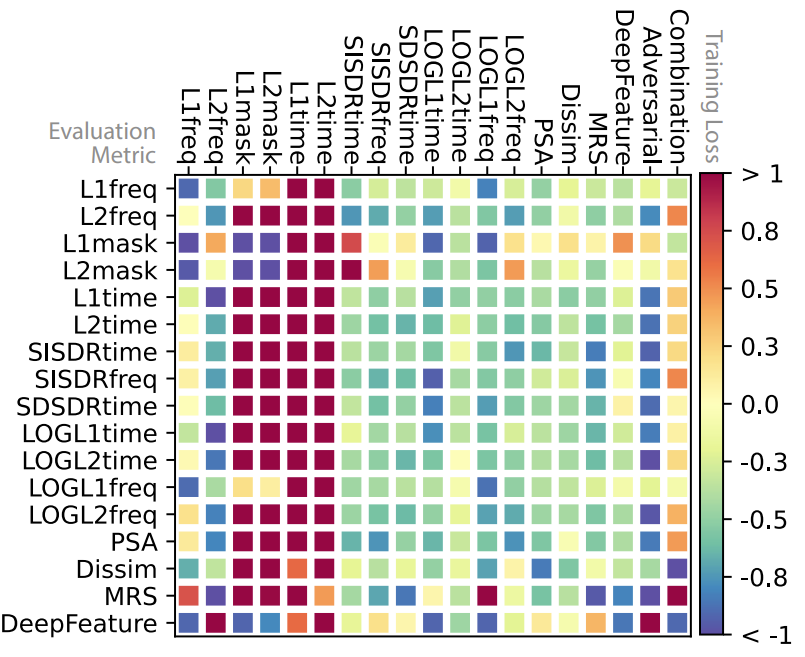
• 인간의 판단과 잘 연관되는 측정기준이 존재하는지 분석
  • $L1_{freq}$와 $SISDR_{freq}$와 같은 spectrogram based metric이 인간의 판단과 가장 높은 연관성을 보임

Loss 기반 metric과 MOS rating 사이의 상관관계 분석