[Paper 리뷰] Zen-NAS: A Zero-Shot NAS for High-Performance Image Recognition

Zen-NAS: A Zero-Shot NAS for High-Performance Image Recognition 

---

• Accuracy predictor는 Neural Architecture Search (NAS)의 핵심 구성요소
• 높은 성능의 accuracy predictor를 구현하려면 상당한 양의 계산이 필요함
• Zen-Score
  • Network expressivity를 나타내는 새로운 zero-shot index
  • 모델의 accuray와 양의 상관관계를 가짐
  • 학습된 network parameter 없이 무작위로 초기화된 network를 통해 few forward 추론만 수행
• Zen-NAS
  • Zen-Score를 기반으로 주어진 추론 예산하에서 target network의 Zen-Score를 최대화하는 NAS 알고리즘
• 논문 (ICCV 2021) : Paper Link
  • MAE-DET 논문도 읽어보면 좋음 (동일한 논문 저자)

---

1. Introduction

• NAS 알고리즘은 크게 architecture generator와 accuracy predictor로 구성됨
  • Generator는 가능성있는 고성능 network를 제안
    - Uniform sampling, Evolutionary algorithm, Reinforcement learning 등
  • Predictor는 제안된 network의 accuracy를 측정
    - Brute-force, Predictor-based method, One-shot method 등
• 높은 성능의 accuracy predictor를 구현하기 위해서는 막대한 계산 비용이 필요함
  • Brute-force와 Predictor-based method는 상당한 수의 network를 학습해야 함
  • One-shot method는 parameter sharing을 통해 계산 비용을 줄일 수 있음
    - BUT, 큰 supernet을 미리 구축해야 하므로 여전히 많은 계산 비용이 소모됨
    - Supernet 기반 방식은 model interfering으로 인해 accuracy predictor의 품질을 저하될 수 있음 

-> 그래서 zero-cost proxy인 Zen-Score를 제안

 

• Zen-Score는 deep neural network의 expressivity를 측정하고 모델의 accuracy와 양의 상관을 가짐
  • 무작위 Gaussian input을 사용해 무작위로 초기화된 network에서 few forward 추론만 수행함
    - Extremely fast, lightweight & data-free!
  • Zen-Score는 Batch Norm.으로 인해 발생하는 scale-sensitive 문제를 해결함
• Zen-Score를 기반으로 Zen-NAS 알고리즘을 설계함
  • 주어진 추론 예산하에서 target network의 Zen-Score를 최대화하는 방식
  • Zen-NAS는 search 과정에서 network parameter를 최적화하지 않는 zero-shot 방식

< Overall of Zen-Score & Zen-NAS >

• 효율적인 NAS를 위한 새로운 zero-shot proxy인 Zen-Score를 제안
  • Zen-Score는 효율적이고 Batch Norm.으로 발생하는 scale-sensitive에 민감하지 않다는 것을 증명
• Zen-Score를 기반으로 한 새로운 NAS 알고리즘인 Zen-NAS를 제안
  • Zen-NAS는 0.5 GPU day 만에 ImageNet에서 SOTA 성능을 달성

2. Expressivity of Vanilla Network

- Notations

• $L$-layer neural network : $f : \mathbb{R}^{m_{0}} \rightarrow \mathbb{R}^{m_{L}}$
  - $m_{0}$ : input dimension
  - $m_{L}$ : output dimension
  - $x_{0} \in \mathbb{R}^{m_{0}}$ : input image
  - $x_{t}$ : $t$-번째 layer의 output feature map
• $t$-번째 layer : $m_{t-1}$의 input channel과 $m_{t}$의 output channel을 가짐
  - $\theta_{t} \in \mathbb{R}^{m_{t} \times m_{t-1} \times k \times k}$ : convolution kernel
  - $H \times W$ : image resolution
  - $B$ : mini-batch size
• $N(\mu, \sigma^{2})$ : 평균 $\mu$, 분산 $\sigma^{2}$을 가지는 Gaussian Dist.

- Vanilla Convolutional Neural Network

• Vanilla Convolutional Neural Network (VCNN)
  • 여러 개의 convolution layer를 쌓아서 구성
  • 각 layer는 하나의 convolution operator와 ReLU activation으로 구성
  • Residual link, Batch Norm.을 포함한 다른 구성요소는 backbone에서 모두 제거됨
    1. Backbone 다음에는 Gloabal Average Pool (GAP)으로 feature map resolution을 $1 \times 1$로 줄임
    2. GAP 다음에는 fully-connected layer가 이어짐
    3. 마지막으로 soft-max를 통해 network ouput을 label prediction으로 변환
  • 입력 $x$와 network parameter $\theta$가 주어졌을 때, $f(x|\theta)$는 network backbone의 output을 나타냄
    - GAP layer 이전까지의 feature map을 의미 (pre-GAP layer)
    -> pre-GAP을 활용해 network expressivity를 측정
• 최신 network에서 사용되는 residual link, Batch Norm., self-attention 같은 보조 구조는 network의 representation power에 영향을 주지 않음
  • For example, 
    - Batch Norm.은 kernel fusion을 통한 convolutional kernel로 합쳐질 수 있음
    - Self-attention은 feature map의 선형 결합으로 볼 수 있음
  • 보조 구조는 network expressivity를 계산할 때 일시적으로 제거된 다음, train/test 단계에서 다시 추가됨
  • 위 수정 과정을 통해 대부분의 single-branch feed-forward network를 VCNN 구조로 변환 가능

- $\Phi$-Score as Proxy of Expressivity

• 주어진 VCNN $f(x|\theta)$의 expressivity에 대한 proxy로 $\Phi$-Score를 제안
  • VCNN은 activation 패턴에 따라 piece-wise linear function으로 분해할 수 있다는 것을 이용
  • (Lemma 1.) $t$-번째 layer에 대한 activation 패턴을 $A_{t}(x)$라고 했을 때, 모든 임의의 vanilla network $f(\cdot)$에 대해, $f(x|\theta) = \sum_{S_{i} \in S} \mathbb{I}_{x}(S_{i})W_{S_{i}}x$ 이다.
    - $S_{i}$ : $\{ A_{1}(x), A_{2}(x), ..., A_{L}(x) \}$을 따르는 convex polytope
    - $S$ : $\mathbb{R}^{m_{0}}$ 내 convex polytope의 유한 집합
    - $\mathbb{I}_{x}(S_{i})$ : $x \in S_{i}$ 이면 1, 그렇지 않으면 0
    - $W_{S_{i}}$ : size $\mathbb{R}^{m_{L} \times m_{0}}$의 coefficient matrix
  • 모든 vanilla network는 convex polytope $S = \{ S_{1}, S_{2}, ..., S_{|S|} \}$로 분할된 piece-wise linear function의 ensemble임 (by. Lemma 1.)
    - $|S|$ : linear-region의 개수
• Linear-region의 개수 $|S|$는 여러 연구에서 expressivity proxy로 사용되어 왔음
  • BUT, $|S|$에는 두 가지 제약이 존재
    1. 큰 network에서 $|S|$을 카운팅하는 것은 계산적으로 불가능함
       - 큰 network에서 linear-region의 수는 지수적으로 증가하기 때문
    2. Proxy에서 $W_{S_{i}}$의 representation power를 고려하지 않음
       - Linear classifier의 Gaussian complexity 때문
  • (Lemma 2.) Linear function $\{ f : f(X) = WX \textit{s.t}. \lvert W \rvert_{F} \leq G \}$에 대해, Gaussian complexity의 상한은 $O(G)$이다.
    - Gaussian complexity를 통해 얻어진 linear function의 expressivity는 parameter matrix $W$의 Frobenius norm에 의해 제어됨 (by. Lemma 2.)
• (Definition 1.) Lemma 1.과 Lemma 2.에 의해, Vanilla network $f(\cdot)$에 대한 Gaussian complexity는 아래와 같이 정의된다. 

VCNN의 $\Phi$-Score 정의

• VCNN의 expressivity ($\Phi$-Score) : Definition 1.의 식을 통해 얻어지는 Gaussian complexity 기댓값
  •  모든 VCNN은 linear function의 ensemble이므로, 각 linear-region에서 Guassian complexity를 평균하여 network expressivity를 계산할 수 있음
  • 사전 분포로부터 $x$와 $\theta$를 무작위 샘플링한 다음, $\lvert W \rvert_{F}$ 평균을 계산
    - input $X$에 대해 $f$의 gradient norm 기댓값을 구하는 것과 동일
    - $x$, $\theta$는 standard Gaussian dist. 로부터 샘플링됨
  • $\Phi$-Score는 $\theta$가 아닌 $x$의 graident만 포함
• 매우 깊은 vanilla network에서 $\Phi$-Score를 계산하면 gradient explosion이 발생하여 수치적 overflow가 발생함
  • Batch Norm.을 추가하면 gradient explosion을 해결할 수 있음
  • Scale-sensitive 문제 : Batch Norm.을 추가하면 $\Phi$-Score가 적응적으로 rescale 되므로 서로 다른 network 간의 $\Phi$-Score를 비교하기 어려움

-> Scale-sensitive 문제를 해결하고 Batch Norm.의 효과를 반영하는 재조정된 $\Phi$-Score가 필요

3. Zen-Score and Zen-NAS

- Overflow and BN-rescaling

• 매우 깊은 vanilla network에서 $\Phi$-Score를 계산하면 수치적 overflow가 발생
  • Batch Norm.이 network에서 제거되고 network output 규모가 depth에 따라 지수적으로 증가하기 때문
  • $P_{w/oBN}$과 $P_{BN}$ 간의 비교
    - $P_{w/oBN}$에서는 30 layer만 지나면 $\Phi$-Score의 overflow가 발생
    - $P_{BN}$처럼 Batch Norm.을 추가하면 overflow는 방지되지만, $\Phi$-Score의 값이 크게 축소됨
    -> BN-rescaling 현상
• BN-rescaling은 architecture ranking을 방해함
  • $Q_{w/oBN}$과 $Q_{BN}$ 간의 비교
    - Batch Norm.이 추가된 $Q_{BN}$은 모든 channel에서 거의 동일한 $\Phi$-Score를 가짐
    -> Architecture generator를 혼란시키고 잘못된 방향으로 search가 진행될 위험이 있음

BN-rescaling 현상에 대한 $\Phi$-Score 비교

- From $\Phi$-Score to Zen-Score

• $\Phi$-Score를 계산할 때 수치적 overflow를 방지하기 위해서는 Batch Norm.이 필요하지만 BN-rescaling이라는 부작용이 존재함
  • Batch Norm.이 있을 때 rescaling을 보정할 수 있는 Zen-Score를 설계
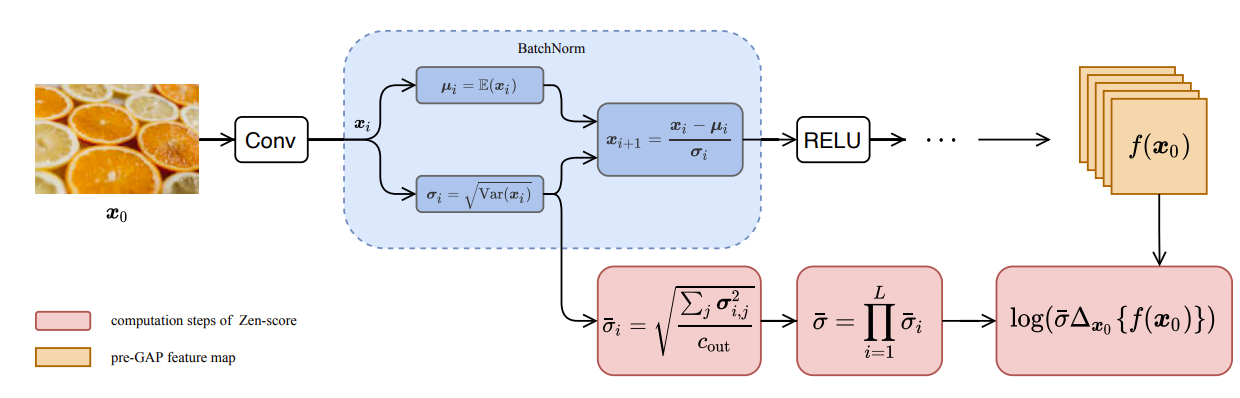
  • Zen-Score Algorithm
    1. 모든 residual link를 전처리를 통해 network에서 제거
    2. Input vector를 무작위로 샘플링하고 Gaussian noise를 추가
    - $\Delta$ : pre-GAP feature map의 perturbation
    - Backpropagation을 방지하기 위해 $x$의 gradient를 유한 차분 $\Delta$로 대체 
    3. Scaling factor $\overline{\sigma}^{2}_{i}$는 각 Batch Norm. channel의 분산으로 평균
    4. Zen-Score는 $\Delta$와 $\overline{\sigma}_{i}$의 log-sum으로 계산

Zen-Score 계산 알고리즘

• (Theorem 1.) $\overline{f}(x_{0}) = \tilde{x}_{L}$을 Batch Norm.이 없는 $L$-layer vanilla network, $f(x_{0}) = \tilde{x}_{L}$를 Batch Norm.이 있는 sister network라고 하자. $0 < \delta < 1, K_{0} \leq O[\sqrt{log(1/\delta)}]$에 대해 $BHW \geq O[(LK_{0})^{2}]$이 충분히 크고 적어도 $1-\delta$의 확률을 가지면,  $\epsilon \overset{\underset{\mathrm{\Delta}}{}}{=} O(2K_{0}/\sqrt{BHW})$ 일 때, 아래식을 얻는다. 

Theorem 1.으로 유도되는 식

• • Batch Norm.이 존재하는 network의 Zen-Score는 Batch Norm.이 없는 동일한 network의 $\Phi$-Score에 근사할 수 있음 (by. Theorem 1.)
  • Theorem 1. 은 $\lvert \overline{f}(\cdot) \rvert$를 계산하기 위해 $\lvert f(\cdot) \rvert$를 계산한 다음, $\prod_{t=1}^{L}\overline{\sigma}_{t}$로 rescaling 하는 것을 의미
    - Approximation error는 $L_{\epsilon}$으로 제한
  • $\overline{f}(\cdot)$과 $f(\cdot)$ 모두에서 $x$의 gradient를 취함으로써 Zen-Score와 $\Phi$-Score 사이의 관계를 얻을 수 있음

도식화된 Zen-Score 계산 과정

- Zen-NAS for Maximizing Expressivity

• Target network의 Zen-Score를 최대화하도록 Zen-NAS 알고리즘을 설계
  • Architecture generator로 Evolutionary Algorithm (EA) 사용
    - EA의 단순성 때문에 선정
  • Reinforcement learning, Greedy selection 등을 사용할 수도 있음
• Zen-NAS Algorithm
  1. N개의 structure를 무작위로 생성
  2. 각 반복 $t$ 마다 모집단 $P$에서 structure를 무작위로 선택하고 mutate
  - 선택된 layer의 width와 depth는 주어진 범위에 따라 mutate 됨
  3. 새로운 structure $\hat{F}_{t}$가 추론 예산을 초과하지 않는 경우, 모집단에 추가
  - Network의 최대 depth는 $L$에 의해 제어되며 지나치게 깊은 structure를 만드는 것을 방지
  4. Zen-Score가 가장 작은 network를 제거하여 모집단의 크기를 유지
  5. $T$ 반복 후 Zen-Score가 가장 큰 network가 Zen-NAS의 출력으로 반환됨
  - ZenNet : Zen-NAS로 얻어진 architecture 

Zen-NAS 알고리즘

4. Experiments

- Settings

• Dataset : CIFAR-10, CIFAR-100, ImageNet-1k
• Device : NVIDIA T4, Google Pixel2
• Search Space : ResNet, MobileNet

- Zen-Score vs. Other Zero-shot Proxies

• 5개 zero-shot proxy들과 비교 : FLOPs, Gradient-norm, Synflow, TE-Score, NASWOT
• Zen-Score가 다른 proxy들 보다 가장 좋은 성능을 보임

CIFAR-10, CIFAR-100에서의 비교

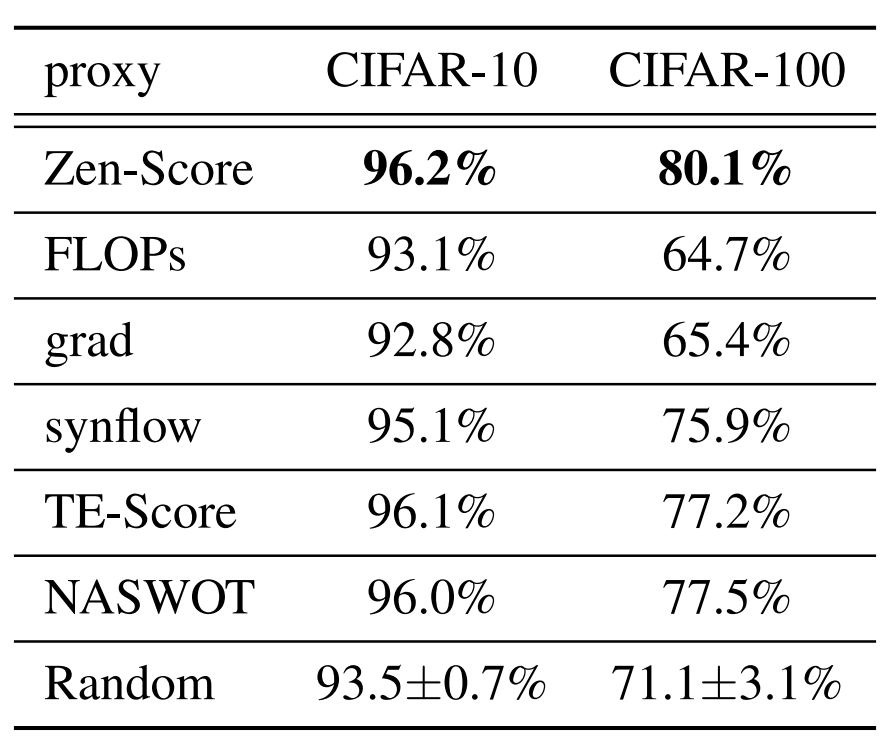
• Zen-Score의 계산 속도는 TE-Score보다 20~28배 빠름

ResNet에 대한 proxy 비교

- Zen-NAS on ImageNet

• ImageNet에서 Zen-NAS를 적용해 얻어진 network인 ZenNet에 대한 비교 실험을 수행
• Baseline
  - ResNet, DenseNet, ResNeSt, MobileNet-V2
  - OFANet (9ms / 11ms), DFNet, RegNet
  - OFANet (389M / 482M) / 595M, DNANet, EfficientNet, MnasNet
• ZenNet은 accuracy와 추론 속도 모두 크게 향상된 것을 보임
  - ZenNet은 EfficientNet과 비교했을 때 83.6%의 top-1 accuracy를 4.9배 더 빠르게 달설

ZenNet의 추론 Latency 비교

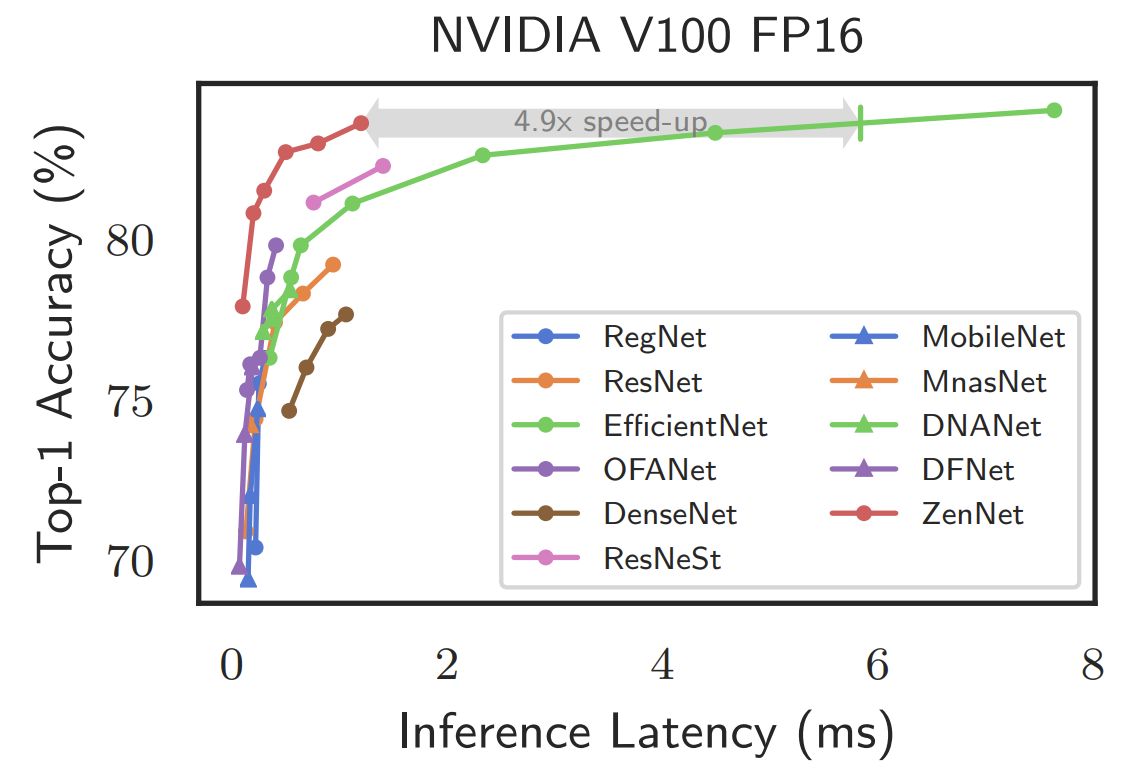
• ZenNet은 80.8%의 top-1 accuracy를 EfficientNet보다 43% 더 적은 FLOP만으로 달성

ZenNet의 FLOP 비교

- Searching Cost of Zen-NAS vs. SOTA

• 기존 NAS 방법은 최고 성능의 network를 얻는데 수백~수천 GPU day를 소모하고 대부분 80% 미만의 accuracy를 보임
• Zen-NAS는 0.5 GPU day 만에 83.6%의 top-1 accuracy를 달성
  - 비슷한 성능의 OFANet보다 100배 빠르고 EfficientNet보다 7800배 빠름

Zen-NAS vs. SOTA