[Paper 리뷰] MAE-DET: Revisiting Maximum Entropy Principle in Zero-Shot NAS for Efficient Object Detection

MAE-DET: Revisiting Maximum Entropy Principle in Zero-Shot NAS for Efficient Object Detection

---

• Object detection에서 backbone architecture의 추론 시간을 줄이기 위해 Nerual Architecture Search (NAS)를 도입
• 기존 NAS 방식은 GPU 및 시간 자원이 많이 필요하므로 빠른 연구 개발을 위해 Zero-shot NAS 방식을 제안
• MAE-DET
  • Maximun Entropy Principle을 통해 network parameter를 훈련시키지 않고 효율적인 detection backbone을 설계
  • Architecture desgin 비용은 zero에 가깝지만 SOTA의 성능을 발휘
  • Detection backbone의 Differential Entropy를 최대화하여 동일한 계산 제약 아래서 더 좋은 feature extractor로 기능
• 논문 (ICML 2022) : Paper Link
  • Zen-NAS 논문도 읽어보면 좋음 (동일한 논문 저자)

---

1. Introduction

• Object detection network는 feature extraction backbone에 크게 의존함
  • 현재 대부분의 SOTA detection backbone은 전문가에 의해서 수동으로 설계됨
  • Detection backbone은 많은 detection framework에서 전체 추론 비용의 절반 이상을 소비
  • 서버용 GPU, 모바일 등 다양한 하드웨어 플랫폼에서 최상의 speed-accuracy trade-off를 위해 backbone architecture를 최적화하는 것이 중요

• Detection task를 위한 기존의 NAS 방법들은 모두 training-based로 수행됨
  • 후보 network의 성능을 평가하기 위해서 parameter를 훈련시켜야 하므로 하드웨어 자원을 많이 소모함
  • 빠른 연구 및 개발을 비효율적으로 만드는 주요한 원인
  • Zero-shot NAS는 network parameter를 훈련시키지 않고 network의 성능을 예측하므로 training-based NAS보다 빠르게 동작

-> 그래서 효율적인 object detection backbone을 설계하기 위해 Zero-shot NAS를 도입

 

• Maximum Entropy Principle 아이디어의 활용
  • Maximum Entropy Principle과 Zero-shot NAS 간의 연결을 시도
    - 주어진 추론 예산 하에서 Entropy가 최대에 도달할 때 object detection을 위한 더 나은 feature extractor로 동작하도록 함
  • 고차원 공간의 deep feature에 대한 정확한 확률 분포를 얻기 어렵기 때문에 deep network에서 Entropy를 효과적으로 추정하기 어려움
    - Entropy의 정확한 계산을 위해 feature map 분산을 요구하는 Differential Entropy의 Gaussian 상한 추정
  • Object 크기는 데이터셋에 따라 다르고 균일하지 않기 때문에 서로 다른 scale의 object에 대한 정확한 deep feature를 얻기 어려움
    - Entropy 추정 과정에서 MSEP (Multi-Scale Entropy Prior)를 도입
  • Detection backbone의 Differential Entropy를 최대화하여 network parameter를 훈련하지 않고도 최적의 network depth와 width를 탐색

• Standard single-branch convolution block만을 사용해서 기존의 복잡하게 구축된 backbone 성능을 능가
• MAE-DET의 전체 계산은 detection backbone 하나에 대해 forward 추론만을 계산하므로 비용이 거의 0 

< Overall of MAE-DET (MAximum-Entropy DETection) >

• Zero-shot object dection NAS에서 Maximum Entropy Principle을 적용
• 기존 NAS 방식보다 최소 50배 빠른 속도를 달성
• MAE-DET는 여러 object detection benchmark dataset에서 SOTA 성능을 갖춤

2. Preliminary

- Continuous State Space of Deep Network

• $F(\cdot) : R^{d} \rightarrow R$ : 입력 이미지 $x \in R^{d}$를 해당 label $y \in R$에 매핑하는 network
  
  • Network topology : $G = (V, E)$
    - $V$ : neuron으로 구성된 vertex set
    - $E$ : neuron 간의 spike로 구성된 edge set
  • $h(v) \in R$, $h(e) \in R$ : 각각 임의의 $v \in V$, $e \in E$에 대해 vertex $v$, edge $e$에 부여된 값
• $S = \{h(v), h(e) : \forall v \in V, e \in E \}$ : network $F$의 continous state space 집합
• (목표) Maximum Entropy Principle에 따라 주어진 계산 제약 하에서 network $F$의 Differential Entropy를 최대화하는 것
  • $H(S)$ : 집합 $S$에 대해 network $F$에 포함된 전체 정보의 Entropy
    - $H(S_{v}) = \{ h(v) : v \in V \}$ : Latent feature 정보
    - $H(S_{e}) = \{ h(e) : e \in E \}$ : Network parameters
  • Detection backbone 설계 시 network parameter $H(S_{e})$ 보다 latent feature $H(S_{v})$의 Entropy에만 관심 있음
    - $H(S_{v})$는 $F$의 feature representation 능력을 측정
    - $H(S_{e})$는 $F$의 model complexity를 측정
  • $F$의 Differential Entropy는 $H(S_{v})$를 default로 사용

- Entropy of Gaussian Distribution

• Gaussian Dist.에서의 Differential Entropy
  • (가정) $x$는 Gaussian Dist. $N(\mu, \sigma^{2})$에서 sampling 됨
  • (Eq.1.) $x$의 Differential Entropy : $H^{*}(x) =  \frac {1}{2} log(2\pi) + \frac {1}{2} + H(x)$
    - $H(x) := log(\sigma)$
    - Gaussian Dist.의 Entropy는 분산에만 의존

- Gaussian Entropy Upper Bound

• 확률 분포 $P(S_{v})$는 고차원의 함수이기 때문에 정확한 Entropy를 계산하기 어려움
• (Theorem 1.) 평균 $\mu$, 분산 $\sigma^{2}$을 가지는 모든 연속형 분포 $P(x)$에 대해, 그것의 Differential Entropy는 $P(x)$가 Gaussian Dist. $N(\mu, \sigma^{2})$일 때 최대화된다.
• Theorem 1. 은 Differential Entropy가 동일한 평균과 분산을 가지는 Gaussian Dist. 에 의해 상한이 생긴다는 것을 의미
  - Feature map의 분산을 계산한 다음 Eq.1. 을 통해 Network Entropy $H(S_{v})$에 대한 추정값을 얻음
  - 이 추정값에 대해 Theorem 1. 에 의해서 network에 대한 Gaussian Entropy 상한을 얻음

- Vanilla Network Search Space

• Backbone에 대한 vanilla convolutional search space를 구성
• Vanilla network : 여러 개의 convolution layer를 스택하고 뒤에 ReLU activation을 추가한 것
  • Vanilla Network의 Forward 추론 : $x^{l} = \phi(h^{l}),h^{l} = W^{l} * x^{(l-1)}$
    - $l = 1, ... , D$
    - $D$개의 layer에 대한 weight : $W^{1}, ... , W^{D}$
    - $D$개의 layer에 대한 출력 feature map : $x^{1}, ... , x^{D}$
    - 입력 이미지 : $x^{0}$
    - ReLU activation : $\phi(\cdot)$
• Vanilla convolutional network의 구조는 매우 간단함
  • Residual link, Batch Norm., SE block, Self-attention 등의 사용을 backbone에서 고려할 수 있음
  • MAE-DET는 Residual link, Batch Norm만 기본적으로 사용해서 디자인의 단순성을 유지 (Simple is Better!)

3. Maximum Entropy Zero-Shot NAS for Object Detection

- Differential Entropy for Deep Network

• Deep network에 의해 생성된 최종 feature map에 대한 Differential Entropy 계산
  • 모든 parameter를 standard Gaussian Dist. $N(0, 1)$로 초기화
  • Standard Gaussian Noise로 채워진 이미지를 무작위로 생성하고 Forward 추론 수행
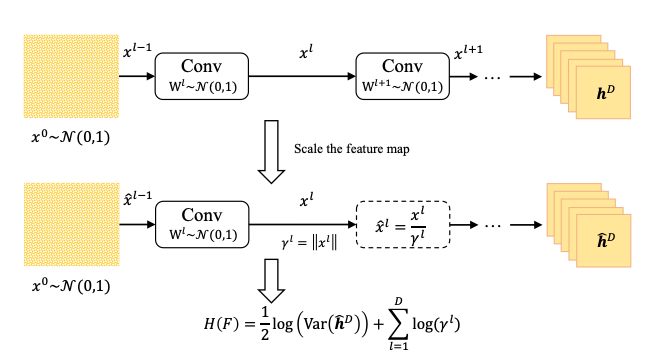
  • Network $F$에 대한 Gaussian 상한 Entropy : $H(F) = \frac{1}{2} log(Var(h^{D}))$
    - 분산은 마지막 pre-activation feature map $h^{D}$를 통해 계산됨
• Deep vanilla network의 경우 $H(F)$를 그대로 사용하면 모든 layer가 output norm을 크게 증폭하기 때문에 overflow가 발생
  
  • Feature map re-scale : $x^{l} = \phi(h^{l})/\gamma^{l}$
    - Batch Norm.을 대체해서 추론 중에 constant $\gamma^{l}$ 만큼 각 feature map $x^{l}$을 re-scale
  • 보정된 network의 Entropy : $H(F) = \frac{1}{2} log(Var(\hat{h^{D}})) +  \sum_{l=1}^{D}log(\gamma^{l})$
    - Forward 추론이 over/underflow 되지 않는 한에서 $\gamma^{l}$ 값은 임의로 주어질 수 있음
    - $\gamma^{l}$ 값을 feature map의 Euclidean norm으로 설정하면 잘 동작함
    - $H(F)$는 feature map에 대한 Entropy 추정을 위해 feature map 크기만큼 곱해짐

Rescaling을 적용한 Single-scale Entropy

- Multi-Scale Entropy Prior (MSEP) for Object Detection

• Real-world 이미지에서 object 크기는 균일하지 않음
  • Prior knowledge를 반영하기 위해 detection backbone은 5단계에 걸쳐 feature resoultion을 절반으로 downsampling
  • MSEP : 각 단계의 마지막 layer에서 feature map을 얻은 다음, 얻어진 feature map entropy들을 weighted-sum 하여 Multi-Scale Entropy를 구하는 과정

MSEP

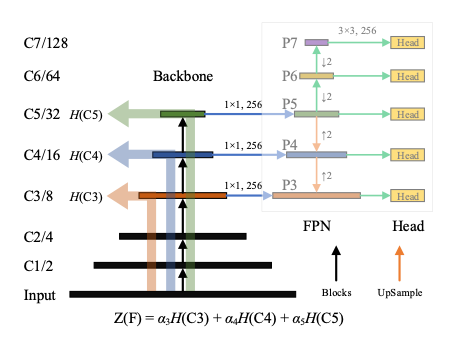
• Backbone $F$에 대한 Multi-Scale Entropy : $Z(F) := \alpha_{1}H(C1) + \alpha_{2}H(C2) + ... + \alpha_{5}H(C5)$
  • Backbone으로 추출된 multi-scale feature : $C = (C1, C2, ... , C5)$
  • FPN neck : Detection head에 대한 입력 feature $P = (P1, P2, ... , P7)$와 multi-scale feature $C$를 융합
  • $H(Ci)$ : $i = 1, 2, ... , 5$에 대한 $Ci$의 Entropy
  • 가중치 $\alpha = (\alpha1, \alpha2, ... , \alpha5)$ : 서로 다른 scale의 feautre expressivity 보정 전에 저장되는 Multi-Scale Entropy 값
  • $\alpha$ 값의 선택
    - $P3$, $P4$는 $P5$의 upsampling에 의해 생성, $P6$, $P7$은 $P5$의 downsampling에 의해 생성
    - $P5$는 $C5$에 의해 생성되고, $C5$는 object detection을 위해 다양한 scale에 대한 충분한 context를 가지고 있음
    -> $C5$의 역할이 가장 중요하므로 가중치 $\alpha5$를 큰 값으로 설정하는 것을 권장 : $\alpha = (0, 0, 1, 1, 6)$

- Evolutionary Algorithm for MAE-DET

• MAE-DET는 Evolutionary Algorithm (EA)를 사용하여 detection backbone의 Multi-Scale Differential Entropy를 최대화
• Search space를 점진적으로 줄이는 coarse-to-fine 전략 제안
  1. 모집단 $P$를 구성하기 위해 $N$개의 seed architecture를 무작위로 생성
     - Seed architecture $F_{t}$는 ResNet block, MobileNet block 등으로 구성
  2. 무작위로 하나의 block을 선택하고 mutate 버전으로 교체
  3. EA의 초기 반복에서 coarse-mutation을 사용하고, T/2 EA 반복 후에는 fine-mutation 사용
     - Coarse-mutation : block type, kernel size, width가 무작위로 mutate
     - Fine-mutation : kernel size, width만 무작위로 mutate
  4. Mutation 이후 새로 얻어진 $\hat{F_{t}}$의 추론 비용이 제약조건 (Latency, FLOP, depth $L$ 등) 보다 작으면 $\hat{F_{t}}$를 모집단 $P$에 추가
     - 최대 Depth 크기 $L$은 알고리즘이 높은 Entropy만을 가지는 비합리적으로 깊은 구조를 생성하는 것을 방지함 
  5. EA 반복 동안 모집단은 가장 작은 Multi-Scale Entropy를 가지는 최악의 후보를 제거하면서 크기를 유지
  6. 반복이 끝나면 Multi-Scale Entropy가 가장 높은 backbone 구조를 반환

Evolutionary Algorithm

4. Experiments

- Settings

• Datasets : COCO, VOC
• Inference Budget : ResNet-50/101

- Design Better ResNet-like Backbones

• MAE-DET-S는 ResNet-50 보다 60% 적은 FLOP 사용
• MAE-DET가 ResNet-50의 성능을 뛰어넘는 것으로 나타남
  • GFLV2 Head를 MAE-DET와 함께 사용하는 경우, COCO 데이터셋에서 mAP 2% 향상됨
  • 동일한 정확도를 기준으로 비교했을 때, MAE-DET는 ResNet-50보다 1.54배 빠른 추론 속도를 보임

MAE-DET vs ResNet

- Comparison with SOTA NAS methods

•  MAE-DET는 0.6 GPU days만을 사용하여 48%의 mAP를 달성
  -> 다른 NAS 방법들과 비교했을 때 50~100배 빠른 검색 속도를 보임
• DetNAS, SpineNet에 비해 MAE-DET가 더 적은 parameter를 요구하고 V100에서 더 빠른 추론 속도를 보임

MAE-DET와 다른 NAS method 간 성능 비교 1

MAE-DET와 다른 NAS method 간 성능 비교 2

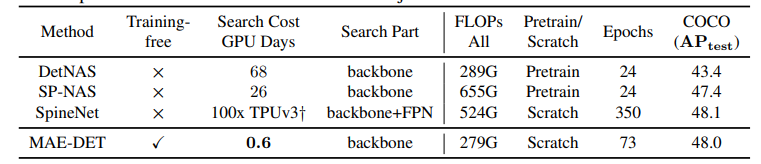
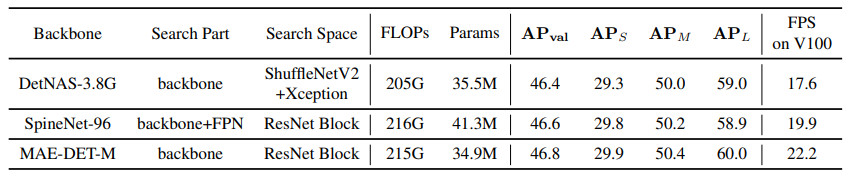
- Ablation Study and Analysis

• MAE-DET에 Single-Scale Entropy를 적용하는 경우
  • ResNet-50과 비교했을 때 0.7%의 Accuracy 향상
  • Zen-Score로 검색하는 경우 0.9%의 Accuracy 향상
• MAE-DET에 Multi-Scale Entropy를 적용하는 경우
  • Multi-Scale 방식이 Single-Scale 보다 COCO에서 0.3% mAP 향상
  • Coarse-to-fine Mutation 전략까지 사용하는 경우, Multi-Scale Entropy의 효과를 높임
    - ResNet-50과 비교했을 때, 1.1% Accuracy 향상

Single-scale, Multi-scale 성능 비교

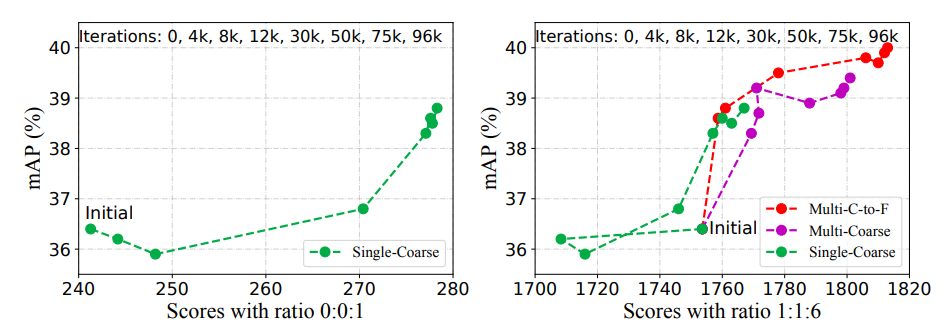
• mAP와 Multi-Scale Entropy는 양의 상관관계를 가짐
• Single-Scale Entropy는 mAP를 잘 표현하지 못하므로 Multi-Scale Entropy가 detection 작업에서 필요함

mAP와 Single-sclae, Multi-scale Entropy 간의 관계

- Transfer to Other Tasks

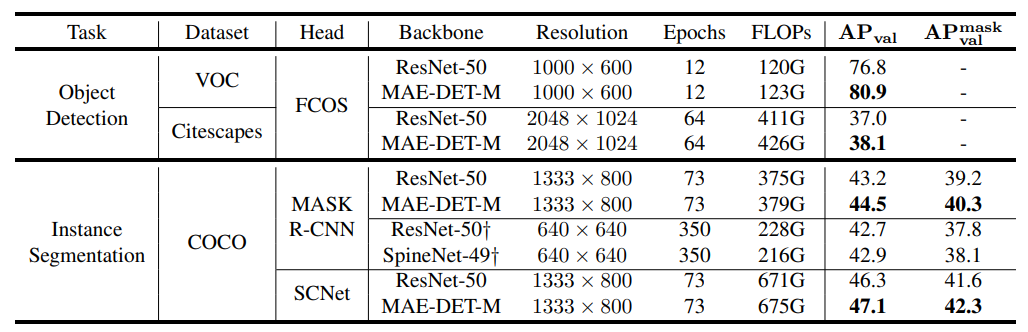
• VOC, Cityscapes : MAE-DET를 VOC, Cityscapes로 실험했을 때, ResNet 50과 비교하여 1.1%의 mAP 향상
• Instance Segmentation : COCO instance segmentation로 실험했을 때, ResNet-50과 비교하여 최대 1.3%의 mAP 향상

MAE-DET를 다른 task로 transfer 했을 때의 결과