티스토리 뷰
반응형
* Python을 기준으로 합니다
그래프 (Graph)
- 개념
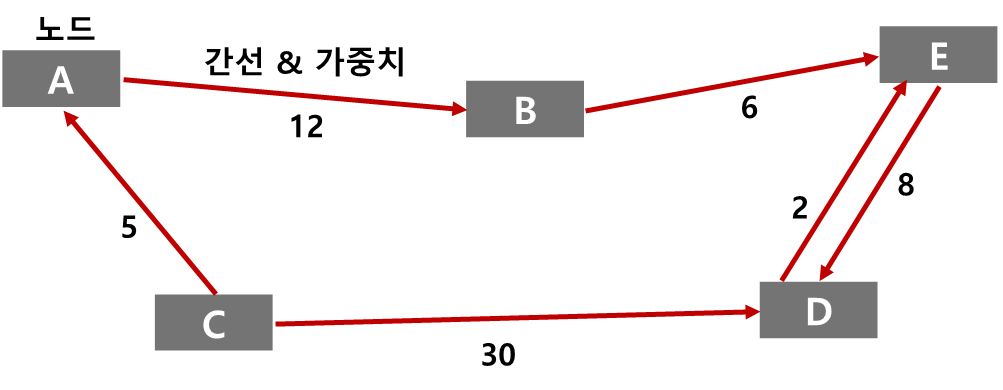
- 그래프 : 노드(Node)와 각 노드를 연결하는 간선(Edge)으로 구성된 비선형 자료구조
- 서로 연결되어 있는 객체를 다루는 경우 유용
- 일반적으로 그래프는 연결 조건에 제약이 없지만, 특정한 제약 조건을 가지는 경우 가중치를 통해 표현함
- 주요 용어
- 인접 (Adjacent) : 간선으로 연결된 두 노드를 adjacent 하다고 함
- 차수 (Degree) : 노드에 연결된 간선의 수
- 경로 (Path) : 간선을 따라 이동하는 경로
- 이때 경로를 구성하는 간선의 수를 경로 길이 (path length)라고 함
- 그래프의 종류
- 방향성에 따라
- 방향 그래프 (Directed Graph) : 두 노드를 연결하는 간선에 방향성이 존재하는 그래프
- 하나의 간선은 한 방향만을 가리키고, 노드 $A$에서 $B$로의 간선은 $<A,B>$, 노드 $B$에서 $A$로의 간선은 $<B,A>$로 표현
- $<A, B>$, $<B,A>$는 동일한 방향의 간선이 아님 - 무방향 그래프 (Undirected Graph) : 두 노드를 연결하는 간선에 방향성이 없는 그래프
- 하나의 간선은 양방향 모두를 가리키고, 이때 두 노드 $A, B$를 연결하는 간선은 $(A, B)$로 표현
- $(A, B)$, $(B,A)$는 동일한 간선을 의미
- 방향 그래프 (Directed Graph) : 두 노드를 연결하는 간선에 방향성이 존재하는 그래프
- 순환에 따라
- 순환 그래프 (Cycle Graph) : 특정 노드에서 간선을 따라 다시 돌아오는 경로가 있는 그래프
- 비순환 그래프 (Acyclic Graph) : 순환이 없는 그래프
- 간선 존재에 따라
- 완전 그래프 (Complete Graph) : 모든 노드 사이에 간선이 존재하는 그래프
- $n$개의 노드를 가지는 무방향 그래프는 $\frac{n(n-1)}{2}$개의 간선을 가짐
- $n$개의 노드를 가지는 방향 그래프는 $n(n-1)$개의 간선을 가짐 - 부분 그래프 (Sub Graph) : 간선을 일부만 가지는 그래프
- 완전 그래프 (Complete Graph) : 모든 노드 사이에 간선이 존재하는 그래프
- 가중치 그래프 (Weighted Graph) : 간선에 가중치가 할당된 그래프
- 방향성에 따라
- 구현
1. 인접 행렬 (Adjacency Matrix)
- 인접 행렬 : 2D 배열을 사용하는 방식
- 배열의 index는 노드, 배열의 값은 노드의 가중치로 두고 그래프를 표현하는 방식
- 간선이 존재하면 배열의 해당 성분에 가중치(무방향의 경우 1)를 표시하고, 존재하지 않으면 0으로 표현
`graph = [[0,400,100], [0,0,0], [500,0,0]]` - 노드 수를 $V$라고 했을 때 간선 정보를 저장하기 위해서 $O(V^{2})$ 만큼의 메모리가 필요하지만, 간선 비용을 $O(1)$의 시간으로 조회할 수 있음
- 즉, 조회의 time complexity는 좋지만 메모리 공간을 크게 소모 - 무방향 그래프에서는 인접 행렬은 항상 대칭행렬로 나타남
- 이 경우, 삼각 행렬만 저장함으로써 메모리 문제를 해결할 수 있음
- 배열의 index는 노드, 배열의 값은 노드의 가중치로 두고 그래프를 표현하는 방식

2. 인접 리스트 (Adjacency List)
- 인접 리스트 : 연결 리스트를 사용하는 방식
- 노드, 가중치, 다음 노드에 대한 정보를 연결 리스트로 만들어 나타내는 방식
- 노드 개수만큼 배열을 만든 다음,
`graph = [[] for _ in range(n+1)]` - 배열의 index는 각 시작 노드를 나타내고, 배열의 값에는 연결 리스트를 사용하여 다음 노드를 연결함
`graph[e[0]].append(e[1])`
- 노드 개수만큼 배열을 만든 다음,
- 간선 수를 $E$라고 했을 때 그래프를 나타내기 위해서 $O(E)$ 만큼의 메모리가 필요하고, 간선 비용 조회 시에는 $O(V)$ 만큼의 시간이 소모됨
- 즉, 조회 시 time complexity는 소모되지만 메모리를 효율적으로 사용할 수 있음
- 노드, 가중치, 다음 노드에 대한 정보를 연결 리스트로 만들어 나타내는 방식

import collections
graph = [[(1,30)], [(0,60),(2,50)],[(1,10),(3,70)],[(3,80),(0,20)]]
adj_list = collections.defaultdict(list) #인접리스트 방식 그래프
for idx, v in enumerate(graph):
adj_list[idx].append(v)
print(adj_list)
'''
{0: [[(1, 30)]],
1: [[(0, 60), (2, 50)]],
2: [[(1, 10), (3, 70)]],
3: [[(3, 80), (0, 20)]]})
'''3. 인접 행렬 vs. 인접 리스트
- 일반적으로 인접 행렬이 조회가 빠르고 구현이 쉽다는 장점이 있고, 완전 그래프에 가까운 대부분의 dense graph에도 적합
- 한편 메모리 공간이 적거나 정점에 비해 간선이 적은 희소 그래프 (sparse graph)의 경우 인접 리스트를 활용하는 것이 좋음
반응형
'Algorithm' 카테고리의 다른 글
| [Algorithm] 트라이 (0) | 2024.03.28 |
|---|---|
| [Algorithm] 트리 (0) | 2024.03.26 |
| [Algorithm] 해시 테이블 (0) | 2024.03.24 |
| [Algorithm] 큐, 덱 (0) | 2024.03.22 |
| [Algorithm] 스택 (0) | 2024.03.21 |
댓글

