티스토리 뷰
반응형
* Python을 기준으로 합니다
슬라이딩 윈도우 (Sliding Window)
- 개념
- 슬라이딩 윈도우 : 고정 크기의 윈도우가 이동하면서 윈도우 내의 데이터를 이용해 문제를 해결하는 방법
- 투 포인터와 비슷하지만 슬라이딩 윈도우는 정렬 여부에 관계없이 사용 가능함
- 구간 합 계산에 주로 활용 - Time complexity 측면에서 슬라이딩 윈도우는, 투 포인터와 마찬가지로 $O(n^{2})$ 이상 소모되는 배열 탐색을 $O(n)$ 내에 해결 가능함
- 투 포인터와 비슷하지만 슬라이딩 윈도우는 정렬 여부에 관계없이 사용 가능함

- 구현
1. 슬라이딩 윈도우 움직이기
- 배열에서 고정 크기만큼의 데이터를 가져오기 위해서 slicing을 활용함
def sliding_window(arr, window_size):
slide = []
for i in range(len(arr)-window_size+1):
slide.append(arr[i:i+window_size]) #slicing 활용
return slide
test = [1,9,3,2,4,5,7,8,6]
slide = sliding_window(test, 3) #3칸의 고정 size로 이동
for sl in slide:
print(sl, end=' -> ')
print('end')
#[1, 9, 3] -> [9, 3, 2] -> [3, 2, 4] -> [2, 4, 5] -> [4, 5, 7] -> [5, 7, 8] -> [7, 8, 6] -> end2. 슬라이딩 윈도우를 활용한 구간 합 계산
- 구간 합 계산은 prefix sum 기법을 활용하여 빠르게 계산할 수 있음
- 주어진 각 수들에 대해 prefix sum을 계산하여 새로운 배열 $P$로 저장
- 이때 해당 배열에 대한 구간 합은:
- 1차원 배열일 때 $X$에서 $Y$ 까지의 합:
$S = P[Y]-P[X-1]$
- 2차원 배열일 때 $(X1, Y1)$에서 $(X2, Y2)$ 구간에 대한 합:
$S = P[X2][Y2] - P[X1-1][Y2] - P[X2][Y1-1] + P[X1-1][Y1-1]$
def prefix_sum(arr, left, right):
pre_sum = 0
p = [0]
for i in arr:
pre_sum += i
p.append(pre_sum)
return p[right] - p[left-1]
test = [1,9,3,2,4,5,7,8,6]
print(prefix_sum(test, 3, 5)) #3~5번째 수들의 합 (3+2+4 = 9)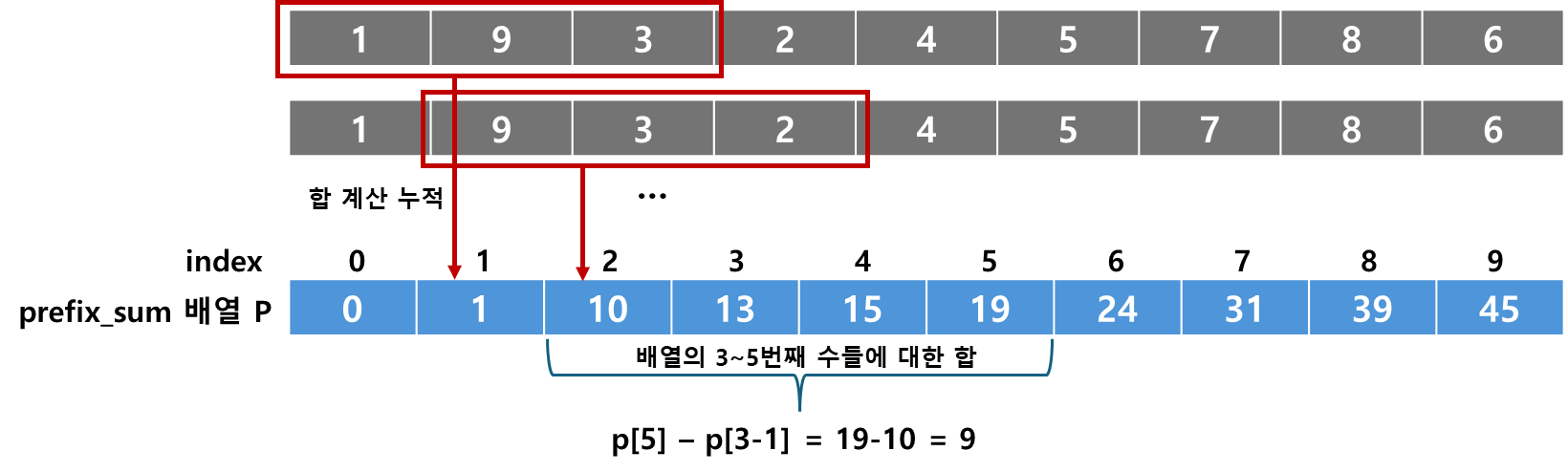
반응형
'Algorithm' 카테고리의 다른 글
| [Algorithm] 완전 탐색 (0) | 2024.04.05 |
|---|---|
| [Algorithm] 정렬 (0) | 2024.04.04 |
| [Algorithm] 투 포인터 (0) | 2024.04.01 |
| [Algorithm] 유니온 파인드, 서로소 집합 (0) | 2024.03.31 |
| [Algorithm] 우선순위 큐 (0) | 2024.03.30 |
댓글

