티스토리 뷰
반응형
* Python을 기준으로 합니다
유니온 파인드 (Union Find), 서로소 집합 (Disjoint Set)
- 개념
- 집합 : 순서와 중복이 없는 원소들을 가지는 자료구조
- 유니온 파인드 (=서로소 집합) : 교집합이 없는 두 집합 관계를 의미
- 해당하는 원소가 그래프에 연결되어 있는지를 판별하기 위한 자료구조로써, 일반적으로 트리를 통해 구현함
- 노드의 개수가 $V$이고 $V-1$개의 union 연산과 $M$개의 find 연산이 가능할 때, 유니온 파인드의 time complexity는 $O(V+M(1+\log_{2-M/V}V))$
- 유니온 파인드의 연산
- Find : 특정 노드의 root를 확인하는 연산 (노드가 같은 트리에 연결되어 있는지를 판별)
- 현재 노드의 parent를 찾는다
- Parent가 root이면 Find 연산을 종료하고, 아니면 반복한다
- Union : 두 집합이 동일한 root를 가지도록 하는 연산 (새로운 노드를 트리에 추가하는 것과 동일)
- 두 집합에서 각각의 root를 찾는다 (Find)
- A 트리의 root를 B 트리의 root로 설정한다
- 일반적으로 더 큰 root가 더 작은 root를 가리키도록 설정함
- Find : 특정 노드의 root를 확인하는 연산 (노드가 같은 트리에 연결되어 있는지를 판별)
- 구현
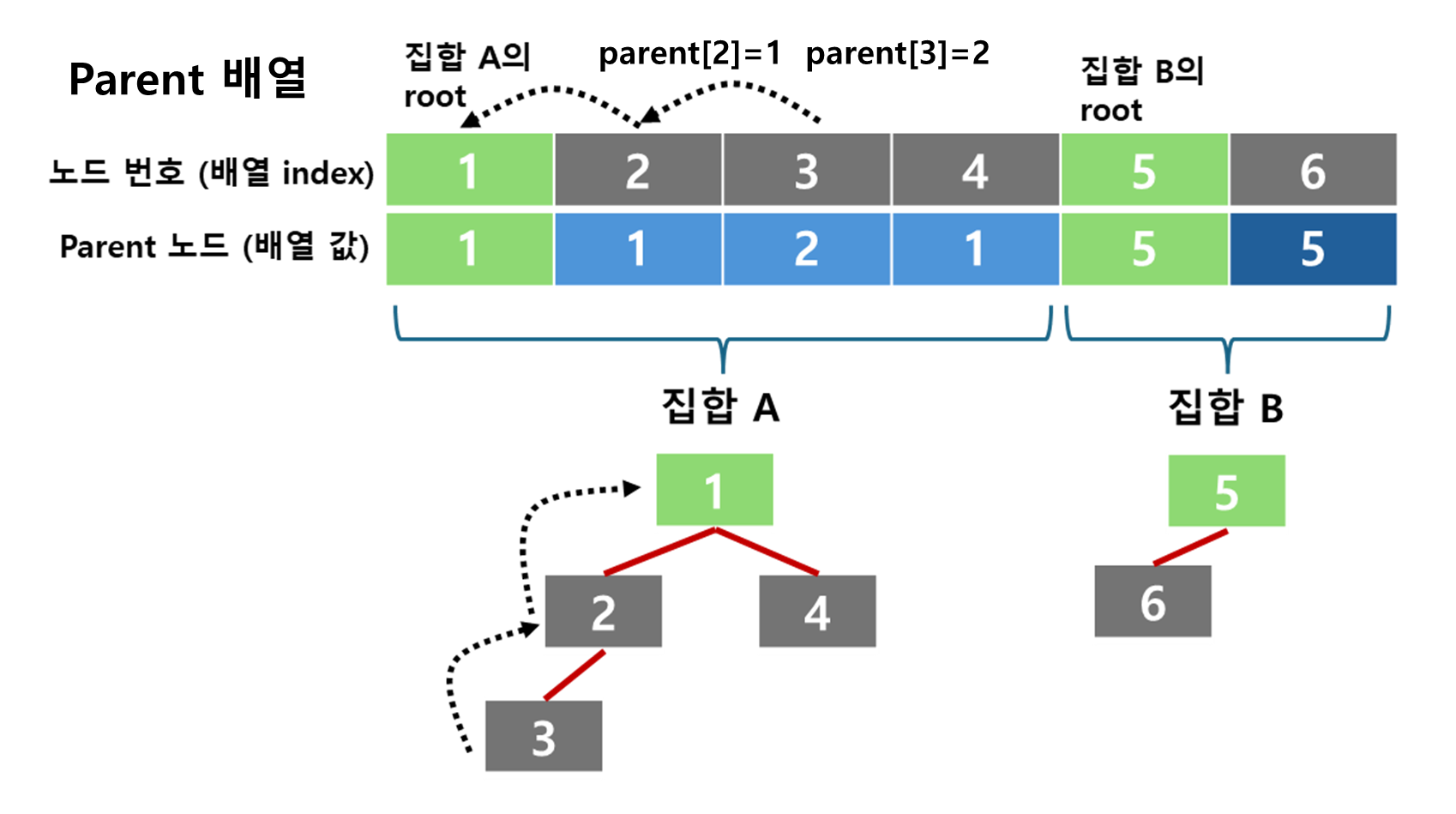
1. 배열 기반 트리를 사용한 집합의 표현
- 유니온 파인드는 배열 기반의 트리를 통해 구현됨
- 이때 배열의 index는 자기 자신을 나타내고, 배열의 값은 parent를 나타냄 (이때, root는 값과 index가 동일함)
- ex) `parent[3] = 2` : 노드 3의 parent는 2
2. Find 연산
- Find 연산은 root 노드를 찾는 연산으로 일반적으로 재귀 호출로써 구현되지만, 최악의 경우 $O(N)$의 time complexity를 가질 수 있음
def find(parent, x):
if parent[x] == x: #root이면
return x
#root가 아니면 재귀적으로 find 수행
return find(parent, parent(x))- 이때 경로 압축 (Path Compression)을 사용하면 Find 연산의 time complexity를 줄일 수 있음
def find(parent, x):
if parent[x] == x: #root 노드이면
return x
#경로압축
parent[x] = find(parent,parent[x]) #find를 재귀호출하고, parent table의 값을 갱신하는 방식
return parent[x]3. Union 연산
- Union 연산은 두 집합의 root 노드를 연결하는 연산
def union(parent, x, y):
x = find(parent, x)
y = find(parent, y)
if x == y: #두 집합이 이미 연결되어 있으면
return #union하지 않음
#연결되지 않았으면
if x < y: #더 작은 값을 root로 union함
parent[y] = x
else:
parent[x] = y- 유니온 파인드 결과 확인
parent = [0]*7
for i in range(1, 7): #parent table 초기화
parent[i] = i
graph = [[1, 4], [2, 3], [2, 4], [5, 6]]
for x, y in graph:
union(parent, x, y) #union
for i in range(1, 7): #find - 각 node의 root 찾기
print(find(parent, i), end=' ') # 1 1 1 1 5 54. 유니온 파인드를 활용한 그래프 내 Cycle의 판별
- 유니온 파인드를 사용해서 무향 그래프에서 cycle 여부를 판별할 수 있음
- 두 노드의 root를 find 했을 때, 같다면 cycle이 존재하는 것이므로 연산을 종료
- cycle이 존재하지 않는다면 (두 노드의 root가 다르면), union을 수행
- 위 과정을 반복
parent = [0]*7
for i in range(1, 7): #parent table 초기화
parent[i] = i
graph = [[1,2],[1,3],[2,3]] #cycle이 있는 무향 graph
for a,b in graph:
if find(parent, a) == find(parent,b): #find했을때 root가 같으면
print('CYCLE!') #cycle!
break
else: #root가 다르면
union(parent, a, b) #union
반응형
'Algorithm' 카테고리의 다른 글
| [Algorithm] 슬라이딩 윈도우 (0) | 2024.04.02 |
|---|---|
| [Algorithm] 투 포인터 (0) | 2024.04.01 |
| [Algorithm] 우선순위 큐 (0) | 2024.03.30 |
| [Algorithm] 힙 (0) | 2024.03.29 |
| [Algorithm] 트라이 (0) | 2024.03.28 |
댓글

